Matlab实现液态分子动力学实例演示

过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载,**:927550334
![]()
过冷水在往期的文章中《过冷水:分子动力学数据的Matlab处理程序设计》有给大家演示过对一个体系做动力,过冷水实例演示了粒子是如何运动的。当时分子运动的数据是做动力学得到了一些列坐标数据。
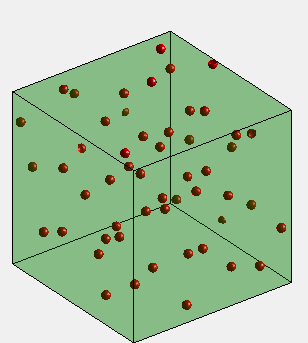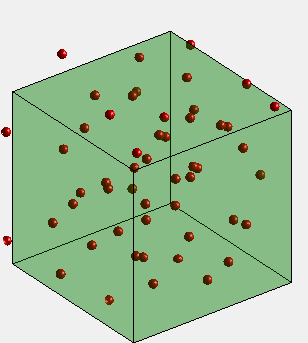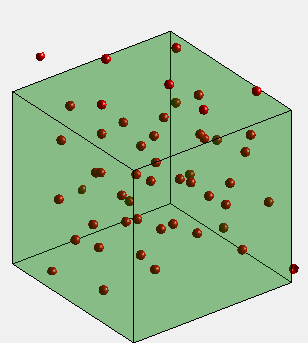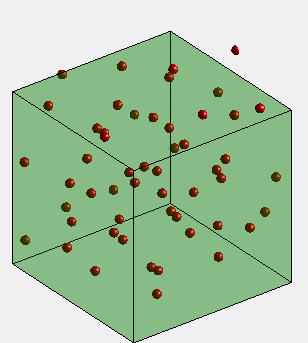
在实验模拟中模拟对象的受力情况和运动轨迹是常规的研究内容,本期过冷水就和大家一起学习如何用Matlab实验简单的研究对象的动力学模拟。
对于分子体系,理论和实验结合证明分子的运动规律服从经典力学, Hobenberg-Kohn第一定理证明分子体系的微观状态取决于分子核骨架的几何结构,分子微观状态的时间演化,就是核骨架几何结构随着时间的变化.既然分子体系中原子核的运动服从经典力学,那么就可以用牛顿力学描述分子运动。
对于原子层次模拟,不存在与粒子速度有关的非保守力。根据经典力学,力Fi取决于分子所受势能U, 势能U关于体系第i个核位置的负梯度就是第i个原子核所感受的力。
学习过初中物理的就知道知道只要知道受力,分子就运动起来了,分子动力学(MD,molecular dynamics)理论模拟可以包括三步:
第一步求体系的总势能U;第二步从总势能求算每个分子受力F,
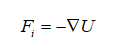
第二步求算每个分子位置随时间变化;
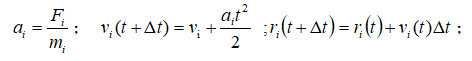
第三步求算体系任意动力学量,即所有物理化学性质。
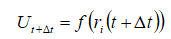
用力场方法求算势能,特别是在目前计算机能力还不够强的情况下,绝大多数分子动力学模拟中求算势能的一步几乎都是用力场方法完成的。分子动力学处理分子体系是一种动态研究的方法,它依据经典力学求解核骨架的行为。在上述求解动力学过程中,需要求解常微分方程,在动力中最开始并且使用较多的方法是Verlet法,
1967年问世的 Verlet法开创了用于分子动力学模拟中最重要的一类算法.设t时刻第i号粒子的位置、速度、加速度和位置关于时间的三阶导数分别为ri (t), vi (t):(t),ai (t)和bi (t).根据Newton定理,保守系中第i号粒子加速度可以从它受到的力Fi (t)求得,而力从势能的负梯度求得
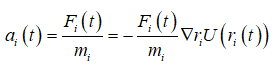
令∆t为模拟的时间步长,将ri(t ∆t), ri(t-∆t),分别在t时刻作Taylor展开到三阶项

和
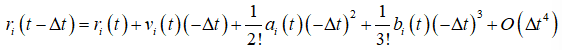
两式相加可以消去奇次导数项,得到
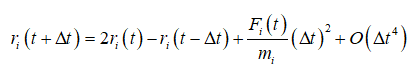
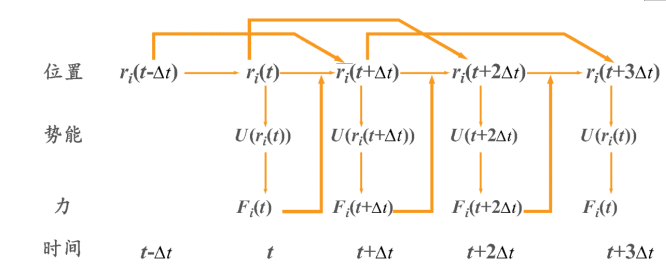
这就是Verlet法基本方程. 这是一个递推的关系式,只要有了起始条件,如{ri (0),ri(∆t)},就可以按照图所示的 Verlet法示意图求得以后所有时刻体系所有粒子的位置{ri (t)},即体系核骨架的时间演化, 其中,时间步长∆t总是选为定值. Verlet法是分子动力学中采用最普遍的算法,优点之一是时间可逆.式是由ri(t △t), ri(t △t)分别一前一后在t时刻展开得来的,由此可以看出式满足时间可逆,而时间可逆是Newton方程的基本要求, Verlet法的每一步只需计算一次力,这是优点之二,位置及其误差:微分方程用差分来求,于是计算误差来自Taylor 展开.在求位置的式中弃去的项是O (∆t4),故Verlet法计算位置的误差为O (Ot).
根据上述计算流程理论上可以计算分子运动轨迹,还需要注意的是分子体系势能计算。液态体系中最常见的是使用双体势来计算分子的势能。
双体势能
双体势ε(r)是指液态中两近邻原子之间势能。平衡态液体所有性质本质上都是由ε(r)决定的。原则上可以用量子力学来推导ε(r),但由于计算量巨大,除一些最简单的原子如H和He以外,用量子力学方法来计算双体势本ε(r)尚未做到。实际的数值计算中,通常采用简化的双体势的经验模型。
(a)硬球势
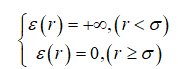
(b)负指数势
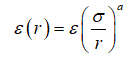
(c) Lennard-Jones 势能
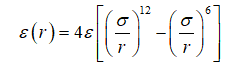
(d)有效离子-离子作用势
通常有效离子-离子作用势来表示液态金属原子间的双体势:
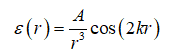
离子势假定液态金属中,由于传导电子作用,存在着长程振动交互作用,并由此建立模型。

过冷水在实际工作中会使用Lennard-Jones势,有效离子-离子作用势.硬球势和负指数势实在是太简单了,实际工作中应用案例不高。解决了对势的问题,则就可以计算动力学了
具体实现程序
先做一百个分子的体积,定义体系长宽高
MASS = 1;%原子质量 KB = 1;%玻尔兹曼常数 TEMPERATURE = 1.5;%温度 NUM_ATOMS = 100;%原子数 Density=0.5; % 体系数密度 LENGTH = power(NUM_ATOMS/Density,1.0/3.0); %体系长宽高 TSTEP = 1e-3;%时间步长Δt SIM_NO = 500000;动力学运动步数 EPS = 1.0; SIG = 1.0; R_CUT = 2.5*SIG; POT_E = 0.0; KIN_E = 0.0; TOT_E = 0.0;
% 原子位置,速度,力位置 POSITION = zeros(NUM_ATOMS,3); VELOCITY = zeros(NUM_ATOMS,3); FORCE = zeros(NUM_ATOMS,3); Number=NUM_PER_DIM; Lat_Const = LENGTH /(Number 2.0); Nplace=1; for(i=1:Number) for(j=1:Number) for(k=1:Number) if(Nplace<=NUM_ATOMS) POSITION(Nplace,1)= i*Lat_Const; POSITION(Nplace,2)= j*Lat_Const; POSITION(Nplace,3)= k*Lat_Const; end Nplace = Nplace 1; end end end
上述过程就完成了初始值的设置。计算第一步的力,要计算力就需要计算势能和势能的偏导,势能选择Lennard-Jones势,需要注意Lennard-Jones给出的只是两两原子间势能,我们需要的是作用在具体一个分子上的所有势能应该是对势的和,同样的道理,力也是多个分子相互作用受力之和。
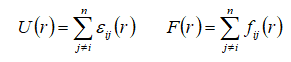
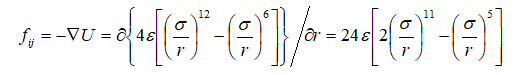
dr = zeros(3,1); FORCE(:) = 0.0; POT_E = 0.0; for ( i=1:NUM_ATOMS ) for ( j=i 1:NUM_ATOMS ) dist2 = 0.0; %计算两个分子之间的两两距离 for(k = 1:3) dr(k) = POSITION(i,k) - POSITION(j,k); %添加周期性边界条件判据 if(dr(k) > LENGTH/2.0) dr(k) = dr(k) - LENGTH; end if(dr(k) < -LENGTH/2.0) dr(k) = dr(k) LENGTH; end dist2 = dist2 dr(k)*dr(k); % dist2 IS BASED UPON MIC end if(dist2 <= R_CUT*R_CUT) % IF THE CUT OFF CRITERIA IS SATISFIED dist2i = power(SIG,2)/dist2; dist6i = power(dist2i,3); dist12i = power(dist6i,2); POT_E = POT_E 4.0 * EPS * (dist12i - dist6i); % 势能 Ff = 24.0 * EPS * (2*dist12i-dist6i); Ff = Ff * dist2i;%受力 for(k = 1:3) FORCE(i,k) = FORCE(i,k) Ff*dr(k); FORCE(j,k) = FORCE(j,k) - Ff*dr(k); end end end end
读者看到这里是不是觉得分子动力怎么这么简单,这里需要注意的是我们给出了简化的势能函数使得力的计算很容易,实际在Verlet中根据对势求力是采用差分法计算的,而不是直接求偏导。在知道力的基础上就可以求速度和位移。
old_force = FORCE; %上一步分子的受力 for(i = 1:NUM_ATOMS) for(j = 1:3) POSITION(i,j)=POSITION(i,j) VELOCITY(i,j)*TSTEP 0.5*FORCE(i,j)*TSTEP*TSTEP/MASS; 求下一步的位置 %做位置周期性判断 if(POSITION(i,j) > LENGTH) POSITION(i,j) = POSITION(i,j) - LENGTH; end if(POSITION(i,j) < 0.0) POSITION(i,j) = POSITION(i,j) LENGTH; end end end %计算新的位置下的力 for ( i=1:NUM_ATOMS ) for ( j=i 1:NUM_ATOMS ) dist2 = 0.0; %计算两个分子之间的两两距离 for(k = 1:3) dr(k) = POSITION(i,k) - POSITION(j,k); %添加周期性边界条件判据 if(dr(k) > LENGTH/2.0) dr(k) = dr(k) - LENGTH; end if(dr(k) < -LENGTH/2.0) dr(k) = dr(k) LENGTH; end dist2 = dist2 dr(k)*dr(k); % dist2 IS BASED UPON MIC end if(dist2 <= R_CUT*R_CUT) % IF THE CUT OFF CRITERIA IS SATISFIED dist2i = power(SIG,2)/dist2; dist6i = power(dist2i,3); dist12i = power(dist6i,2); POT_E = POT_E 4.0 * EPS * (dist12i - dist6i); % 势能 Ff = 24.0 * EPS * (2*dist12i-dist6i); Ff = Ff * dist2i;%受力 for(k = 1:3) FORCE(i,k) = FORCE(i,k) Ff*dr(k); FORCE(j,k) = FORCE(j,k) - Ff*dr(k); end end end End %计算分子相应位置下的动能 KIN_E = 0.0; for(i = 1:NUM_ATOMS) for(j = 1:3) VELOCITY(i,j)=VELOCITY(i,j) 0.5*(FORCE(i,j) old_force(i,j))*TSTEP/MASS; KIN_E = KIN_E 0.5*power(VELOCITY(i,j),2); end
上述程序完整的实现力分子动力的计算
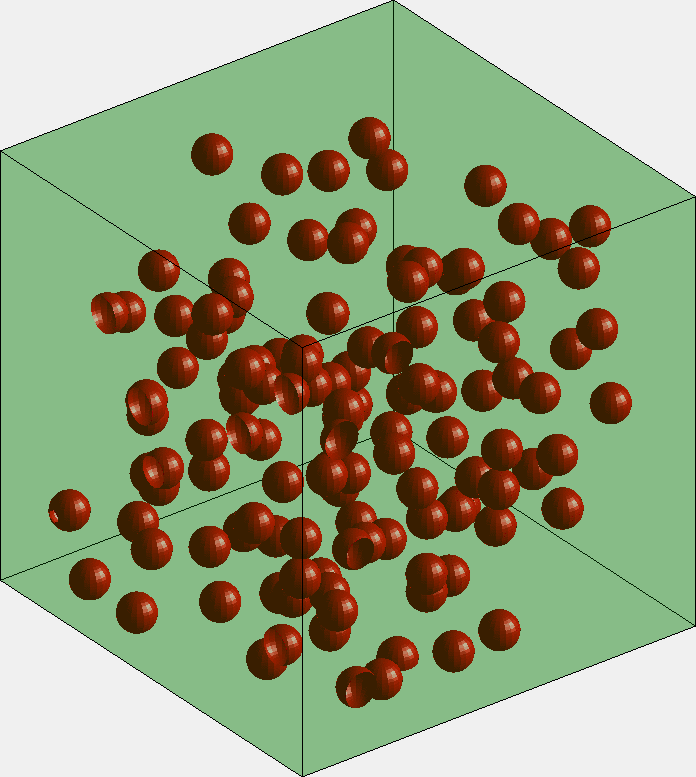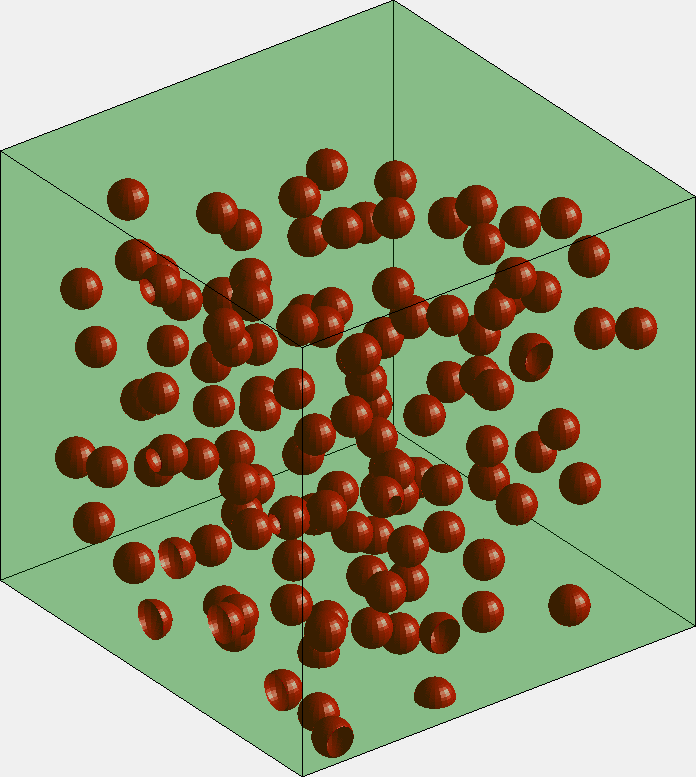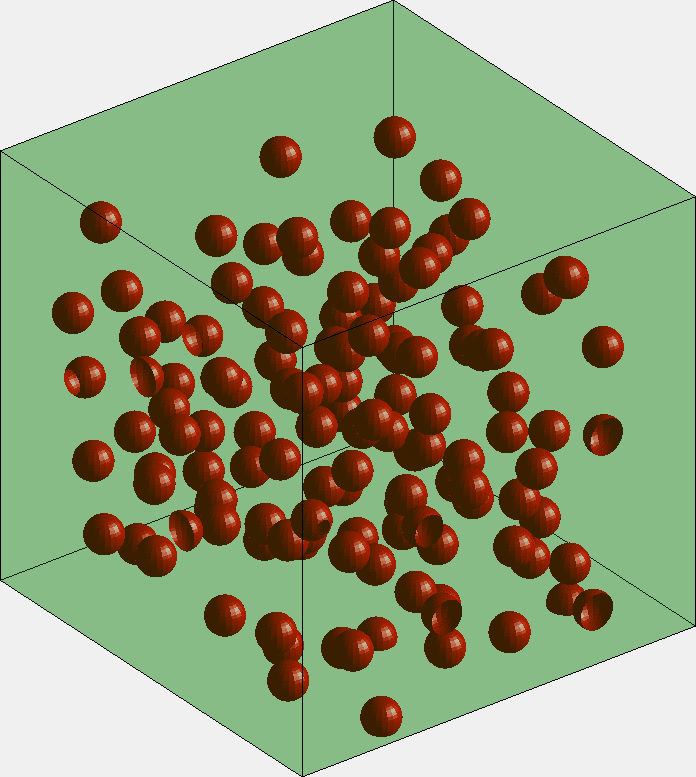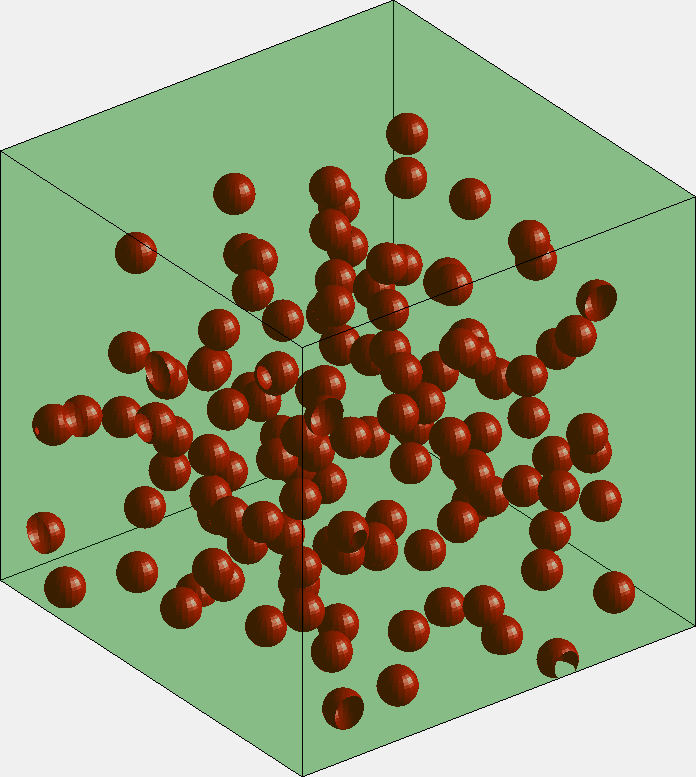

过冷水和你分享 matlab读取存储各种文件的方法 文末有独家金曲分享






