转子动力学系列(二):基于ANSYS APDL的不平衡响应分析
本文摘要(由AI生成):
本文主要介绍了刚性支承两圆盘转子的临界转速和不平衡响应。首先,文章给出了转子的问题描述,包括质量、直径、转动惯量、极转动惯量、轴段长、抗弯刚度等参数。接着,文章通过运动微分方程和频率方程求解了转子的模态频率、模态振型、临界转速及不平衡响应。最后,文章通过MASS21单元模拟圆盘,BEAM188单元模拟转轴,采用PLCAMP命令得到坎贝尔图,并通过PLVAR命令输出圆盘1和圆盘2节点的总位移变化曲线,以及通过PLORB命令得到转子系统的轴心轨迹图。
1.问题描述
如图1所示刚性支承两圆盘转子,圆盘质量m=102kg,半径R=500mm,转轴的直径d=50mm,a=400mm,设圆盘偏心e1=0.05mm,e2=0.03mm,φ1=30°,φ2=60°。求该转子涡动频率、振型、临界转速及不平衡响应。(详见《转子动力学》钟一谔 第二章刚性支承多圆盘转子的临界转速和不平衡响应,例子源于P29)
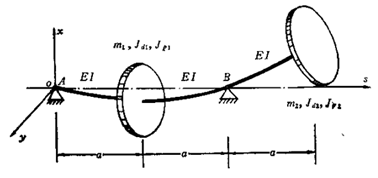
刚性支承两圆盘转子
设圆盘的质量、直径转动惯量和极转动惯量分别为mi、Jdi和Jpi(i=1,2)、各轴段长为a,抗弯刚度为EI,其运动微分方程为:
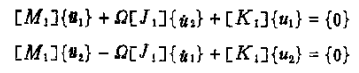 其中
其中
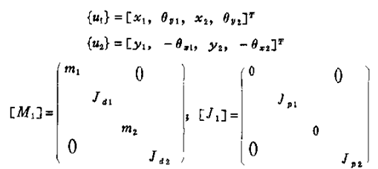 柔度矩阵是
柔度矩阵是 而
而
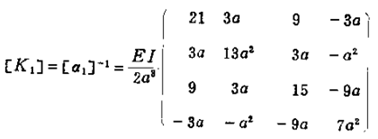
因此系统在xos平面的运动微分方程是
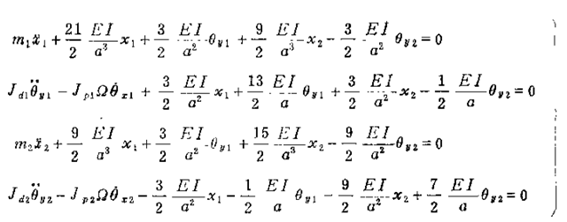
为求转子的模态频率及模态振型,只需通过在任一固定平面内的运动微分方程即可求得,令

代入上式
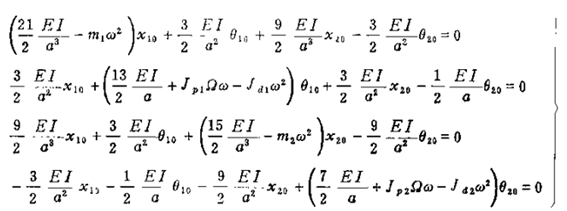
故频率方程为
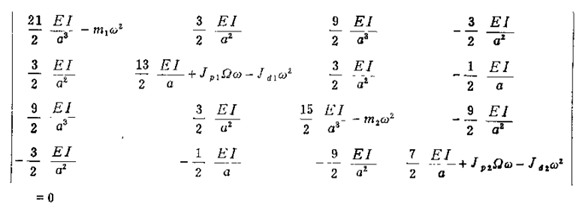
这是一个有关w的8次代数方程,对于给定的Ω,可解出4个正向涡动角速度和4个反向涡动角速度。  绘制涡动角速度随自转角速度变化曲线可得坎贝尔图,令Ω分别等于±w代入频率方程,即可分别解出在同步正涡动和同步反涡动下的临界转速。
绘制涡动角速度随自转角速度变化曲线可得坎贝尔图,令Ω分别等于±w代入频率方程,即可分别解出在同步正涡动和同步反涡动下的临界转速。

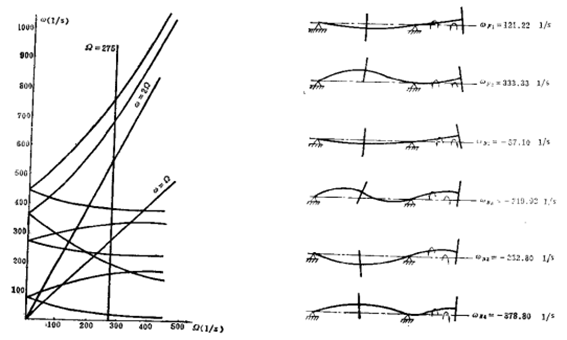
所谓转子的临界转速通常是指同步正向涡动时的临界转速。对于本算例的两圆盘转子系统,临界转速只有两个,即1158r/min和3183r/min。

在无阻力情况下,当各圆盘具有偏心的不平衡质量时,令
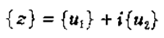
则转子的运动微分方程可写成
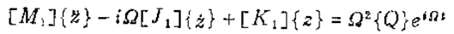
其中
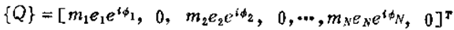
设不平衡响应的特解为
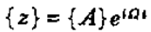
其中{A}为待定的复数列阵。把特解代入运动微分方程可得 
这是2N个线性非齐次代数方程组,对于给定的Ω,上式等号左边各项系数均为实数,可以解得 
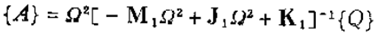
因为{Q}是2N阶复数列阵,其中有N个元素为零,故{A}中每一元素均为N个复数之和,即仍为一复数,故可表为
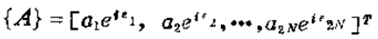
其中ai、ei(i=1,2,...N)都是已确定的值,代入特解可得

对于本例子,把数据代入特解表示的运动微分方程可得
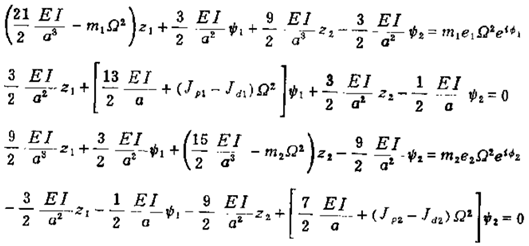
其中
 则当Ω=250 1/s时,可解得
则当Ω=250 1/s时,可解得

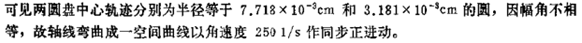 2.分析过程
2.分析过程
采用MASS21单元模拟圆盘,采用BEAM188单元模拟转轴,轴的支承处为简支约束。
后处理中采用PLCAMP命令得到坎贝尔图如下。
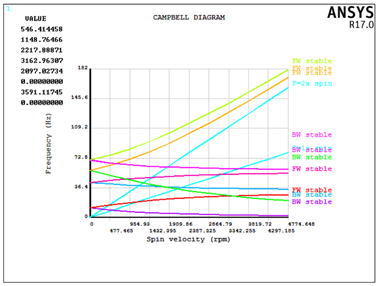
从图1可以看出,转子的临界转速按阶数由低到高分别为546.41prm、1148.76rpm、2217.89rpm、3162.96rpm、2097.02rpm、0、3591.12rpm、0,与理论解一致。
在谐响应分析中,以复数形式输入偏向质量所产生的不平衡力(X轴为旋转轴)。
对于圆盘1为

对于圆盘2为
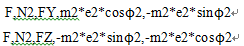
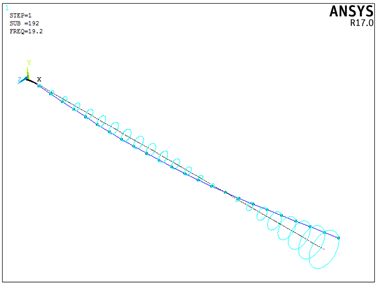
在后处理中采用PLVAR命令输出圆盘1和圆盘2节点的总位移变化曲线。

从图2可以看出,曲线在19.2Hz和52.7Hz出现峰值,该两个峰值频率对应同步正进动(涡动)临界转速1152rpm和3162rpm,与模态分析结果相对应。
当频率为19.2Hz时,采用PLORB命令得到转子系统的轴心轨迹图如下。
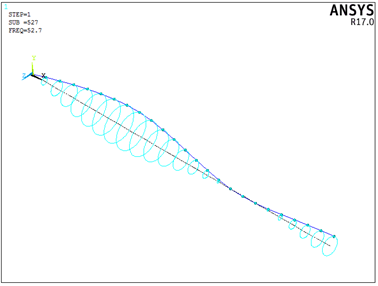
 当频率为52.7Hz时,采用PLORB命令得到转子系统的轴心轨迹图如下。
当频率为52.7Hz时,采用PLORB命令得到转子系统的轴心轨迹图如下。
当转速为250 1/s,即39.8Hz时,采用PLORB命令转子系统的轴心轨迹图如下。
采用PRORB命令输出该转速下的轴心轨迹数据,两圆盘中心轨迹为

图6中A代表椭圆的长轴、B代表椭圆的短轴,圆盘1的轴心轨迹是半径为0.797e-4m的圆,圆盘2的轴心轨迹是轨迹为半径0.308e-4m的圆,与理论解一致。
3.命令流
!建模
finish
/clear
/prep7
m=102
a=0.4
jd=6.377
jp=2*jd
ei=6.136e4
e0=2e11
r0=(4*ei/e0/acos(-1))**0.25
et,1,beam188
et,2,mass21
mp,ex,1,2e11
mp,prxy,1,0.0
sectype,1,beam,csolid
secdata,r0
r,2,m,m,m,jp,jd,jd
k,1
k,2,a
k,3,a*2
k,4,a*3
k,5,a,a
l,1,2
l,2,3
l,3,4
latt,1,,1,,,5,1
esize,0.05
lmesh,all
type,2
real,2
n1=node(a,0,0)$e,n1$n2=node(3*a,0,0)$e,n2
dk,1,uy,,,,uz,ux$dk,3,uy,,,,uz$d,all,rotx
finish
!模态分析
/solu
nmod=8 !模态数
antype,modal
modopt,qrdamp,nmod,,,on
mxpand,nmod,,,yes
coriolis,on,,,on
solnum=11 !荷载步数---不同转速的求解次数
*do,i,1,solnum
omega,(i-1)*50 !定义转速
solve
*enddo
finish
/post1
!输出全部模态计算结果
set,list !列表显示模态结果
plcamp,on,1,rpm$/noerase
plcamp,on,2,rpm$/erase
!输出CAMPBELL数据
/output,prc,txt !输出到文件,否则直接显示在输出窗口中
prcamp,on,1,rpm
/output
!获得排序后的随转速变化的涡动频率
*get,nbmo1,camp,,nbmo !CAMPBELL图模态数,同nmod参数
*get,nbst1,camp,,nbst !CAMPBELL图荷载步数,同solnum参数
*dim,campf,,nbst1,nbmo1 !同whirlf数组
*do,i,1,nbmo1 !4
*do,j,1,nbst1 !11
*get,fji,camp,i,freq,j
campf(j,i)=fji
*enddo
*enddo
!获取临界转速
*dim,crisp,,nbmo1
*do,i,1,nbmo1
*get,crisp(i),camp,i,vcri !获取最后PRCAMP命令的结果
*enddo
*stat,crisp !列表显示临界转速
finish
!谐响应分析
/solu
antype,harmic
hropt,full !完全法
synchro !不平衡激励,ratio必须为空
coriolis,on,,,on !打开科氏开关,即陀螺效应
dmprat,0 !阻尼
harfrq,0,80 !激励频率0~80Hz,即转速0~80*2*pi(rad/s)
nsubst,800 !解的结果点数,即80/800=0.1Hz为结果间隔
kbc,1 !定义阶跃荷载(与=0的渐变荷载不同,且不能用=0)
f,n1,fy,4.54e-3,-2.32e-3
f,n1,fz,-2.32e-3,-4.54e-3
f,n2,fy,1.8e-3,-2.48e-3
f,n2,fz,-2.48e-3,-1.8e-3
omega,1 !仅用于定义转速方向,其值大小无关
solve
finish
/post26
nsol,2,n1,U,Y,UY
nsol,3,n1,U,Z,UZ
realvar,4,2,,,UYR
realvar,5,3,,,UZR
prod,6,4,4,,UYR_2
prod,7,5,5,,UZR_2
add,8,6,7,,UYR_2 UZR_2
sqrt,9,8,,,AMPL_N1
nsol,2,n2,U,Y,UY
nsol,3,n2,U,Z,UZ
realvar,4,2,,,UYR
realvar,5,3,,,UZR
prod,6,4,4,,UYR_2
prod,7,5,5,,UZR_2
add,8,6,7,,UYR_2 UZR_2
sqrt,10,8,,,AMPL_N2
/gropt,logy,1
plvar,9,10 !输出圆盘1和圆盘2节点的总位移变化曲线
set,1,398
plorb !输出39.8Hz下的轴心轨迹图
prorb !输出39.8Hz下的轴心轨迹数据
finish









