Abaqus|蠕变和应力松弛的仿真模拟
1.导读
蠕变和应力松弛在生活中有不少例子。在灯柱之间,灯丝圈会随着时间不断下垂变长,这是灯丝自身重量引发的蠕变。冰川滑移也与蠕变有关。紧固件如密封圈在放置一段时间后变松了,这是因为发生了应力松弛现象。打包带变松,紧绷的橡皮筋变松等都是应力松弛现象。在一些产品设计时如压力容器,蠕变和应力松弛是需要重点考虑的因素。
2.问题描述
用Abaqus软件分别对蠕变和应力松弛进行仿真并给出其蠕变和应力松弛曲线。

图1 蠕变和仿真
3.仿真模拟
本节将建立蠕变和应力松弛的仿真模型,模拟这两种力学过程,并介绍了其主要的操作路程和分别展示了仿真结果。蠕变和应力松弛模拟过程是相似的,在ABAQUS里可分成static general和visco两个分析步完成,并且需要打开非线性功能,不然分析容易报错。
3.1 蠕变
蠕变的经典曲线如图2所示,可分为三个阶段。(1)初始蠕变阶段:应变速率随着时间增加而放慢,最后达到一个接近常数的值。(2)稳态蠕变阶段,应变速率接近常数。但是需要注意的是应力和应变率的关系随蠕变机制不同而不同。(3)加速蠕变阶段,应变率随应变增大而指数性增加。
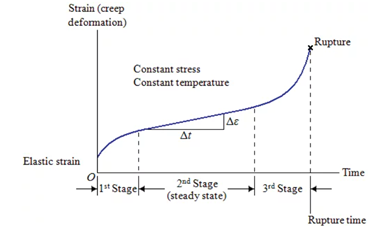
图2 经典蠕变曲线
建立如图1蠕变模型,设置如图3所示材料属性。弹性模量为200GPa,泊松比为0.3。蠕变模型选择为Plasticity-Creep,使用Time-Hardening硬化,材料参数如图所示。
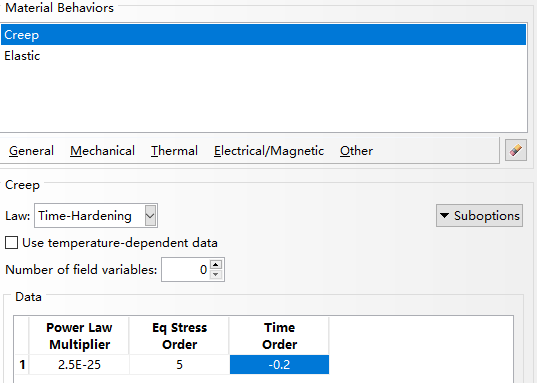
图3 材料参数设置
分析步如图4所示,注意在输出后处理场时输出蠕变应变CE。
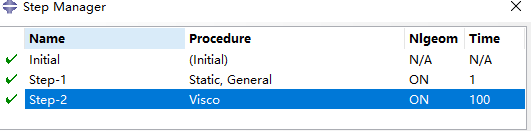
图4 分析步设置情况
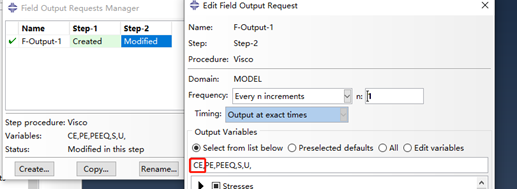
图5 输出蠕变应变CE
在Load中施加大小为3000N,方向竖直向上的集中力。为了避免应力集中,这里使用了等式约束,约束上表面一个点与上表面其他点在竖直方向相对位移为0。
图6为应变随时间变化的曲线,可知与经典蠕变曲线不一致,这是因为蠕变机制不同而导致的。图7为应力随时间变化曲线,在蠕变阶段应力恒定不变。这与蠕变的定义“在保持应力不变的条件下,应变随时间延长而增加的现象”是高度一致的。
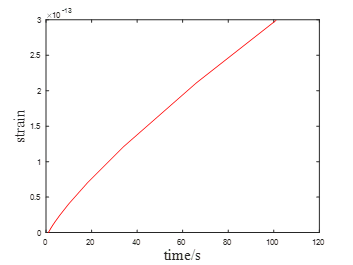
图6 应变与时间的关系
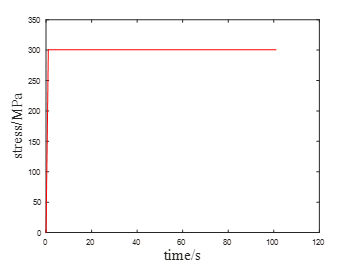
图7 应力随时间的变化
3.2 应力松弛
经典的应力松弛曲线如下图所示,应力变化主要包含两个阶段。(1)快速下降阶段,应力随着应变增大而指数型减小。(2)平缓阶段,这一阶段应力随着应变增大而缓慢减小。
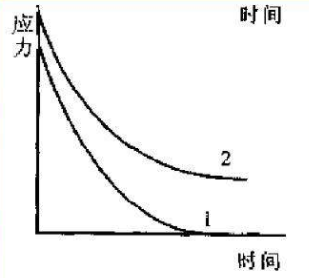
图8 经典应力松弛曲线
应力松弛和蠕变的有限元模型是一样的,操作流程也相同。应力松弛不一样的地方在于材料属性和施加的载荷不同。应力松弛使用了单轴拉伸数据和Prony粘弹性弹性本构。具体数据太多了,不好展示,可添加社长wechat获取。
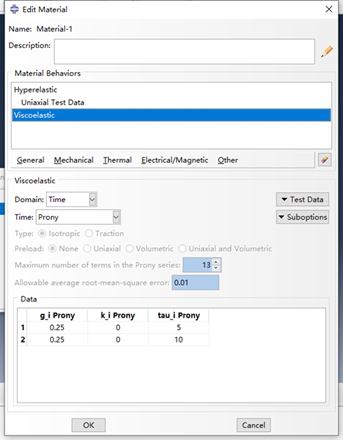
图9 应力松弛材料参数设置
松弛实验通常是施加的位移载荷,在竖直方向施加大小为100mm的位移,松弛时间为100s。
图10为松弛实验中应力随时间变化的曲线,很明显与经典松弛曲线是一致的,应力在松弛初始阶段随时间快速下降,随着松弛时间变长,应力下降趋于平缓。图11为应变随时间变化的关系,这与“应变保持不变,应力随时间延长而降低的现象”的应力松弛的定义也是较为吻合的。
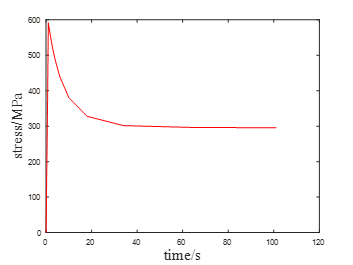
图10 松弛过程应力随时间的变化关系
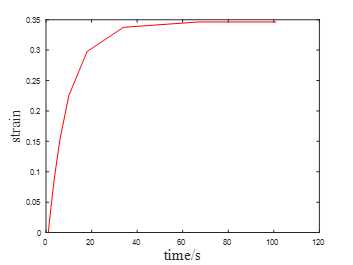
图11 松弛阶段应变随时间变化的关系
4.结论
蠕变和应力松弛是产品设计中经常需要考虑的风险因素,会对材料进行蠕变和应力松弛分析变得相当重要。本案例对蠕变和应力松弛进行了模拟,并用其定义验证了蠕变和应力松弛曲线的准确性。
源文件:蠕变和应力松弛模型CAE文件以及inp文件















