再谈海工结构疲劳分析之low cycle疲劳
1. 前言
上回讨论了S-N曲线方法和断裂力学方法的联系,提到了疲劳现象是同局部出现“塑性”紧密联系的。关于疲劳分析,在船舶与海洋工程领域,还有一个问题是比较容易混淆的,那就是所谓的low cycle和high cycle疲劳。仿真秀App公众号前不久有一篇文章《基于结构应力/应变法的焊接结构抗疲劳设计方法与应用》,提到了基于Master E-N curve(应变-循环次数)的方法,将low cycle和high cycle疲劳统一在一条曲线上分析,写得十分系统和详细,值得收藏和学习。
在这里,笔者将介绍在船舶与海洋工程领域关于low cycle疲劳分析的方法和规范(本质上和Master E-N curve异曲同工)作为我上次讨论的补充,抛砖引玉供大家思考。笔者个人认为,对low cycle疲劳的进一步认识,可以为结构工程师在评估结构局部“屈服”问题时提供新的思路(把握局部高应力的可接受程度)。本文主要参考规范:DNV Class Note 30.7,DNV-RP-C203和DNV-RP-C208。
关键字:low cycle疲劳,Neuber公式,Ramberg-Osgood关系,局部屈服
2. 船舶与海洋工程结构受到的静载荷和动载荷
在对船舶与海洋工程结构进行屈服强度设计时,无论是采用WSD方法还是LRFD方法,都需要将载荷进行分类。总体上是进行“(准)静载荷(固定载荷 可变载荷)”和“(环境)动载荷”的分类。以WSD方法为例,对结构施加静载荷和施加静 动载荷分别对应了不同的名义应力接受衡准,以DNV规范为例:
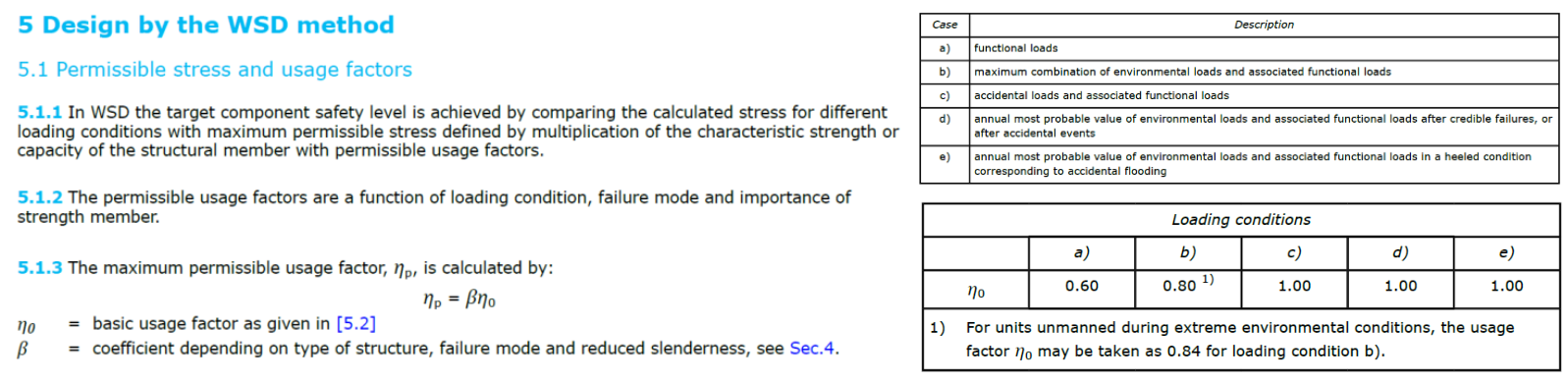
规范中a)工况对应“静载荷”工况,b)工况对应“静 动载荷”工况。名义应力接受衡准一个是0.6,一个是0.8,注意到0.8/0.6 = 1.33。事实上,这里的“静”和“动”是相对而言的:一般来说,动载荷主要关注环境载荷(波浪载荷,运动惯性载荷),总的循环次数可达10^8个;静载荷主要关注固定的或变化较慢(或变化次数较少)的设备、载货荷载,一般总的循环次数大致不超过10^3个。还有一些特殊的设备载荷,如起重机(吊)载荷,其强度和疲劳工况有自己独立的设计体系,需特殊单独分析考虑。
静、动载荷是同时存在的,一个典型的例子就是货船、FPSO等装卸货工况。货舱存在“空”和“满”的循环交替,浮体也存在有深吃水和浅吃水的差异。这时,某一个具体的受力构件的应力变化就可能是如下图这样的:
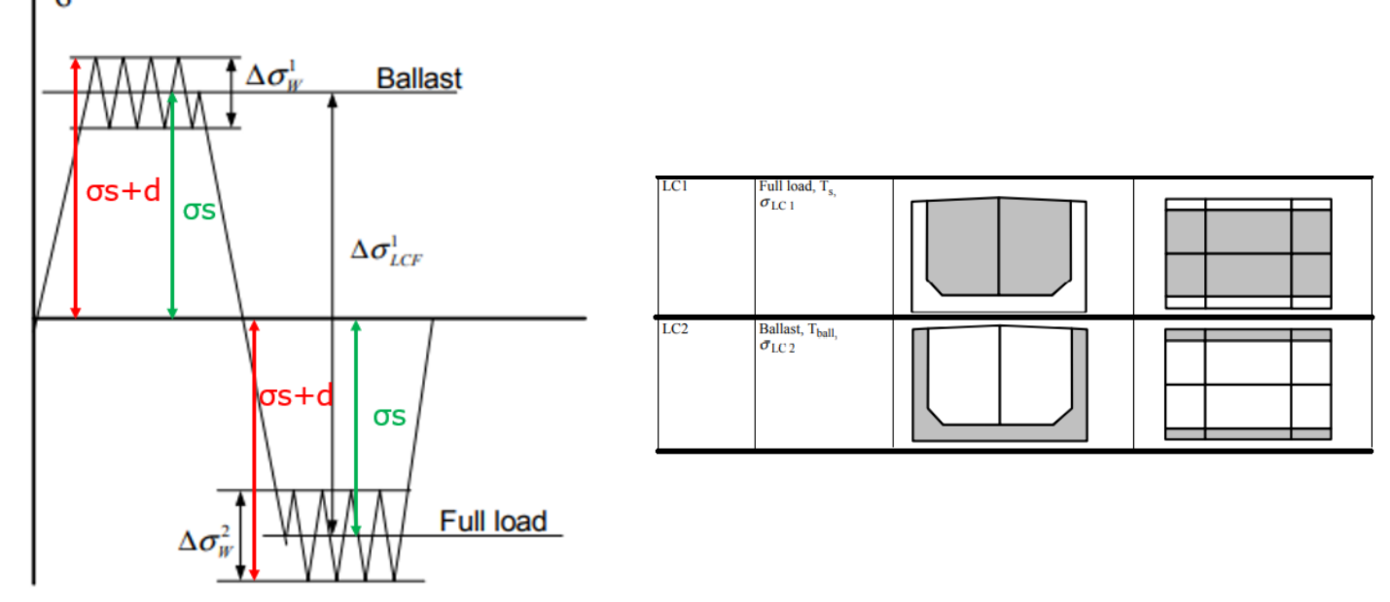
注意到:
Δσw主要是由波浪载荷引起的,其循环次数较多(~10^8),应力范围相对较小;
而ΔσLCF是由装载工况变化引起,循环次数少得多(一般低于10^3),但应力范围较大。由此可见,结构所受载荷,本身就由相对“low cycle”的(少循环)和相对“high cycle”(多循环)两部分组成。这个要与所谓“low cycle”与“high cycle”疲劳的概念相区别。
在实际工程中,有一下几点运用:
1. 对于上图中绿色标注部分的应力σs认为是“静载荷”,采用WSD-a的衡准校核;
2. 对于上图中红色标注部分的应力σs d认为是“静 动载荷”,采用WSD-b的衡准校核;
3. 对于波浪引起的应力波动Δσw,采用基于约10^8次循环的“high cycle”疲劳衡准校核;
4. 对于一些工况变化较频繁的船舶以及FPSO等,应对以ΔσLCF为应力幅值的载荷循环经行“low cycle”疲劳评估。载荷循环次数需参考operation manual等设计输入文件和规范建议,且low cycle疲劳损伤需与high cycle疲劳的结果以一定方式叠加。
对于上述第4点,在DNV和ABS的海工规范中,对FPSO和FLNG等浮式结构的low cycle疲劳分析提出了明确的要求。笔者个人认为也能成为接受局部高应力的一大依据(将在后文中讨论)。
更一般的,如果一个动过程是由两个变化速度不同的过程叠加而成的,则总的疲劳损伤可以通过分别计算这两个过程的疲劳损伤,再叠加得到(参考DNV-RP-C203)。

这个公式的主要思路如下,假设Process1(high cycle)的应力幅值为Δσ1,循环次数为n1,单独作用时的疲劳损伤为D1;Process2(low cycle)的应力幅值为Δσ2,循环次数为n2,单独作用时的疲劳损伤为D2,且n1>n2。
Process1和Process2共同作用时,考虑high cycle应力Δσ1将对low cycle过程的疲劳损伤产生贡献,表现为low cycle的应力幅值不再是Δσ2,而是Δσ1 Δσ2,循环次数仍为n2。根据应力幅值和疲劳损伤之间的简单换算关系,可得到low cycle部分的疲劳损伤变为:
![]()
而high cycle部分的循环次数减少为n1-n2,应力幅值不变,仍为Δσ1,则其疲劳损伤变为:
![]()
这样对总的损伤适当变形就可得到规范中的式子。而在规范DNV-RP-C208中也提到high cycle和low cycle的疲劳损伤可以直接相加得到总的疲劳损伤,这可能是为了简单起见,笔者个人建议需要慎重应用。
3. E-N曲线 (应变—循环 曲线)
High cycle疲劳是指发生疲劳破坏时,载荷的循环次数较多,一般认为循环次数在10^5至10^6以上(平时用的S-N曲线循环次数是从10^4起步的,规范也以为10^4边界区分high/low cycle疲劳)。参考DNV-RP-C203 Appendix F,对于10^8个总循环的波浪载荷,对疲劳贡献最大的载荷循环是10^5至10^7之间的部分,如下图;
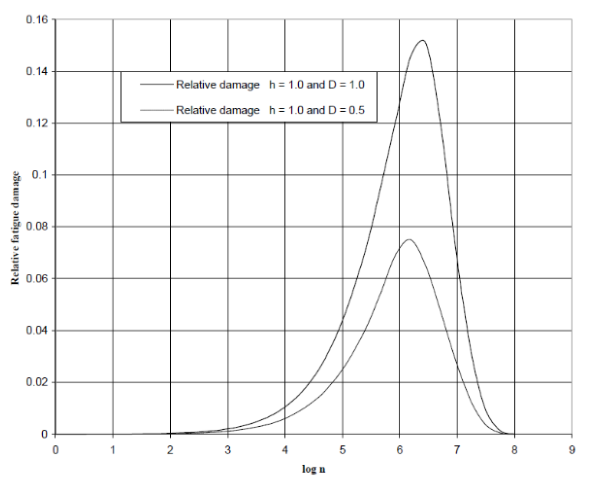
而low cycle疲劳在发生破坏时,载荷的循环次数较少,一般只有10^2至10^3次。low cycle疲劳虽然叫做“疲劳”,但因为其载荷值较大,往往可以和“屈服”问题相联系。有时候参考文献中提到的“repeat yielding”也属于low cycle疲劳的范畴。
前面提到对low cycle疲劳进行分析的要求。计算low cycle疲劳应用的是应总应变,参考规范:
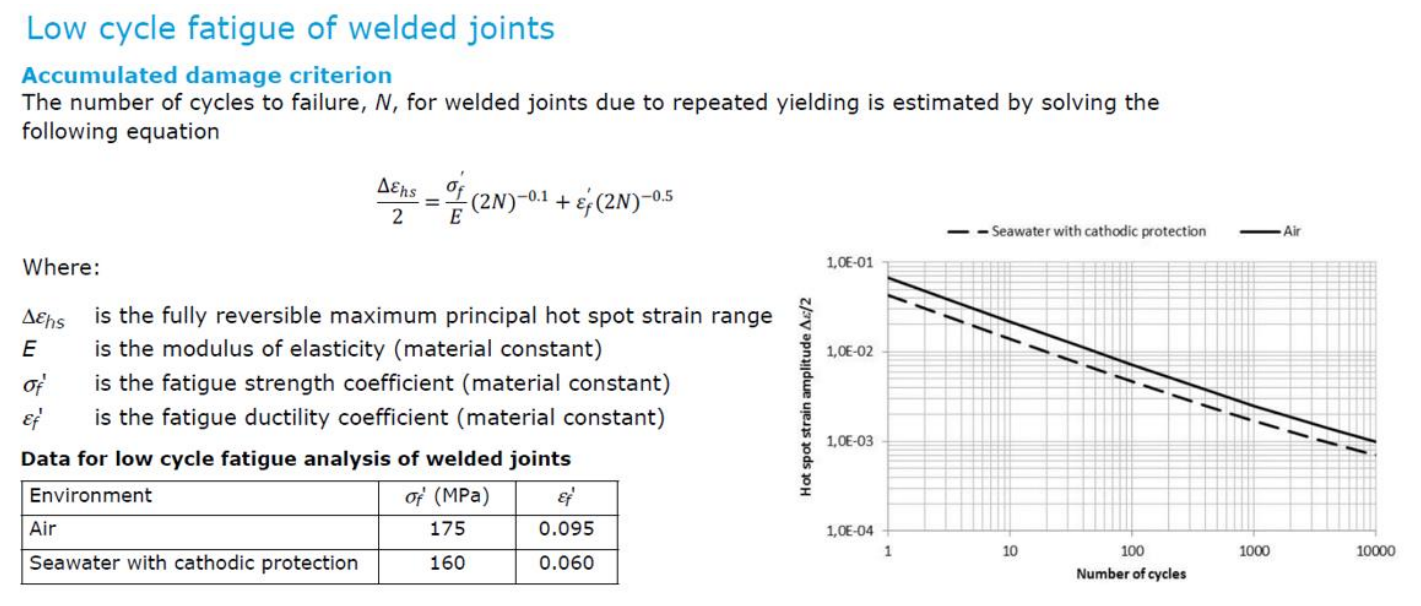
这里,将应变ε和循环次数N建立起了联系。这和我们熟知的以应力σ为参数的S-N曲线形式上也存在差异。类似的是关于“热点(hot spot)”概念的延用:热点应变εhs。
为了更好地理解这个公式,可将公式理解为elastic 和plastic两部分,并作图(以Air为例):
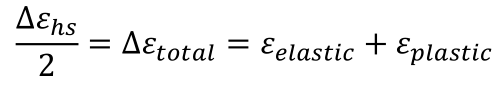
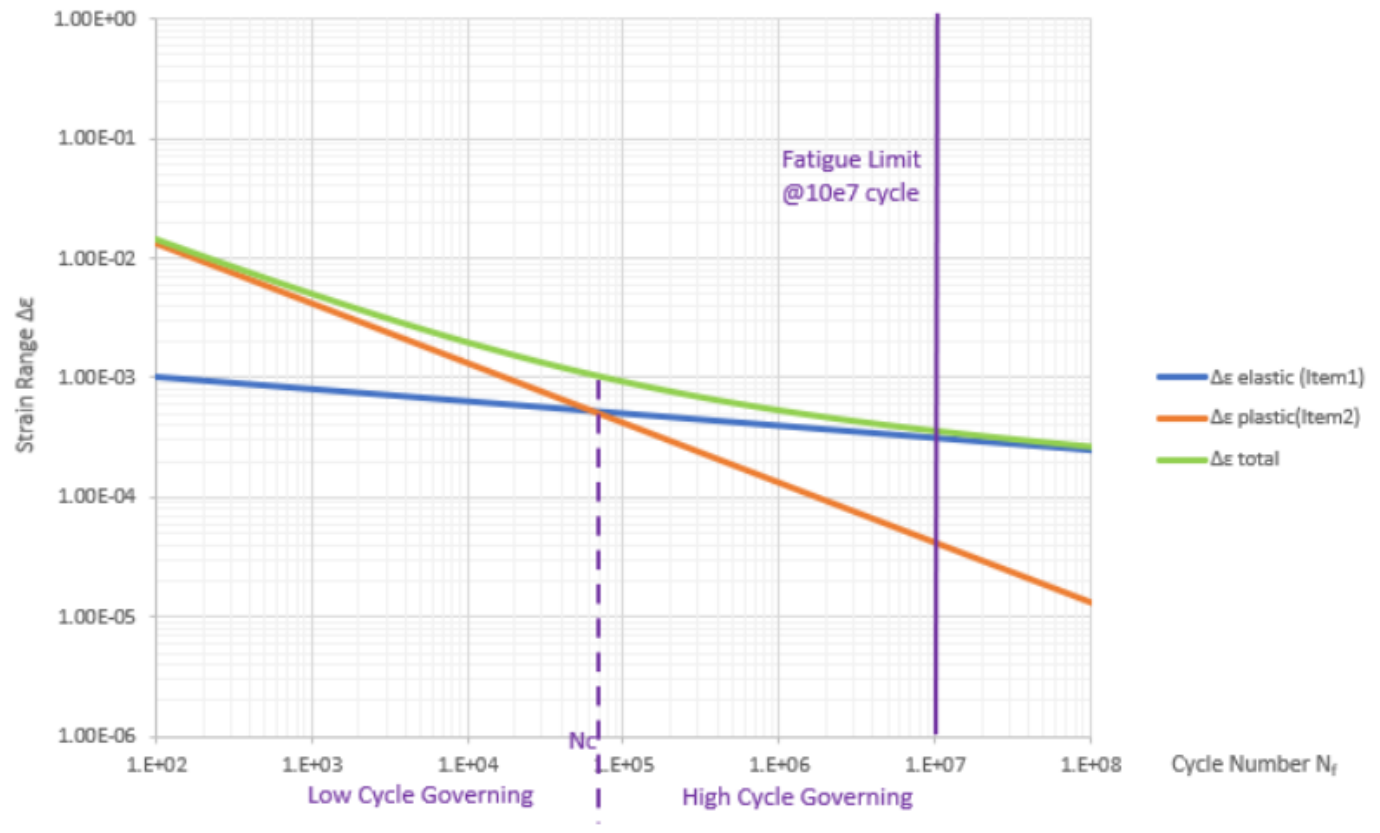
图中,可以看出在不同的循环次数下,elastic和plastic两者的贡献和比例。可以领elastic = plastic时的循环次数为Nc,Nc约为6.6x10^4。
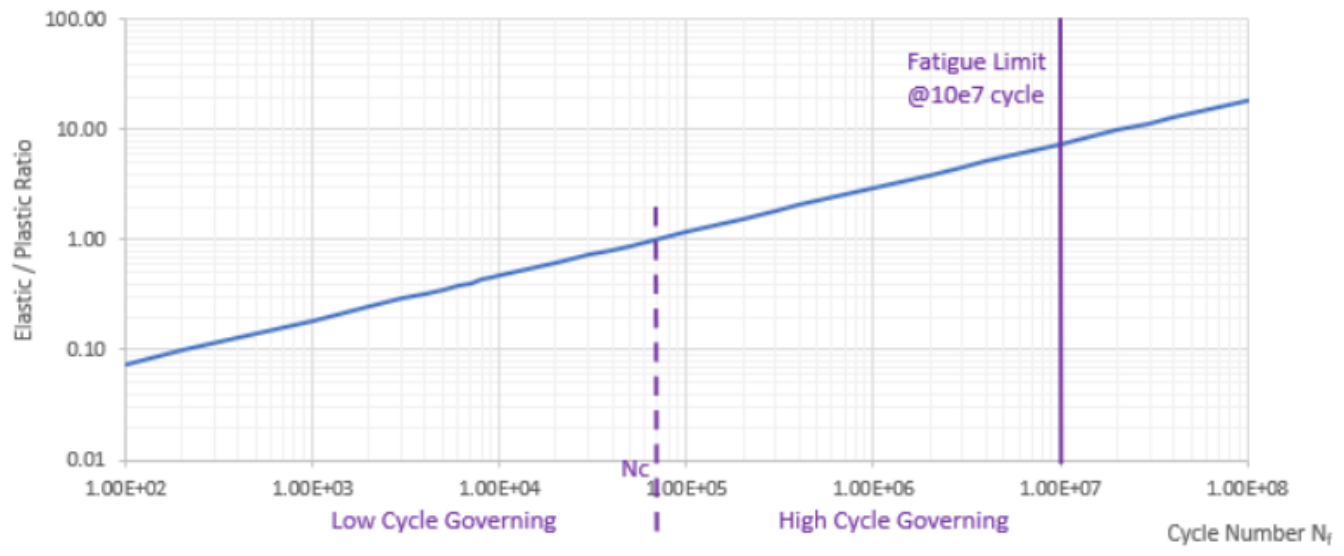
从一般的金属材料书上可以看到,对于这个公式中的循环次数N并没有很大的限制,笔者个人理解从10^2到疲劳极限10^7应该都是适用的,也就是所谓high cycle部分也是可以的。但工程上计算应力(线性)要比计算非线性的总应变要方便很多,这个公式并不常用。
接下来,我们来尝试从E-N曲线推导出S-N曲线,也许可以加深对S-N曲线的理解,这也是本文的主要目标。这个推导是笔者自己的理解和尝试,在书本和规范中都提到high cycle和low cycle的疲劳曲线是来自于试验的,但笔者认为推导过程是有利于我们思考疲劳问题的。
4. Neuber公式和low cycle疲劳S-N曲线
在笔者上一篇文章中提到了连接循环载荷下应力σ和应变ε的Ramberg-Osgood关系。

须要指出的是,这个Ramberg-Osgood关系虽然是对于金属材料的,但规范中明确了在评估焊接节点在循环载荷作用下的疲劳问题时,应该就采用这个关系(DNV-RP-C208 Sec 5.2.4.)。
有了这个式子,我们可以把应变εhs换算回应力σhs。但这个应力σhs是基于材料关系的“真”应力,而我们计算得到的应力一般是基于线弹性力学的有限元热点应力σelastic,从非线性概念的“真”应力到线性概念的有限元应力,我们须要另一个神奇的公式,那就是Neuber公式出场:
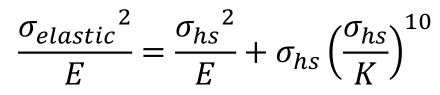
Neuber公式隐藏在DNV Class Note 30.7之中,规范也没把它的作用说清楚,过去有不少小伙伴询问这个公式的意思。这里做个思路梳理,方便理解。Neuber公式是从Ramberg-Osgood关系出发得到的。将Ramberg-Osgood关系两边同时乘以σhs,右边即得到Neuber公式的形式。左边为:σhs▪εhs,它在Ramberg-Osgood应力应变关系图上表示蓝色矩形的面积。然后定义它与有限元得到的弹性应力同其应变围成的红色矩形的面积相等,这样实现了从σhs到σelastic的对应关系,即:
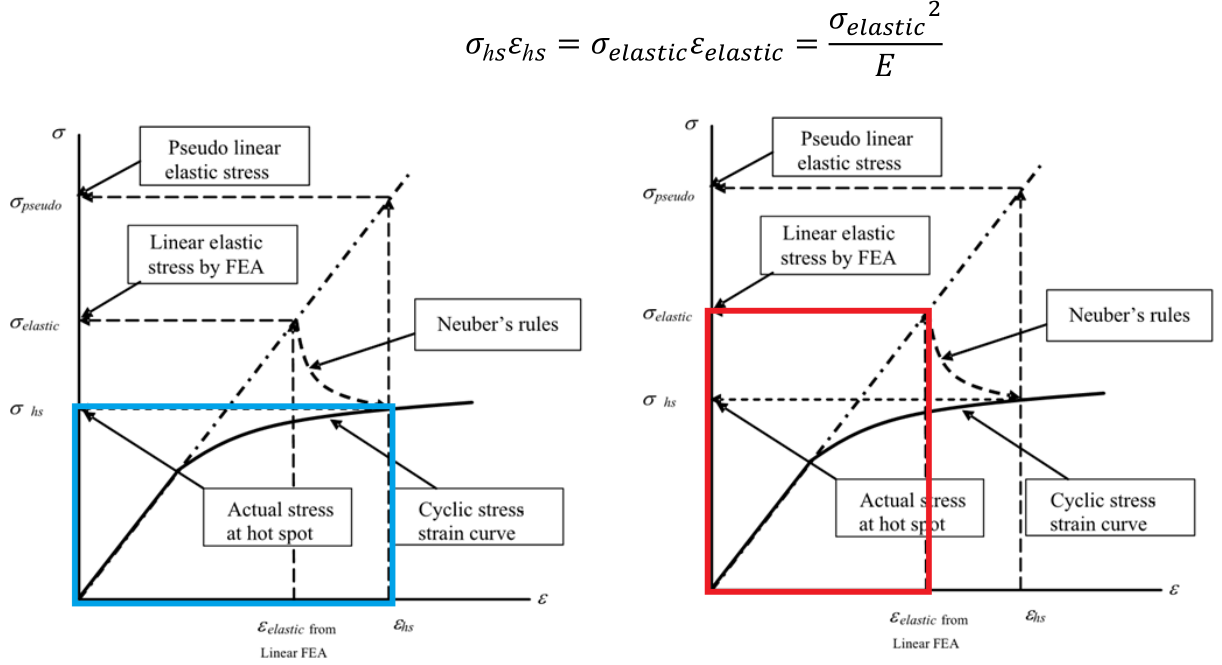
这里面积相等的条件可以理解为“变形能等价”,且由于Ramberg-Osgood应力应变关系曲线是向上凸的,这个等价关系应该是偏保守的。须要注意的是Neuber公式适用于局部高应力存在重分布可能的地方。总体来看,基于线性有限元得到的热点应力σelastic是低估应变的,通过Neuber公式可以得到对应“正确应变”εhs的应力σpseudo,这个应力将用来生成S-N曲线。
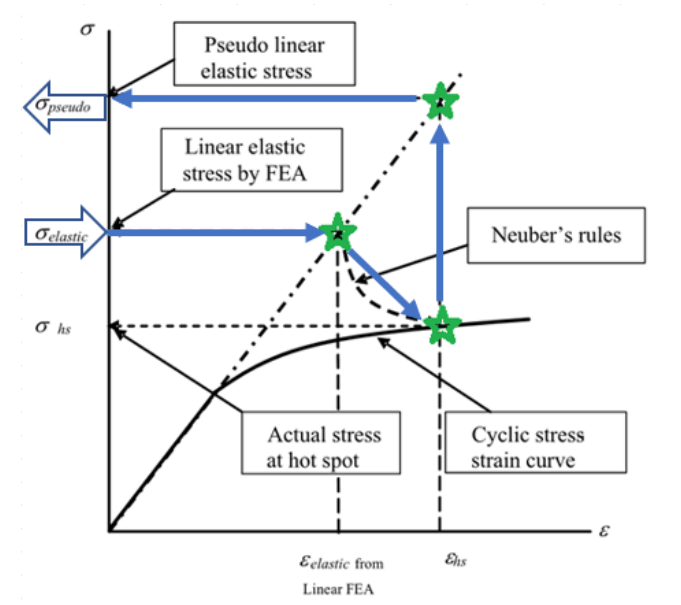
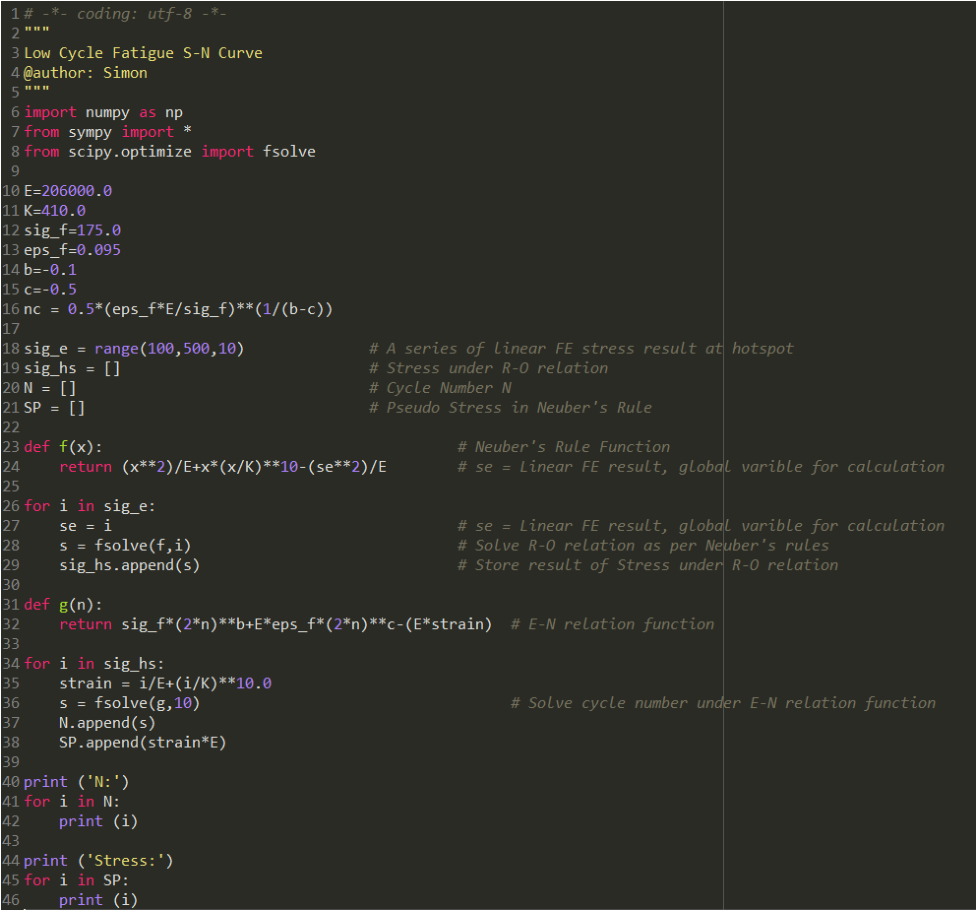
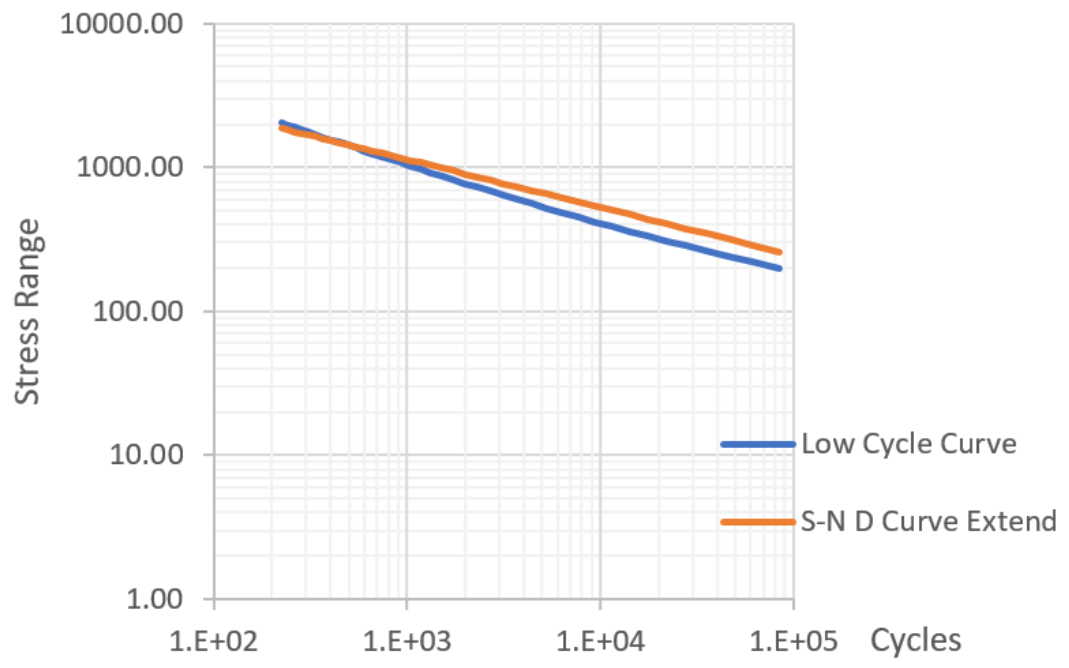
这样,我们可以定义一系列σelastic,通过上述过程得到εhs,并计算对应的循环次数N,再得到σpseudo,将σpseudo和N绘制成S-N曲线。这个过程需要求解非线性方程,可通过编写程序来实现。本文附Python小程序供大家参考。
从绘制的曲线来看,在对数坐标系下Low Cycle Curve的“线性”特性是比较明显的(斜率在2.5~3.0之间),符合一般S-N曲线的规律。将其与S-N曲线中的D曲线的延长线相比,是比较接近的。在工程上,DNV Class Note 30.7即将D曲线的延长线作为low cycle fatigue评估的曲线。当然规范里中对σpseudo,进行了进一步的修正,详见规范的具体章节内容。
5. 几点思考
了解Neuber公式,对结构评估是好处多多的。在工程上经常遇到这样的情况:某个结构的high cycle (波频)疲劳FLS算够了,但局部ULS应力比较高,线性有限元计算得到的应力高于屈服应力(如1.25倍的屈服应力,甚至更高)。一个典型的例子就是半潜平台Pontoon和Column连接处的大肘板。进一步分析可知,大肘板上的应力主要来自于:
1- 平台在波浪中的变形(用于波频疲劳计算),如下图:
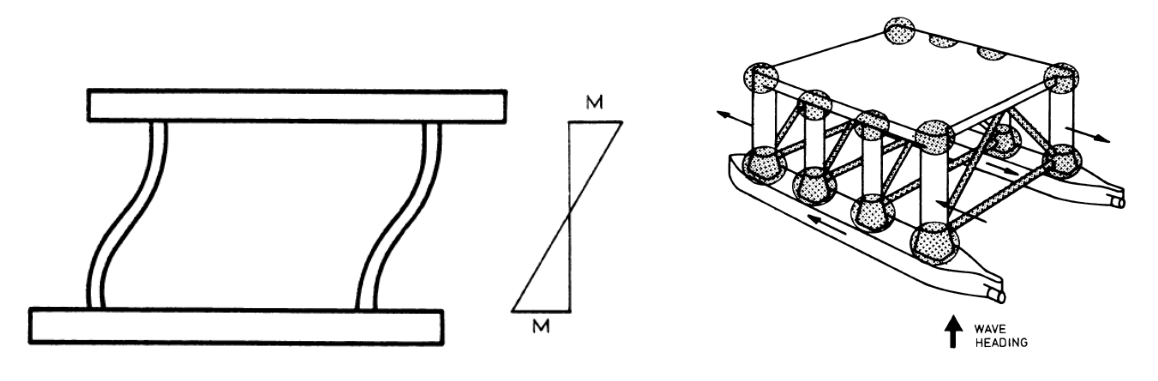
2-平台的(静)装载工况如下图
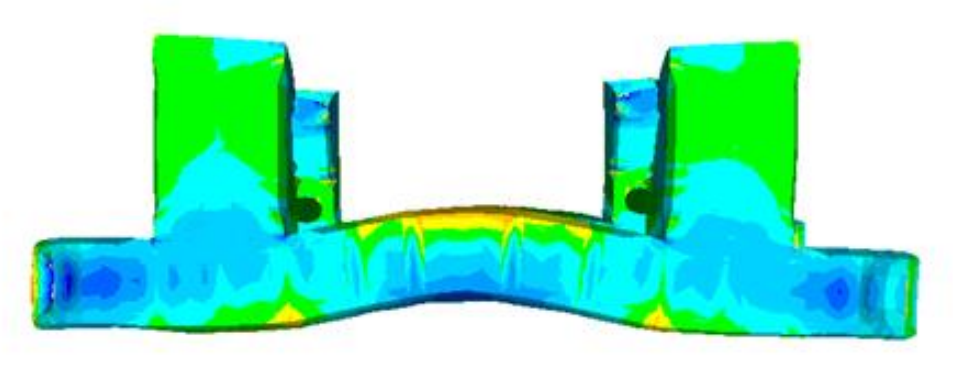
这两部分应力叠加(可能包含不同的载荷系数),形成了局部的总的高应力。这时,可以通过进一步分析装载工况的循环次数和应力水平来评估这样的高应力是否可以接受,而不是一味的增强增大板厚(类似这种变形为主要因素的情况无法通过局部增强得到满意的结果)。
此外,Neuber公式还可以帮助快速评估真实应变的水平,避免过大(拉)应变导致的断裂,尤其是对于焊接节点。对于非线性有限元分析,可以快速地进行线性分析得到弹性应力水平,再进行非线性分析,参考Neuber公式来从另一角度判断结果的合理性。
Python Low Cycle Fatigue小程序