浅谈海洋工程结构物疲劳分析中的S-N曲线方法和断裂力学方法
1. 引言
应用S-N曲线方法分析海洋工程结构物的疲劳问题是目前最为常规的计算手段和设计依据。然而工程实践表明,疲劳破坏案例占到所有结构破坏案例的大多数,远多于屈服和屈曲,这从侧面表明S-N曲线方法可能存在一定缺陷。尽管如此,S-N曲线方法因其直观且易于工程应用的特点,相信今后一段时期内仍然是海洋工程结构物主流的计算分析方法。
我们也可看到近年来,断裂力学方法不断发展。笔者对断裂力学方法在工程上的应用十分关注,目前的主要应用有:
- 在规范层面,目前船舶行业已经对LNG Type B货舱要求做裂纹扩展分析;
- 在海工结构(导管架平台)工程应用层面,工程临界分析(ECA)也经常得以应用来分析“已知”裂纹,以支持维修决策和制定检验方案等等;
- DNV-ST-0119中,对于浮式风机基础,视断裂力学方法为疲劳寿命计算的方法之一。
目前对于疲劳分析方法,应用S-N曲线和断裂力学方法进行分析,无论从书本、规范还是应用都似乎分得很开,有“不相往来”的感觉。
笔者认为研究学习,理解好两者存在的关联,认识断裂力学分析的一些思路和方法对更好得应用S-N曲线方法、一定程度克服其不足很有帮助。本文从工程的角度总结了一些心得体会,抛砖引玉,仅供大家参考。
2. 路线
本文的思路是从大家熟悉的S-N曲线方法入手,讨论应力范围Δσ的意义并引入应力强度因子,建立其与断裂力学方法的联系。再通过一个例子,互验断裂力学方法和S-N曲线方法的结果(附Python代码参考)。主要参考规范DNV-RP-C203以及BS7910。理清一些概念:
- 应力集中系数SCF和应力强度因子K
- ECA和FAD
- 两种计算方法的联系
对断裂力学,笔者自认为还有很多东西没有掌握,文中难免有误,欢迎大家指正。
3. S-N曲线方法中的应力和循环载荷下的应力应变曲线
在采用S-N曲线方法考虑下方左图的普通对接焊细节,一般认为它属于D Curve至F Curve的细节,对应Fatigue Limit (107个常应力循环)的应力范围约为40~50 MPa,即应力幅值仅为20至25MPa。给人的直观印象是这个应力水平很低,结构完全处于弹性状态。
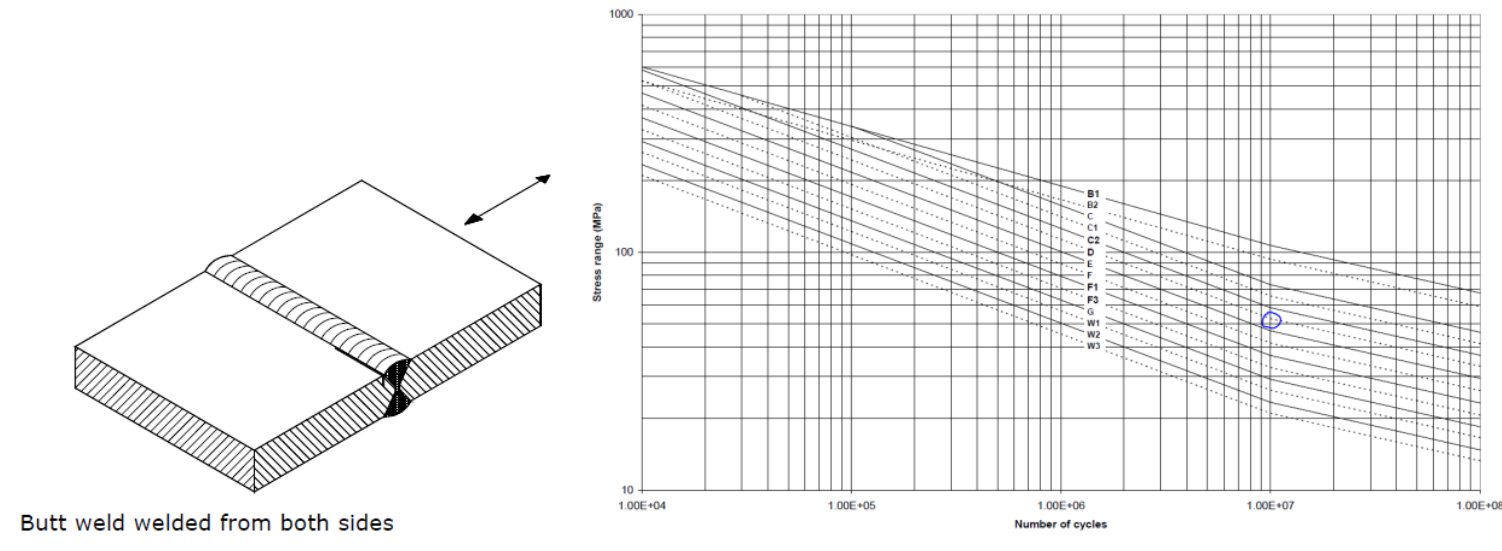
需要注意的是S-N曲线中的应力范围Δσ并非“真实”的应力而是“名义”上的应力(或者叫工程应力)。即使采用我们常用的“热点应力”(t x t有限元网格下的应力插值),它也不是真实的应力,而是一种和D曲线“配合”使用的“计算”应力。这可以从相对最接近真实应力的缺口应力(notch stress)来理解。
规范中(DNV-RP-C203)对缺口应力的表达由下图所示。采用非常细密的网格来表达焊接材料和母材的连接区域(半径为1mm的弧线),这样得到的应力需要结合缺口应力S-N曲线(Notch Stress S-N Curve)来计算疲劳损伤。可以想象要表达半径为1mm的弧线,对单元数量和形状的要求巨大。但其相对比较准确地表达了焊接材料的“几何形状”的影响,故可认为其接近真实的应力水平。下图中,红笔给出了规范提出的在名义载荷为1时,各缺口应力的值。可知道缺口应力和热点应力之间存在2.5倍的关系(即焊接材料的几何影响)。笔者给出简单的FE分析,得到的结果和规范很相近。
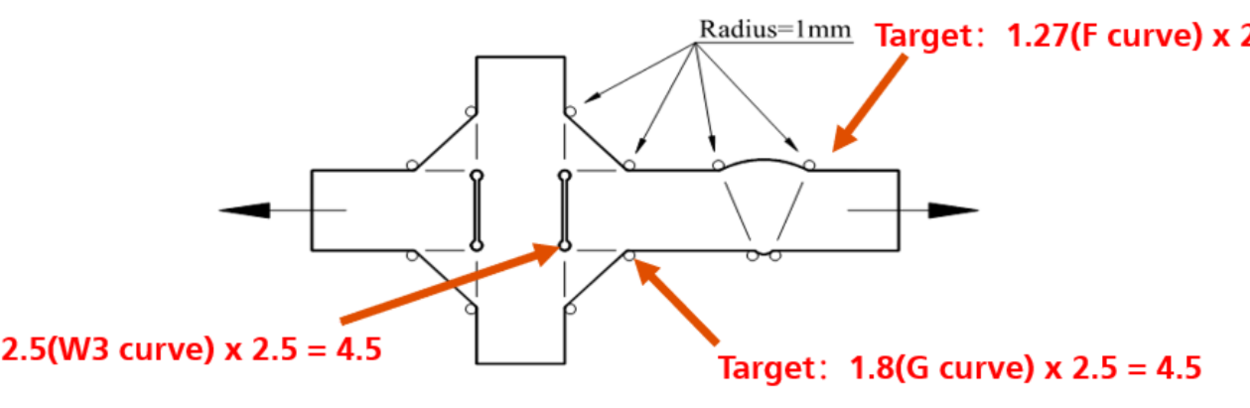
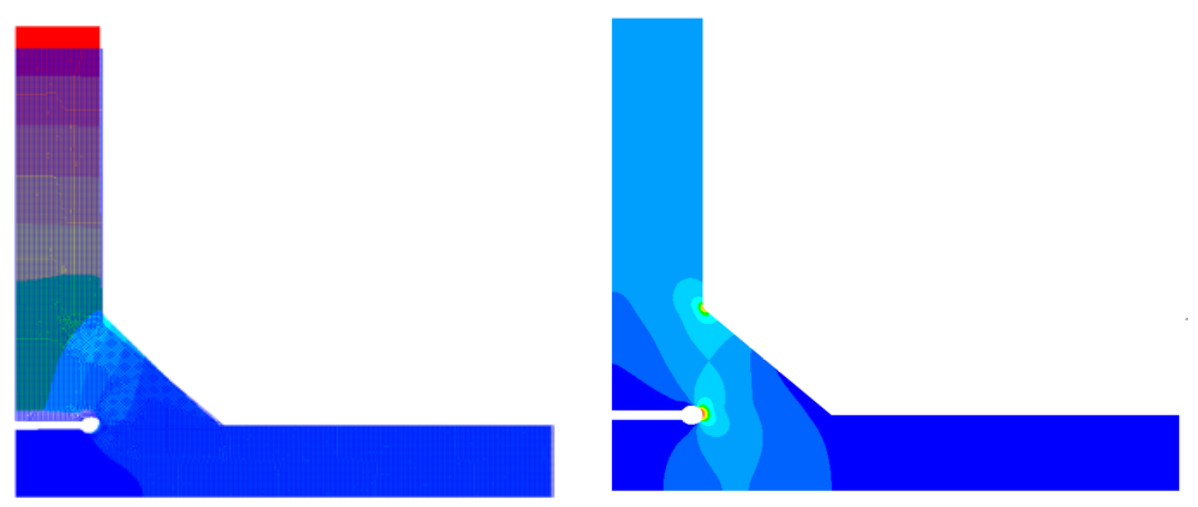
这样来看,对于前面的对接焊细节,107循环下疲劳极限的名义应力单幅值为25MPa,对应的缺口应力单幅值可以达到25x1.27x2.5=80MPa。(若不采用设计S-N曲线而采用“平均”S-N曲线,名义应力单幅值为35MPa,对应的缺口应力单幅值可以达到35x1.27x2.5=110MPa)
这个100MPa左右的应力似乎仍然在弹性范围内,但是材料在循环载荷作用下的应力应变曲线和材料本身的拉伸曲线(或者理想弹塑性曲线)是有较大差异的。以32钢为例,如下图所示:
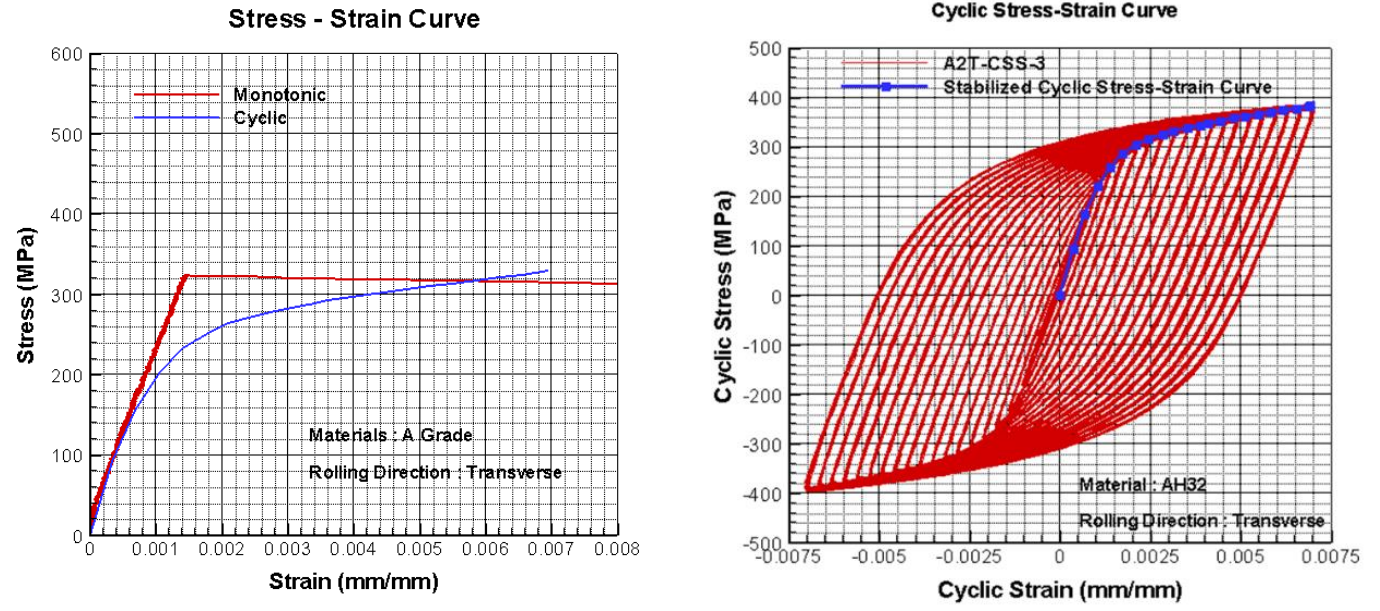
从左图可以看出,在循环载荷作用下,材料的弹性段会大大缩短,“屈服点”会提前,或者说没有明显的屈服点,材料在应力还比较低的时候就表现出“塑性”。右图显示了循环载荷下的应力应变曲线可以由试验通过几次加载达到“稳定”状态时确定,且一个试件理论上可以做多组数据点。通过观察循环载荷下的应力应变曲线可以看出大致在100MPa附近,材料即开始明显表现出塑性,参考应力应变的公式如下(K为材料系数,约410~600MPa):
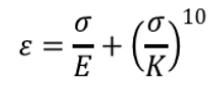
还记得上一节中我们得到的80~110MPa吗?和这里的100MPa十分吻合,但这不是什么巧合,恰恰反应了一个我们容易忽视和误解的问题,即疲劳问题,其实质是和局部出现屈服(塑性)密不可分的,虽然从名义应力来看,应力水平还远低于强度意义上的屈服应力。
理解了这一点,我们就更容易接受和理解断裂力学的方法和思路了。下面是一些概念的整理:
a) 应力集中系数SCF
SCF是在弹性假设下,应力水平在“局部”由于“几何形状”因素相对宏观(远场)的应力升高现象。
σ local = SCF ▪ σ remote
前面已经提到,用SCF得到的局部应力是一种配合S-N曲线计算疲劳损伤的“计算”应力。并不能反应“真实”的应力情况(尤其是有裂纹发展的情况)。但S-N曲线方法有大量的实验基础,结合线性疲劳损伤叠加假设易于理解,工程上实现较为容易、高效,仍然是普遍适用的方法。
b) 应力强度因子K
既然SCF不能反应裂纹尖端的“状态”,于是科学家们换了个思路,引入了应力强度因子K的概念,以最典型的I型张开裂纹为例,公式为:
![]()
式子中σ remote为远场应力,Y(a)为几何系数,a为裂纹长度。从微观的角度,裂纹的发展是裂纹端部的金属“化学键断开”,能量释放的过程。K的单位是N/mm3/2,是σ remote,构件几何特征,裂纹长度a的函数。
有了K的定义,对于应力循环Δσ就有ΔK:
![]()
帕里斯定律(Paris law)把每次应力循环下裂纹的增长da/dN和ΔK联系起来:
![]()
式中C、m、ΔKth 和Kmat都是和材料相关的系数,其中:
ΔKth是一个门槛值,只有当ΔK大于它时,裂纹才会扩展;
Kmat是材料的断裂韧度,当K的值达到它时,材料的裂纹将不稳定地快速增长。Kmat可由CTOD试验或者J积分获得。
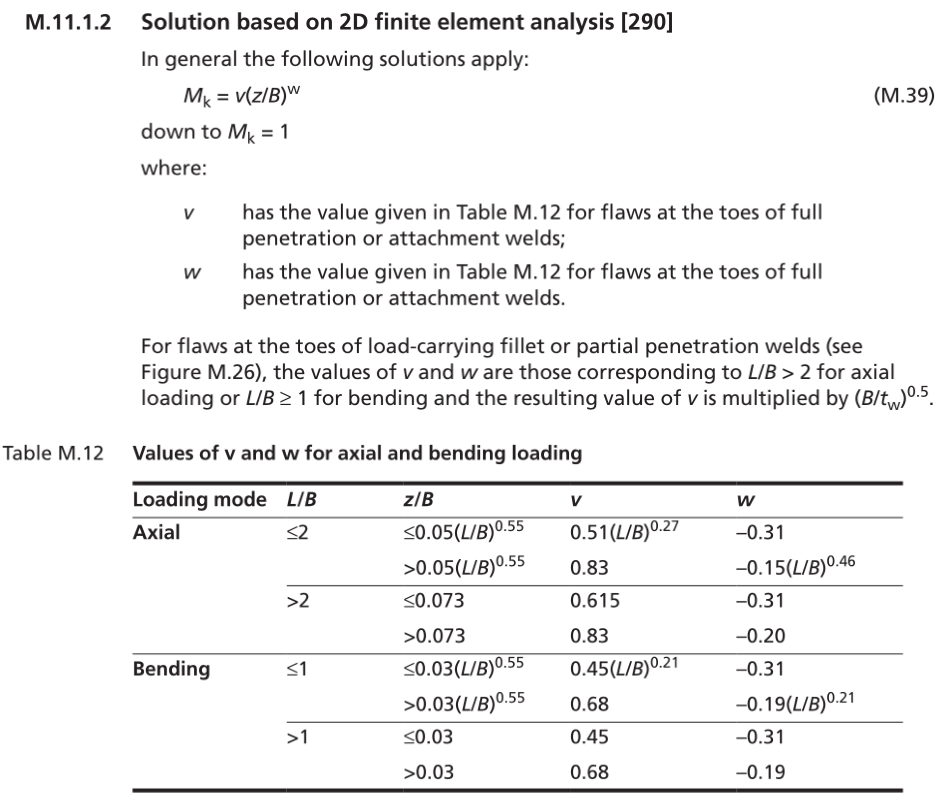
规范BS7910,Annex M中给出了典型构件形式K的计算公式,通用的公式和主要意义如下(公式比较繁琐,系数也一大堆,推荐一款软件crackwise来做工程计算)。对于特殊复杂构件,K可用奇异单元通过位移外推法进行数值求解。

c) ECA和FAD
ECA (Engineering Critical Assessment) ,即工程临界评定,是对有焊接缺陷的结构进行断裂和疲劳失效评定的一种分析。快速入门可查看中国船级社CCS出的《工程临界评定技术服务指南》。这里做一下简单的介绍。
简单来说,ECA做2件事情,第一是判断构件的强度(韧性)安全性(还记得前面提到的Kmat吗?),主要方法是用FAD失效评定图;第二是估计裂纹的扩展。
FAD (Failure Assessment Diagram),即失效评定图,是通过判别评定点与失效曲线的位置评价结构安全性(是否会发生不稳定的断裂)。FAD图如下:
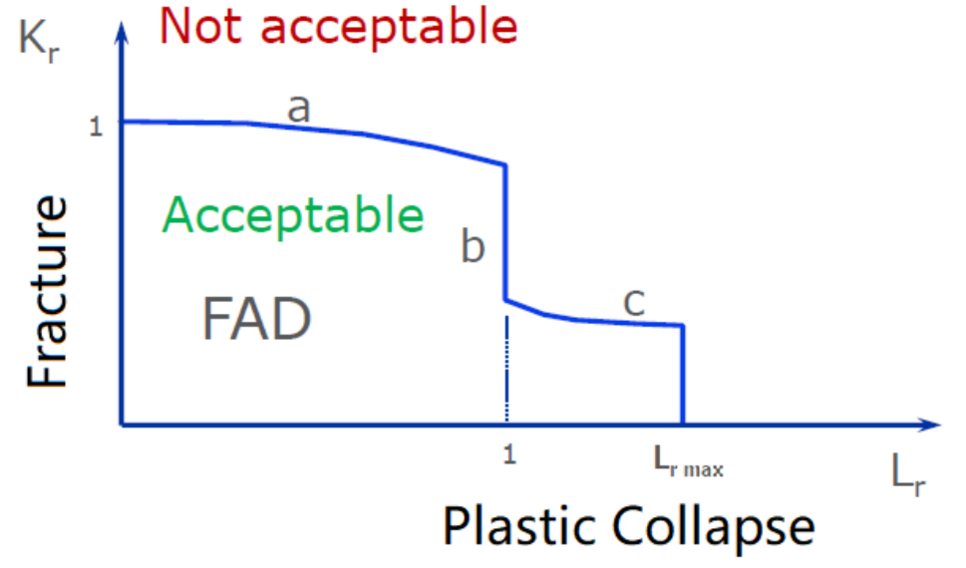
通过判断构件的状态是否在可接受区来评估。其中纵轴是断裂比Kr,横坐标是载荷比Lr。
简单起见,可以这么理解:Kr = K/Kmat, Lr = σ/σ yield (Lrmax = σtensile/σ yield)
d) 两种计算方法的联系
这里先说数学上的联系。把![]() 代入式子
代入式子![]() ,稍做变形。
,稍做变形。
在一定的Δσ循环下:
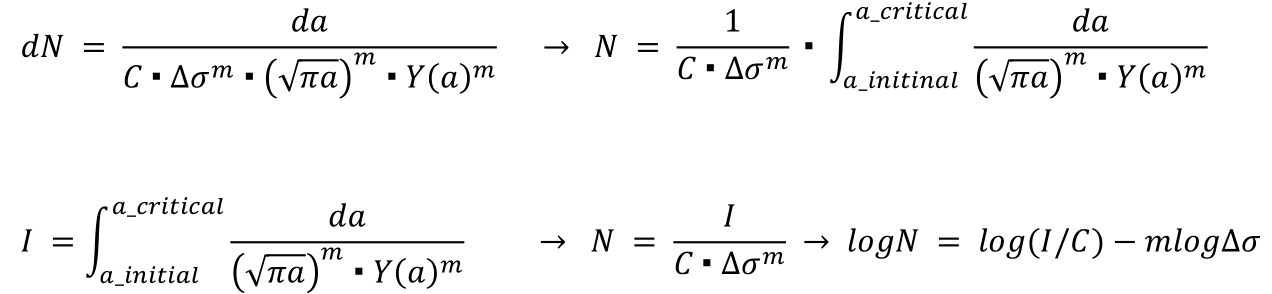
看到最后的![]() ,是不是很眼熟呢,对了它就是S-N曲线的表达式。所以从数学表达上来说,S-N曲线可以理解为是断裂力学的“积分形式”,从某种意义上是等效的!
,是不是很眼熟呢,对了它就是S-N曲线的表达式。所以从数学表达上来说,S-N曲线可以理解为是断裂力学的“积分形式”,从某种意义上是等效的!
需要注意到I是一个对裂纹长度的定积分,它的积分下上限为a_initial和a_critical,其中:
a_initial是初始裂纹长度,计算表明积分结果对它的取值十分敏感。a_critical是裂纹发生不稳定扩展时的长度,计算表明积分结果对它的取值敏感程度不高。
4. S-N曲线和裂纹扩展曲线
S-N曲线以应力范围Δσ和循环次数N为变量,一个Δσi对应一个Ni。而裂纹扩展曲线以ΔK和单位应力循环下裂纹长度的变化率da/dN为变量,反应了裂纹扩展的过程,它比S-N曲线多一个变量,即裂纹长度a。可以这么理解裂纹扩展曲线,即它是S-N曲线上每一个点的展开(或“微分”,S-N曲线是积分的结果)。
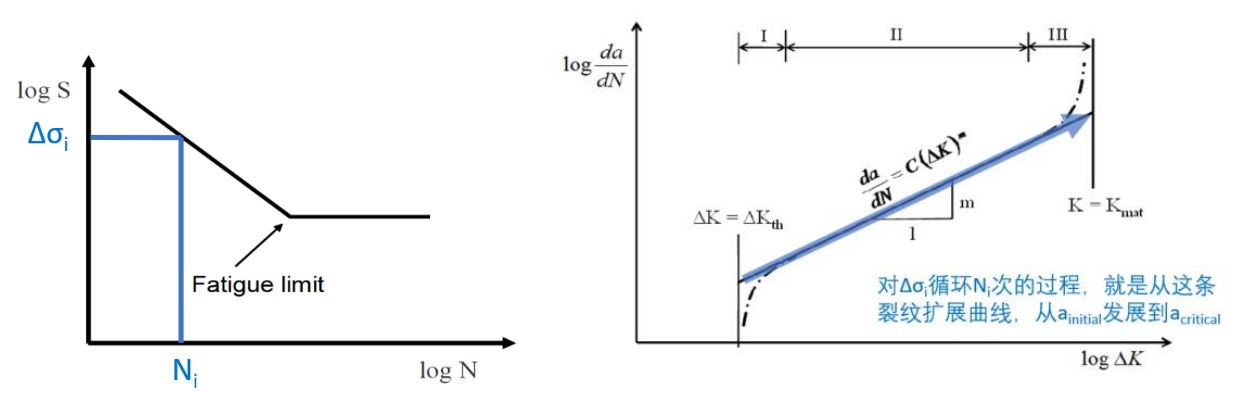
两个曲线的特征还有如下对应关系:
- S-N曲线存在Fatigue limit点,即当Δσ很小时,构件不出现疲劳破坏。 这从 ΔKth的角度很好理解,因为只有当ΔKth < ΔK时,裂纹才会扩展。而ΔK正比于Δσ。
- S-N曲线和裂纹扩展曲线具有相同的斜率,只是差一个正负符号。
- 裂纹扩展曲线所分成的I区(裂纹萌生)、II区(裂纹扩展)、III区(裂纹破坏)可以评估得到相对更真实的疲劳损伤情况,比S-N曲线的疲劳损伤线性叠加的概念更合理科学。但同时,采用裂纹扩展曲线需要更深入地考虑载荷循环的先后顺序等因素,工作量有相当的增加。
- 同S-N曲线一样,近年来裂纹扩展曲线的获得也进行了大量试验。在实际应用中“设计S-N曲线”是将“平均S-N曲线”向“下”移动两个标准差来获得97.7%的“存活概率”(考虑试验数据呈正态分布)。类似的,“设计裂纹扩展曲线”也是将“平均曲线”向“上”平移两个标准差来得到。BS9710推荐的针对焊接节点的单斜率设计裂纹扩展曲线为m=3, C = 5.21x10-13。
5. 一个来自于规范的例子
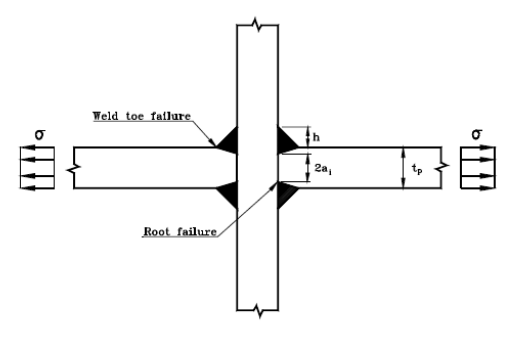
DNV-RP-C203, Sec 2.8有一个对于深熔焊的尺寸有一个推荐(如下图),用来判断深熔焊根部和焊接趾端两者谁更容易发生疲劳破坏。由于深熔焊根部的裂纹无法被检查到,所以设计上要避免它会先于焊接趾端发生疲劳问题。
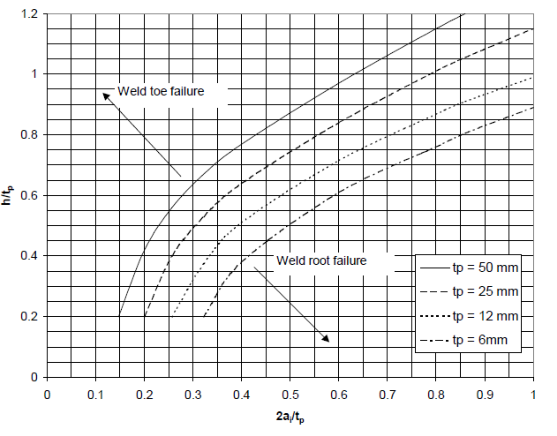
我们以tp=25mm为例,在设计图谱上首先选取若干设计点(如下图绿圈所示)。然后参考BS9710,计算根部裂纹扩展的总循环次数N。
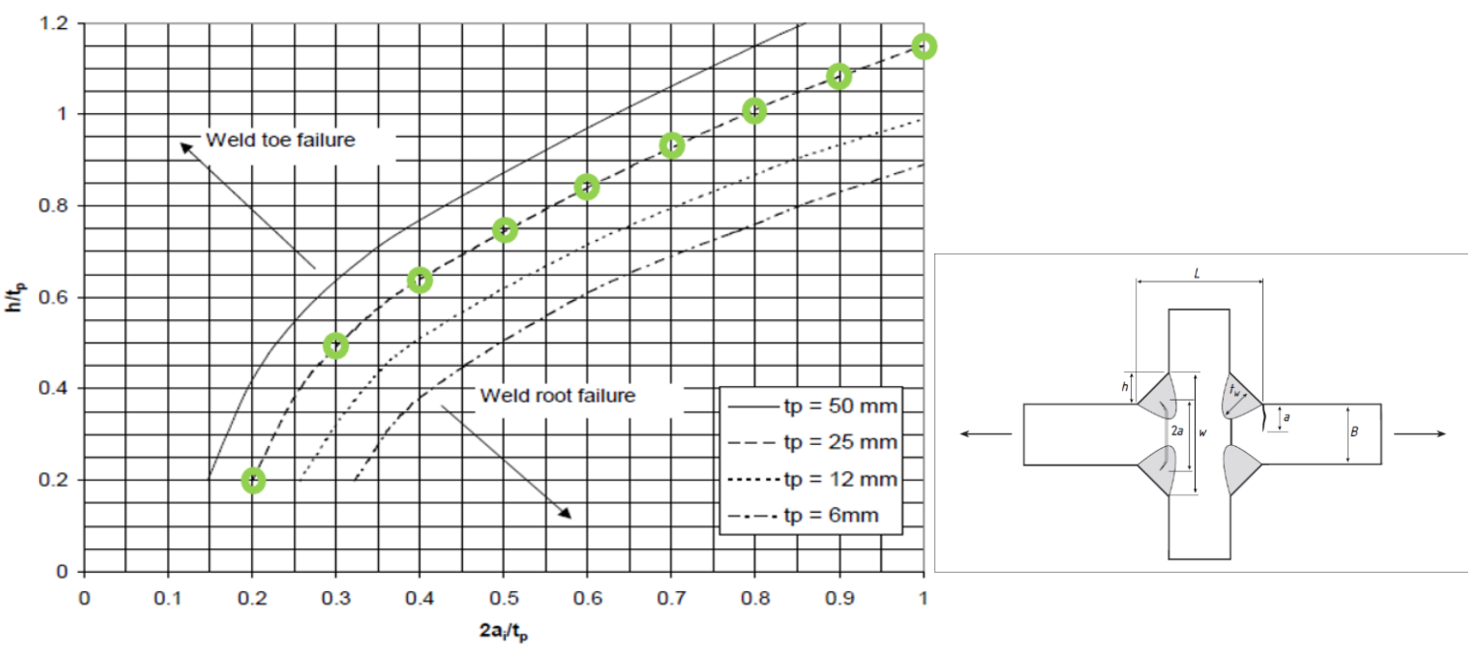
这里需要注意,积分的上下限的设定。根部的裂纹扩展可以认为是从原来的间隙2*ai到0.7*W。参考应力范围Δσ根据DNV-RP-C203,焊接趾端的满足G curve,可简单选取略大于G curve对应107循环的应力范围30MPa (选取的应力不低于Fatigue Limit即可),计算根部的总循环次数是否能大于107。笔者编写了Python小程序来记录循环次数之比,供参考。
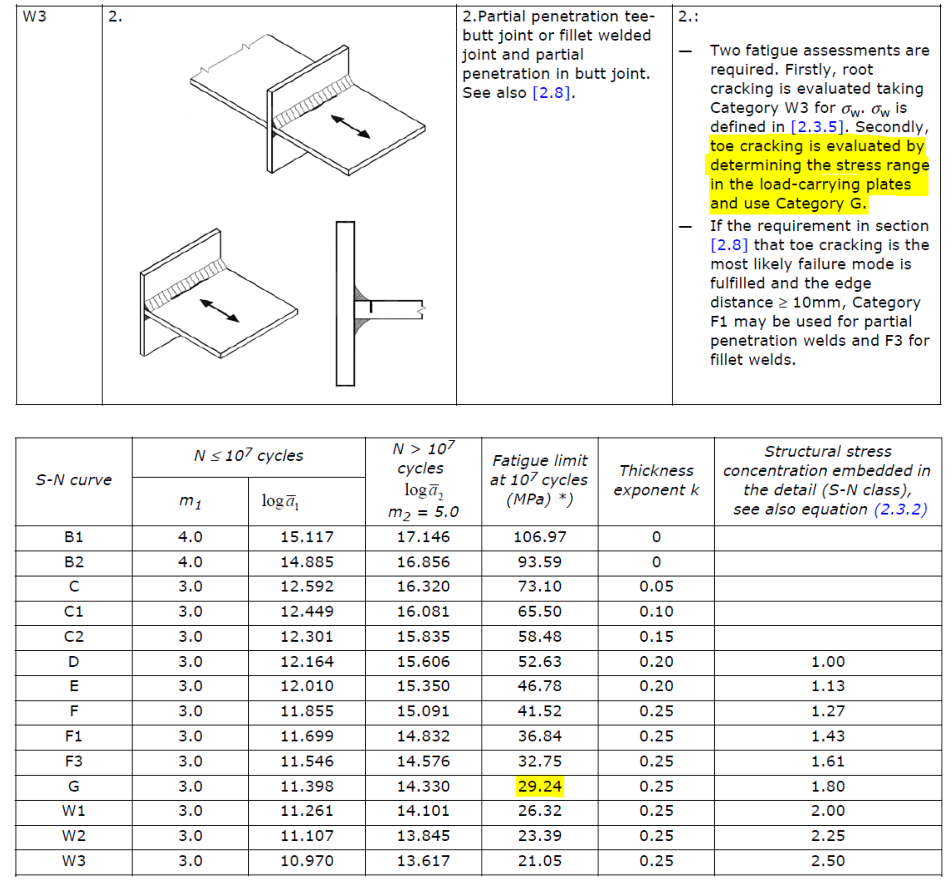
6. 小结和展望
本文讨论了断裂力学分析疲劳的一些重要概念,并结合自身理解说明了其与S-N曲线方法的联系。断裂力学方法因为引入了裂纹长度a,能更好的反应实际裂纹从萌生到扩展,最后到破坏的过程。
诚然,断裂力学计算要比S-N曲线方法要复杂。但同时它也给我们一些启示。在采用S-N曲线方法是我们知道疲劳的结果对应力水平Δσ的高低很敏感。事实上,一些相同(近)设计的船舶和海洋工程,在相似的环境条件下,有些出现疲劳问题,有些没有发生。疲劳发生的“方差”是比较大的。断裂力学的计算表明初始缺陷的取值对结果影响很大。感兴趣可以结合附件中第二个小例子试算,下图的曲线体现了不同的初始缺陷对总循环次数的影响。
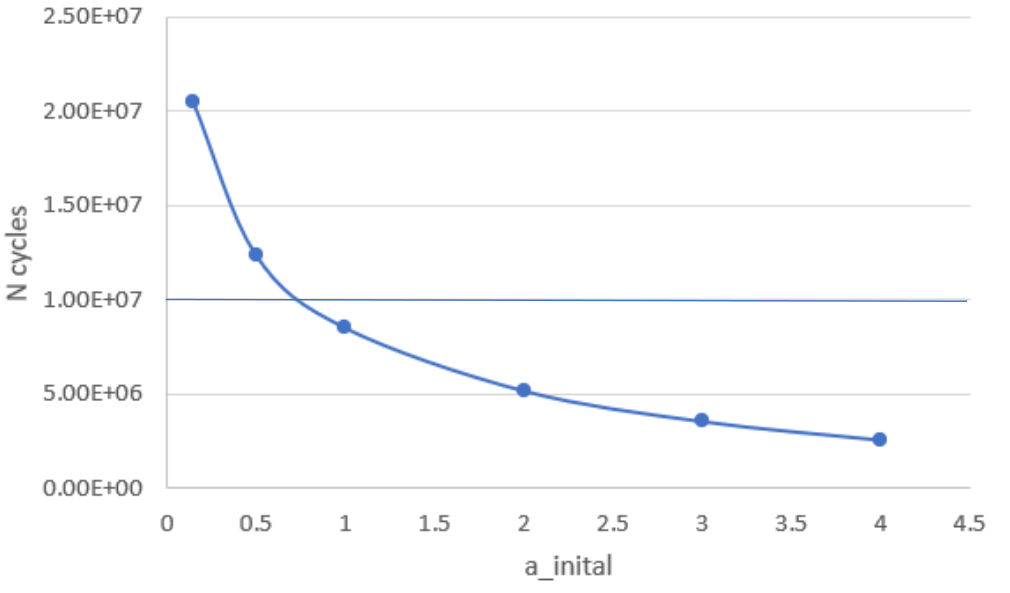
焊接的初始缺陷和设计、建造工艺、建造水平、质量保证及控制(QA/QC)和检验水平都息息相关。可以说只有把它纳入到设计考虑中,我们的疲劳计算才能更接近实际,变得更有意义。
此外,可以预见,当断裂力学方法不断应用,并伴随着建造单位的质量管理不断进步,可能在未来为疲劳强度理性设计和优化提供客观条件。比如漂浮式风机的商业化批量建造,就可能需要断裂力学方法为平台的优化和减重设计提供重要的设计依据。



Python程序1,计算焊接根部root的疲劳循环次数
# -*- coding: utf-8 -*-
"""
Verify RP-C203 Sec2.8
@author: Simon
"""
from sympy import *
from scipy import integrate # input integrate function
import numpy as np
C = 5.21e-13 # mean plus 2 standard deviations
m = 3.0 # Simplified method for single slope curve
sig = 30.0 # G curve stress = 29.24 @ 10^7 cycles
M = 1.0
B = 25.0 # B = tp =25mm
XX = [0.2,0.3,0.4, 0.5, 0.6, 0.7, 0.8, 0.9] # X value for points on curve (2ai/tp)
YY = [0.2,0.5,0.64,0.75,0.84,0.93,1.01,1.07] # Y value for points on curve (h/tp)
N = [] # Record total Cycles/10^7
def I(a):
fwm = (sec(0.5*np.pi*(2*a/W)))**0.5
Mkm = lam0 lam1*(2*a/W) lam2*(2*a/W)**2
Y = M*fwm*Mkm
I = ((np.pi*a)**(m/2)*(Y**m))**(-1)
return I
for i in range(0,8):
h = B*YY[i]
W = B 2*h
lam0 = 0.956-0.343*(h/B)
lam1 = -1.219 6.210*(h/B)-12.220*(h/B)**2 9.704*(h/B)**3-2.741*(h/B)**4
lam2 = 1.954-7.938*(h/B) 13.299*(h/B)**2-9.541*(h/B)**3 2.513*(h/B)**4
II = integrate.quad(I,B*XX[i]/2,W*0.7/2) # a_initial = 2*ai/2, a_critical = 0.7*W/2
n = II[0]/(C*(sig**m))/(10**7) # n= cycle number / 107
N.append(n)
print (N)
# The ratio of cycles is about 1.2, which shows the fatigue life of root is longer than the toe.
Python程序2,计算焊接趾端toe的疲劳循环次数,用于对初始缺陷的敏感性分析
# -*- coding: utf-8 -*-
"""
Sensitive Study on a_initial
@author: Simon
"""
# FM for weld toe on load-carrying cruciform joint
import numpy as np
from sympy import *
from scipy import integrate
C = 5.21e-13
m = 3.0
sig = 30.0 # G curve stress = 29.24 @ 10^7 cycles
M = 1.0
B = 25.0
h = 0.5*B
L = 2*h B
g = B/3 # Typical tapper for P.P.welding
tw = ((B-g)/2 h)*sin(np.pi/4) # P.P. welding throat thickness
a_initial = 1 # initial crack size, typically 1mm
def Mm(z):
return 1.12-0.23*(z/B) 10.6*(z/B)**2-21.7*(z/B)**3 30.4*(z/B)**4 # refer M.4.2 extended surface flaw for a/B <=0.6
def v(z):
if z/B <= 0.073:
return 0.615*(B/tw)**0.5
else:
return 0.83*(B/tw)**0.5
def w(z):
if z/B <= 0.073:
return -0.31
else:
return -0.20
def Mk(z):
if (v(z)*(z/B)**w(z))>=1.0:
return v(z)*(z/B)**w(z)
else:
return 1.0
def II(a):
return (np.pi*a)**(-m/2)*(Mm(a)*Mk(a))**(-1)/(C*sig**m)
N, err = integrate.quad(II,a_initial,0.6*B)
print (np.log10(N))
# For a_inital = 1mm, total cycle N is about 10^6.93





