MATLAB参数拟合
导读
MATLAB的优化工具箱因其完善和强大是优化工作的首选。在做参数反演时,我们通常会结合MATLAB的优化工具箱,这样我们的关注重点就在于问题本身,而不在于花费大把时间在优化算法部分,对优化人员十分友善。因此熟练使用MATLAB优化模块是十分有利的。优化算法有很多,但是下面仅展示使用最小二乘法来对单变量和多变量数据进行参数拟合的两个例子。
单变量参数拟合
用函数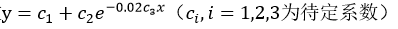 来拟合下列数据
来拟合下列数据
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
y | 3.5 | 3.0 | 2.6 | 2.3 | 2.1 | 1.9 | 1.7 | 1.6 | 1.5 | 1.4 |
优化函数选择lsqnolin,非线性最小二乘法,其官方用法如下:
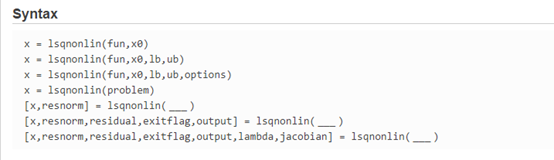
程序实现:
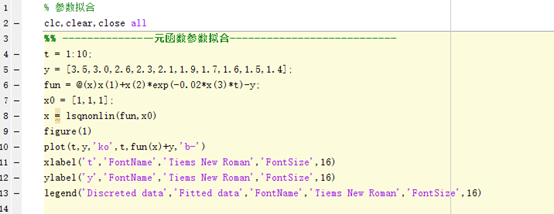
优化结果x=[1.0992,2.9910,11.2454],绘制其散点图和拟合曲线图,两者重合度高,拟合结果是有效的。
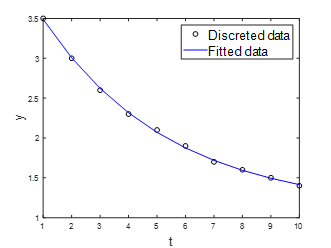
多变量参数拟合
对于多变量函数,进行参数拟合时使用lsqnonlin和lsqcurvefit函数其目标函数创建具有一定差别,如下:
目标拟合函数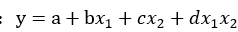 ,其中a,b,c,d为待拟合参数。
,其中a,b,c,d为待拟合参数。
lsqcurvefit函数调用格式:
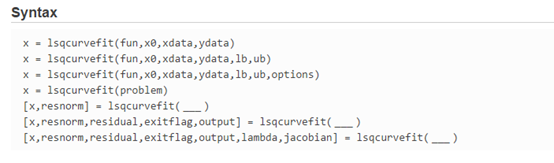
对比lsqnonlin函数的调用格式,发现lsqcurvefit是需要将实验数据作为输入参数,而lsqnonlin则相反。这样输入的差别是前者是直接针对拟合函数进行优化,而后者则是对拟合函数与其实验数据的误差进行最小化的。反映到代码中如下所示:

拟合结果为x=[0.5,2.5,3.0,4.1]同试验函数系数一致,达到了预期效果。对于更多元的函数参数拟合的程序与上述二元函数代码没有本质差别,可直接套用。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2022-04-16
最近编辑:2年前
还没有评论
相关推荐
热门文章




