弧长法简介
本文摘要(由AI生成):
本文介绍了弧长法在处理非线性问题中的应用,特别是针对牛顿迭代法在处理有下降段或极值点问题时的不足。弧长法通过引入约束方程,使迭代求解过程能够平稳地跟踪载荷位移路径,从而有效处理非线性问题中的snap-through和snap-back现象。文中通过一个简单的弹簧杆件结构问题,详细阐述了弧长法的基本原理和迭代格式,并展示了其在求解过程中的有效性。最后,作者指出弧长法在实际应用中的关键在于约束方程的选取和求解细节的优化。
在之前一篇帖子《非线性行为初识》中,我们通过简单的弹簧杆件结构介绍了非线性问题,回顾一下该问题:如图所示,中间节点作用一个F的力,会产生一个位移v, 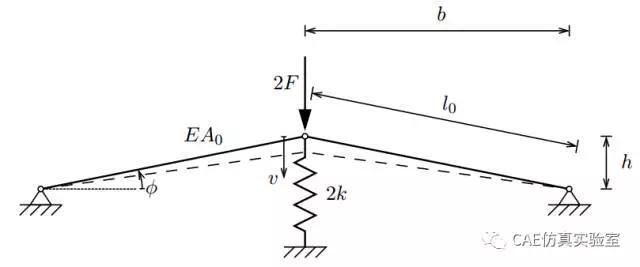
由静力平衡关系可得到

该方程精确解如下,图中不同k对应的曲线,可以看到k比较小时,杆内力起主要作用,呈现出几何非线性,K较大时,弹簧起主要作用,呈现出弹簧的线弹性。
蓝色曲线为精确解,红色点点为固定载荷增量下求得的位移,k=1000时,牛顿迭代法能够很好地跟踪载荷位移路径,得到所有的位移响应。而当k=100时,曲线有下降段,此时牛顿迭代法就没法得到这个区域的位移响应了。
对于下图这样的问题,在拐点处切线刚度为0,在前面的牛顿迭代法中我们是通过给定载荷增量,它已经无法越过极值点得到完整地载荷位移曲线。而且还存在一个载荷对应多个位移,或者一个位移对应多个载荷的情况,很容易发生snap-through和snap-back现象。
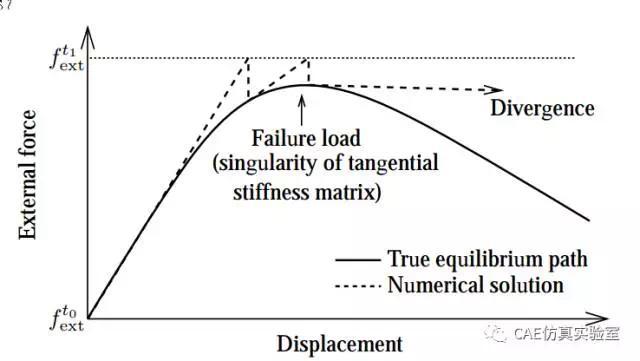
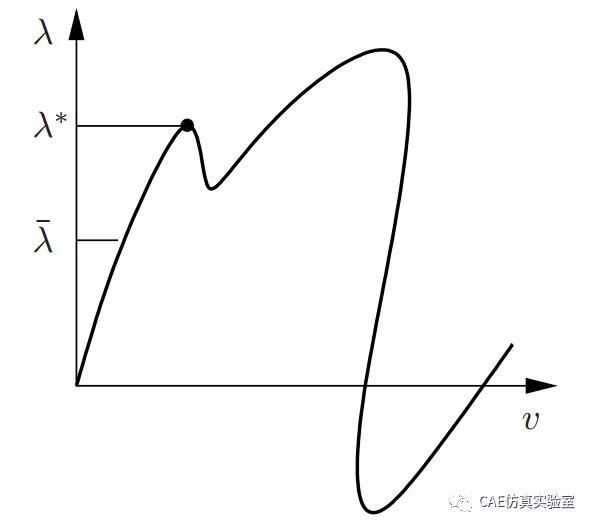
今天就来介绍介绍弧长法,牛顿迭代法在翻过山头延切线方向飞入云霄,直接不收敛。如果让牛顿坐上过山车,那么就能和轨道绑在一起,沿着轨道平稳着陆了。弧长法也是这么做的,通过引入一组约束方程,把迭代求解的过山车,绑定在轨道上,让求解过程能够跟踪载荷位移路径。非线性方程组一般可以表示为:
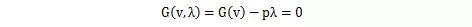
V为位移, 为载荷,加入约束方程f(v,λ)=0
为载荷,加入约束方程f(v,λ)=0
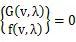
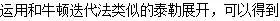
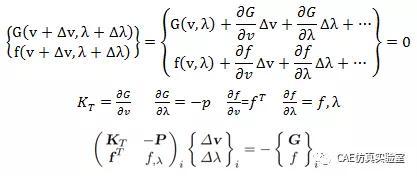
由上式可以得到求解迭代格式:
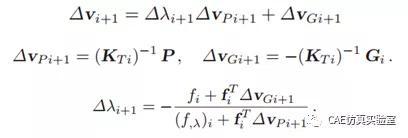
弧长法的图形解释如下,可以看到在一个增量步之中,载荷和位移是同时进行迭代的,载荷增量步也不像牛顿迭代法一样是常数,而是能长能短,能上能下,走得过山峰爬的了坡,因而弧长法有path-following的本领。
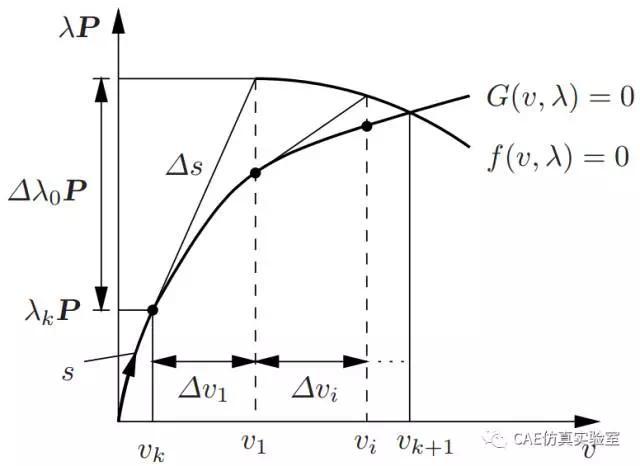
接下来我么采取弧长法求解上面的问题,取如下约束方程:
该函数为一个圆,这更清晰的说明了弧长法的含义,下图为k=0时的载荷位移曲线,除了极值点处有一些不足(代码未加弧长控制),弧长法得到了完整地载荷位移曲线。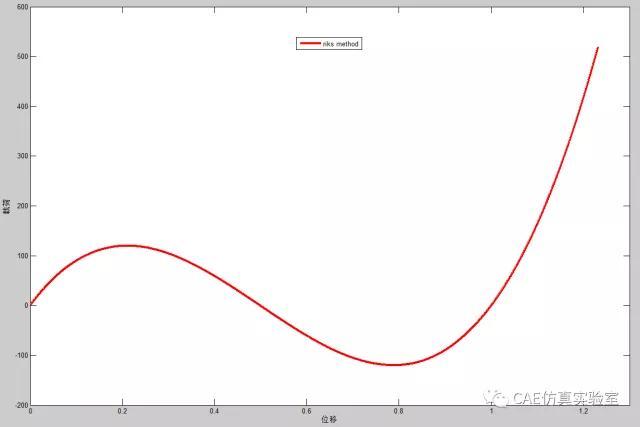
总结:
至此我们介绍了弧长法的基本原理和迭代格式,可以看到,弧长法的基本思路还是较为清晰和简单的,关键是约束方程的选取,和一些求解的细节包括迭代速度优化,弧长选择等问题。这只是一个简单的例子,相信如果大家能够自己动手推推这个公式,自己编写一下代码便会有更加深刻的方法,至于该方法应用到更加复杂的问题和有限元求解格式,还有更多的探讨之处,这里先不考虑。




