基于HFSS和ADS设计一款阶梯阻抗低通滤波器
本文摘要(由AI生成):
本文介绍了基于高低阻抗传输线设计的低通滤波器方法。通过将高低阻抗线级联起来,可以实现低通滤波器的电路效果。文章详细阐述了低通滤波器的设计指标、阶梯阻抗低通滤波器的设计步骤,包括依据技术指标计算滤波器阶数和元件值,确定高低阻抗的特性阻抗值并计算实际结构尺寸,在ADS中创建仿真电路,以及验证电路正确性的方法。同时,还介绍了微带低通滤波器和同轴低通滤波器的设计过程,并强调了考虑传输线不连续性和边缘电容对滤波器性能的影响。通过工程实践验证了设计方法的准确性。
基于HFSS和ADS设计一款
阶梯阻抗低通滤波器
Stone 2022年3月
随着目前高速信息时代的发展,对通信的要求越来越高。与此同时,信号频谱变得越来越拥挤,各种频段的通信系统的相继出现,为了避免各个频段间的相互串扰,高性能的滤波器出现就在一定程度上解决了这个问题。鉴于此,本文采用高低阻抗线的基本原理介绍一款截止频率为3GHz的低通滤波器的快速设计方法,并采用微带线结构和同轴结构分别实现这款滤波器。
1、低通滤波器原理
集总元件低通原型滤波器是现代网络综合法设计微波滤波器的基础,各种低通、高通、带通和带阻滤波器,其传输特性都可依据低通原型滤波器推导出来 。正因如此,才使微波滤波器的设计得以简化,精度得以提高。低通原型滤波器的设计目的就是找到合适的L、C元件值,以满足滤波器的衰减特性。或者使用一个数学函数来逼近理想的低通衰减特性,然后依据这个函数来综合给出各个元件值,即g1,g2到gn.,实际工程中,常用的逼近函数有最平坦低通原型滤波器(Butterworth)、切比雪夫低通原型滤波器(Chebyshev)、椭圆函数低通原型滤波器(Elliptic Function),如图1所示:
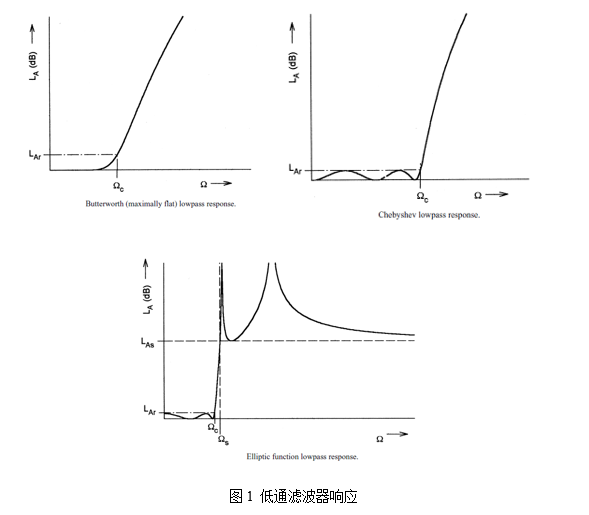
本文基于切比雪夫低通滤波器响应设计了一款截止频率为3GHz的低通滤波器,并采用微带结构和同轴结构来分别实现上述低通滤波器,如图2和图3所示:
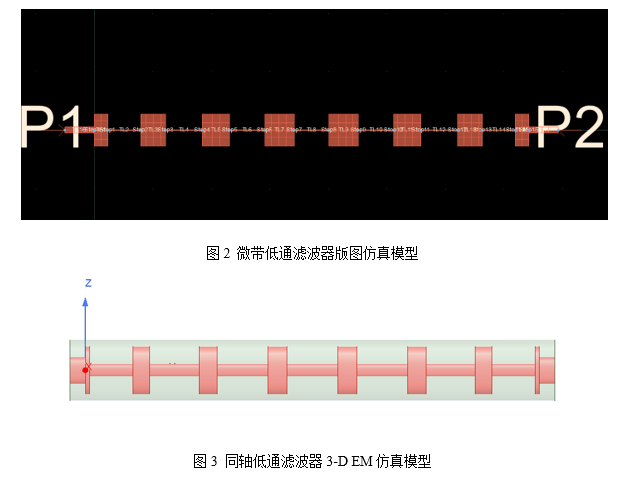
3、高低阻抗线的等效电感与电容
设有一长度为l、特性阻抗为Zo的的传输线,其终端接负载ZL,依据传输线基本原理,其输入阻抗Zin可以表示为下列公式:

由上面两个式子可以看出,当负载阻抗远小于传输线特性阻抗时,传输线端接一个负载阻抗ZL则近似可以看作一个电感和ZL串联。当负载阻抗远大于传输线特性阻抗时,传输线端接一个负载阻抗ZL则近似可以看作一个电容和ZL并联,从而实现低通滤波器中的L、C。
如果分别以ZOH和ZOL表示高低阻抗线的特性阻抗,则等效的串联电感和并联电容元件值和高低阻抗传输线长度关系可近似表示为如下表达式:
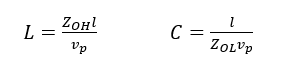
式中l表示传输线的长度,vp表示介质中的波速,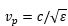 。因此,如果将高低阻抗线级联起来,就类似于低通滤波器电路,如下图4和图5所示。
。因此,如果将高低阻抗线级联起来,就类似于低通滤波器电路,如下图4和图5所示。
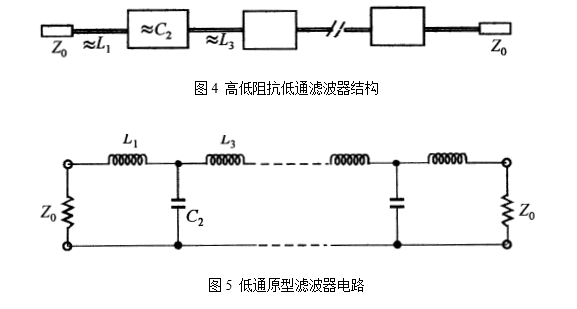
3、低通滤波器设计指标
本文所要设计的低通滤波器技术指标为:
- Frequency Range(工作频率): DC-3GHz
- Return Loss(回波损耗): >15dB
- Rejection(带外抑制): >45dB@3.6MHz
- Impedance(阻抗): 50 ohms
4、阶梯阻抗低通滤波器设计步骤
1)依据指标计算出滤波器阶数和元件值
2)依据低通原型滤波器的元件值确定高低阻抗的特性阻抗值,并计算实际结构的初始尺寸
3)依据计算的初值在ADS中创建低通滤波器仿真电路
4)导入版图仿真或者采用HFSS验证电路正确性
5、微带低通滤波器设计过程
5.1 依据指标计算得到滤波器阶数与元件值。
依据滤波器技术指标,采用切比雪夫低通原型滤波器响应,利用如下公式来计算滤波器的阶数n:

因此若当前所设计的这款工作频率为DC-3GHz的低通滤波器的回波损耗为-15dB,代入公式计算得到n≥14.06,取整数阶数就为n=15。

确定阶数n=15后,就可以通过查表或者采用公式计算的方法来得出低通原型滤波器电路的元件值,计算得到的元件值如下表1所示:

5.2 依据低通原型滤波器的元件值确定高低阻抗的特性阻抗值,并计算实际结构的初始尺寸。
在微波传输中,利用不同特性阻抗的传输线作为半集总参数来实现电感与电容,原则上,高阻抗特性应该尽量高,低阻抗特性应该尽量低。这样就会更加的接近集总参数的特性,但同时也需要兼顾实际加工的可行性。因此,对特性阻抗的取值首先可以按如下公式,并同时考虑实际加工情况,最终在选择Rogers4350B作为设计版材后确定的各个参数如下表2所示:

5.3 依据计算的初值在ADS中创建低通滤波器仿真电路。
在ADS中建立由高低阻抗线级联的微带电路模型,选择Tlines-Microstrip中的MLIN来创建电路,该模型中两个参数需要定义,分别是线宽与线长度,线宽通过前面步骤已经计算获得,线长度可以按1/8波长作为初始值,然后通过ADS中的优化功能快速计算准确的物理尺寸。当然也可以用公式来计算长度的初值,但是相对比较麻烦,同时也需要考虑边缘电容的影响。

在ADS中如图7连接好各个元件,并输入原始1/8波长初始值进行仿真。然后进一步将原理图的参数进行优化,最终原理图优化好后的数据生成版图进行版图仿真验证。
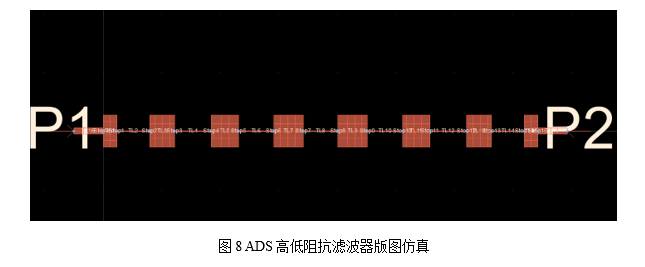
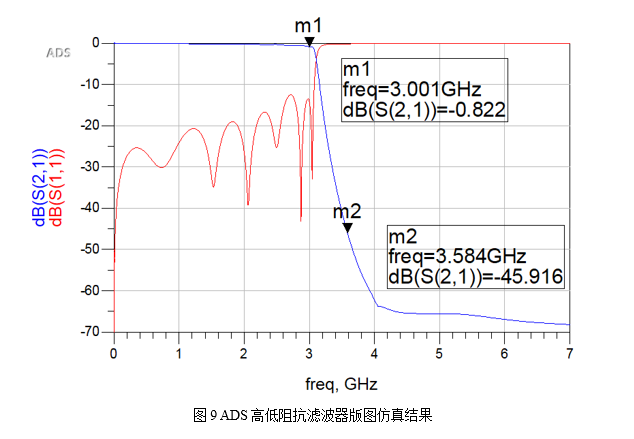
6、同轴低通滤波器设计过程
阶数计算与特性阻抗计算的步骤和前面微带的计算基本一致,这里直接从选定高低阻抗值与尺寸出发。综合考虑实际加工情况与体积大小,选定的同轴线各个尺寸如下表
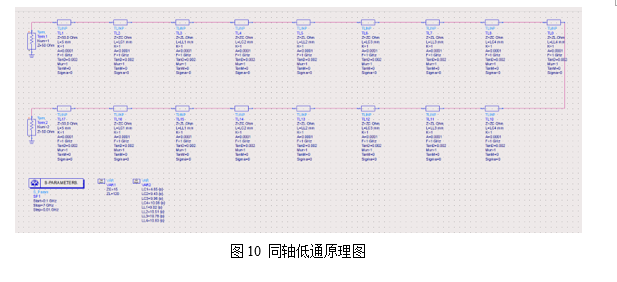
规划好同轴尺寸后,在ADS中使用理想的TLINP来模拟每一节的同轴线,阻抗分别设置为120Ω和15Ω,初始长度可以使用Designer计算出来,创建好的模型如图10所示:
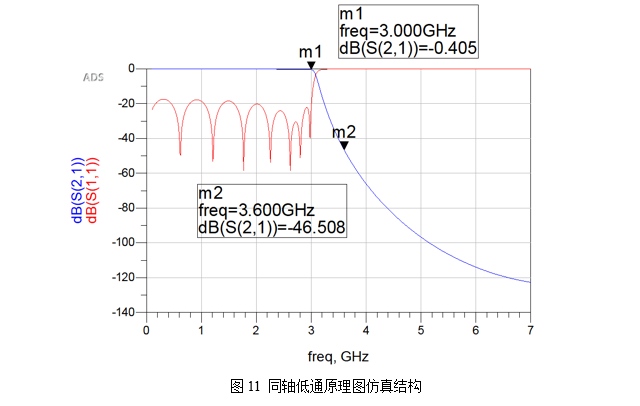
此时运行仿真可以查看得到,Designer中综合的初始尺寸已经能满足当前所设计滤波器的指标,因此当前电路模型不需要进行任何的优化处理。
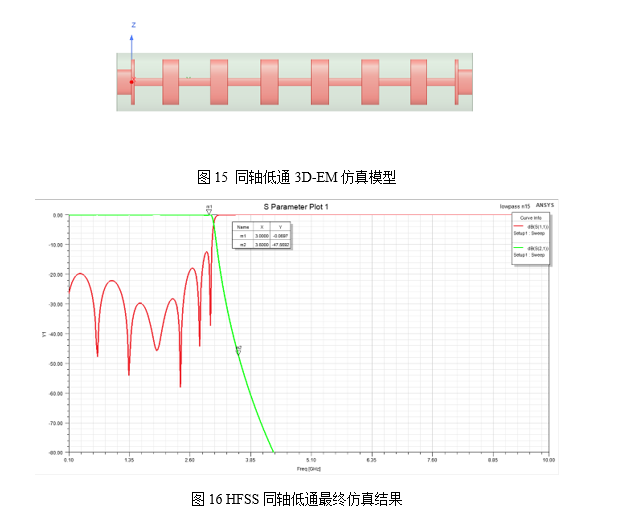
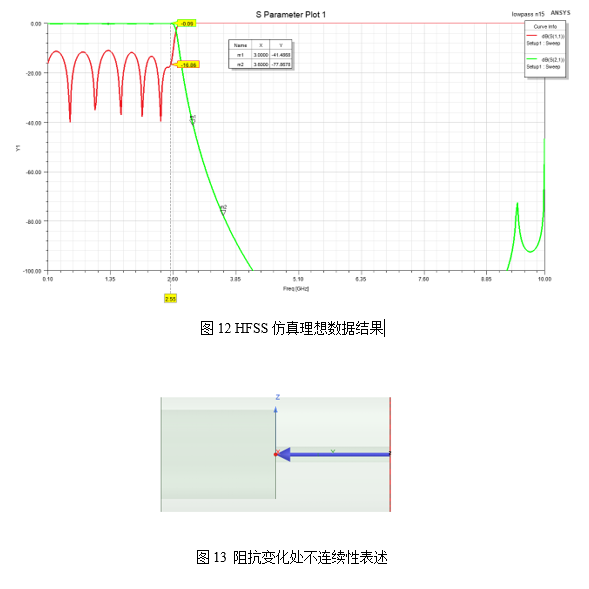
将此时的仿真结果直接导入HFSS中仿真可以看到,HFSS场仿真结果与理论模型的结果相差甚远。主要表现为截止频率过底和回波损耗太差,造成这个原因主要是理想模型中没有考虑同轴内径发生阶跃变化及传输线的不连续性,阶梯处等效一并联电容或称为边缘电容。为了解决这个问题,可以在HFSS中建立如图13所示模型,获取模型的S2P文件,这个文件就可以准备的表述高低阻抗不连续处的各种影响。
将这个S2P文件导入ADS中对模型进行再次仿真可以查看得到,ADS中理想模型的数据和HFSS数据基本一致。

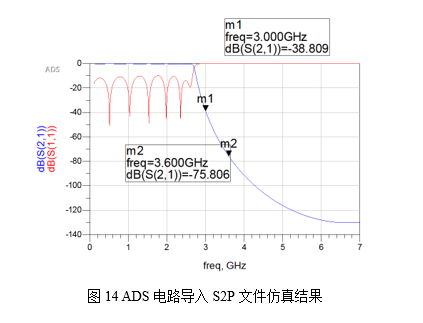
此时可以看出,由于电路模型加入了不连续性表述,理论模型与HFSS场仿真模型能够完全对应,因此,只需要在ADS电路中将模型的数据优化到当前滤波器的指标就能完全设计出同轴低通。经过多次工程实践,证明此方法的准确性。