有限体积方法处理非结构网格-多边形和多面体的几何的处理
上一篇文章中已经讲了通过离散求解的流程,目的就是先构造出每个网格的代数方程,代数方程的具体形式如下,碰到的问题就是需要求解三个系数项bc,af,ac
但是这三个系数项就是采用有限体积方法离散获取的,每个都有自己的特点, 有的需要当前网格的值或者这个值的梯度,有的需要与当前网格相邻的单元的值。而且前面也列出了这三个公式的具体表达式,如下
![[公式]](https://public.fangzhenxiu.com/fixComment/commentContent/imgs/1645200420453_9owjqk.jpg?imageView2/0)
前面我们已经知道求解这三项只需要知道gDiff和Tf还有▽ϕ三个就可以了这三个就可以了,而且这三相都是和网格相关的,而且都需要长篇大论的写,所以我们就一个一个的处理,首先是这个gDiff吧,先给出一个网格的图片,图片来自互联网哈。
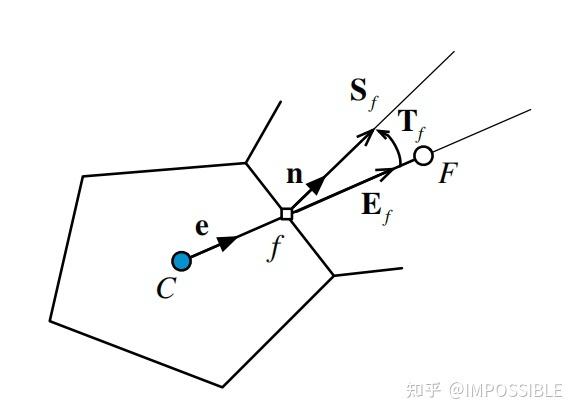 一个典型的非结构网格
一个典型的非结构网格
这里把公式先写出来
Ef是表面向量的类正交扩散分量,dCF是两个单元的质心距离,e是两个网格单元质心向量的单元向量,Sf是面的法向向量,已经知道的是网格中所有的点的坐标都。
首先来完成单元的质心计算吧,当然质心的计算其实也是一个比较漫长的步骤,首先是把每个面的面心计算出来,对于三角形来说每个面的面心直接加权就可以,但是对于多边形来说还需要转化为三角形再处理。
1.大致流程是这样的,通过面上的顶点坐标加和然后除以顶点的数目可以计算到几何中心
2.将几何中心与边上的两个点相连得到n边形对应的n个三角形
3.将这n个三角形的面矢量和面积分别计算出来,还有三角形的几何中心
4.将这n个三角形的几何中心和对应的面积加权就可以得到面的面心,三角形面积矢量加和除以2就是这个面的面积矢量Sf。
为了省去你的麻烦,我把函数已经定义好了,当然你也可以自己编写,最好以类的形式写出来,计算结果也存为类里面的属性,可以减少计算量。
"""Created on 2022/1/25 10:45@Author: 123@Email: 985040320@qq.com@Describe: **加入文件描述, 要实现的功能, 注意事项等**""" def face_center_and_area(vertices):#传构成这面的点的列表 # 计算k个点组成的多边形的几何中心 size = len(vertices) geo_center = np.sum(vertices, axis=0) / size face_total_area = 0.0 face_normal_vector = np.zeros((3,)) face_centroid = np.zeros((3,)) # 形成三角子面. # 每一个面都是以边作为基础,以面的几何中心作为顶点然后重建 for i in range(len(vertices)): # 计算子面的点 p1 = vertices[i] p2 = vertices[(i 1) % size] p3 = geo_center # 计算子面的几何中心 subface_geo_center = np.sum([p1, p2, p3], axis=0) / 3.0 # 计算子面的面积和面向量,三角形面积等于面矢量的模长除以2 sf = np.cross((p2 - p1), (p3 - p1)) area = np.linalg.norm(sf) / 2.0 # 计算多边形面的面积和面矢量 face_normal_vector = sf face_total_area = area face_centroid = face_centroid (area * subface_geo_center) face_centroid /= face_total_area face_normal_vector /= 2.0 return face_centroid, face_total_area, face_normal_vector
可见通过上面的四个步骤,我们由点的坐标计算出了面的面积,面心,面心矢量。
面解决了,接下来就是计算体心了,类似于多边形转化为三角形再进行向量求面积,求面心,求面矢量,多面体需要转化为像金字塔的多面体(底面的面积面矢量,面心都已知)之后再进行质心的计算
1.首先由上面的面心计算多面体几何中心,直接加取平均即可
2.通过这个几何中心和各个面的面心(上一步计算给出的)可以构造一个多面体并计算出他的质心(在基面和几何中心的0.25处),这里通过面矢量和这两个点也可以顺便把这个有点像金字塔的几何的体积同时求出。
3.体积加和就是整个网格的体积,第二部求得的质心进行对应的体积加权就可以得到网格的质心。
"""Created on 2022/1/25 10:45@Author: 123@Email: 985040320@qq.com@Describe: **加入文件描述, 要实现的功能, 注意事项等**""" def cell_center_and_volume(faces):#传入面的列表 # 计算单元的几何中心,就是简单的采用所有点的进行平均值计算 geo_centeroid = np.zeros((3,)) for face in faces: geo_centeroid = face_center_and_area(face)[0] geo_centeroid /= len(faces) # 根据每个网格面和几何中心创建类似金字塔的多面体 element_volume = 0.0 element_centroid = np.zeros((3,)) for face in faces: face_centroid, face_area, _ = face_center_and_area(face) # 四面体的中心落在基面和几何中心距离的0.25处 pyramid_centroid = (0.75 * face_centroid) (0.25 * geo_centeroid) pyramid_volume = (1.0 / 3.0) * face_area * np.linalg.norm(face_centroid - geo_centeroid) # 借助四面体的中心计算几何体的体积 element_volume = pyramid_volume # 所有的面计算完成之后用用对应的体积去加一个权 element_centroid = (pyramid_volume * pyramid_centroid) # 最后计算体积加权网格中心 element_centroid = element_centroid / element_volume return element_centroid, element_volume
看现在网格的质心已经求出来了,dCF是两个单元的质心距离就是这两个点构成的向量的模嘛,e就是这两个点构成的向量再除以这个模嘛,sf就是这个面对应的面矢量嘛,所以就可以计算gDiff了。
现在就已经完成了gDiff和Tf还有▽ϕ三个中一个系数的获取,是不是就是通过网格的拓扑关系获取的。后面再依次来处理剩余的两个,同样还是通过网格的拓扑结构。




