scipy求解常微分方程组

Scipy求解常微分方程组有scipy.integrate.solve_ivp和scipy.integrate.odeint，后者是较老的版本主要是采用 FORTRAN 的odepack库里面的lsoda 方法，而前者是后面更新的函数，支持的方法也更多，按照官方的文档介绍大致有如下的方法。

scipy.integrate.solve_ivp内可用的数值积分方法

函数的调用形式如下scipy.integrate.solve_ivp(fun,t_span,y0,method='RK45',t_eval=None,dense_output=False,events=None,vectorized=False,args=None,**options)

下面以几个例子进行说明首先是如下的简单形式，设初始值为0

import matplotlib.pyplot as pltfrom scipy.integrate import solve_ivpplt.rcParams['font.sans-serif'] = ['Microsoft YaHei']def fun(t, y):
    dydt = [1]
    return dydt# 初始条件y0 = [2]yy = solve_ivp(fun, (0, 5000), y0, method='Radau')t = yy.tdata = yy.yplt.plot(t, data[0, :])plt.xlabel("时间s")plt.legend(["求解变量"])plt.show()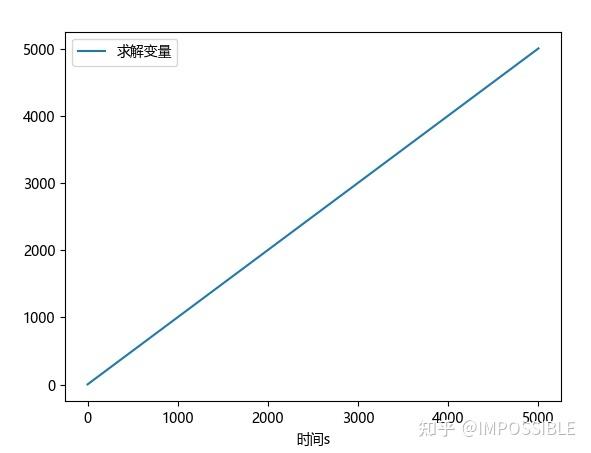

然后逐渐复杂一点，假设方程为

发现得到的结果是这样的，很明显不合理

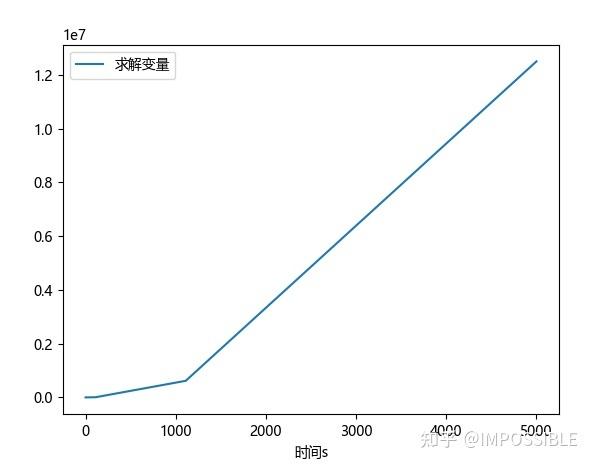
这是因为求解的时候输出的插值的问题，我们改一下代码，结果如下

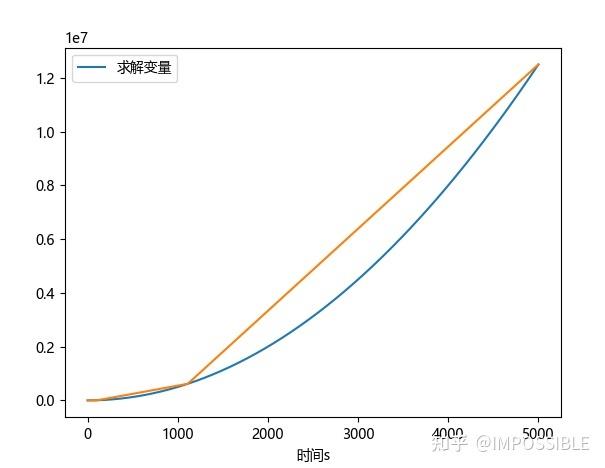
是不是就合理多了

完整的代码如下

import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
import numpy as np
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']

def fun(t, y):
    print(t)
    dydt = [t]
    return dydt

# 初始条件
y0 = [0]

yy = solve_ivp(fun, (0, 5000), y0, method='Radau',t_eval = np.arange(1,5000,1) )
xx = solve_ivp(fun, (0, 5000), y0, method='Radau')
t = yy.t
data = yy.y
t2 = xx.t
data2 = xx.y
plt.plot(t, data[0, :])
plt.plot(t2, data2[0, :])
plt.xlabel("时间s")
plt.legend(["求解变量"])
plt.show()

现在看着还不高端，可以多定义两个函数让他看起来更高端一些，方程如下

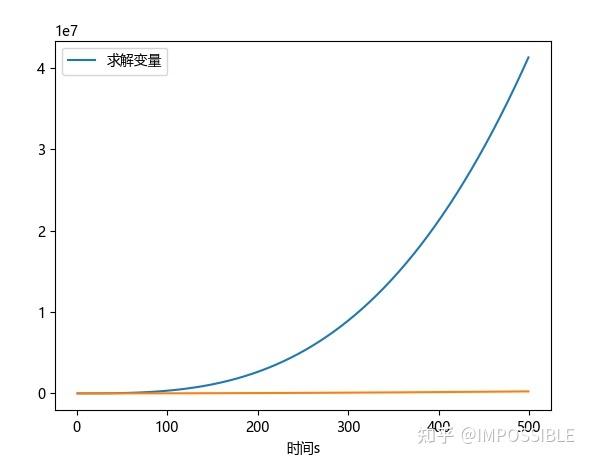
代码如下

import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
import numpy as np
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']

def fun(t, y):
    y1 = y[0]
    y2 = y[1]
    dydt = [y2, t*t-y2 t]
    return dydt

# 初始条件
y0 = [0,1]

yy = solve_ivp(fun, (0, 500), y0, method='Radau',t_eval = np.arange(1,500,1) )
t = yy.t
data = yy.y
plt.plot(t, data[0, :])
plt.plot(t, data[1, :])
plt.xlabel("时间s")
plt.legend(["求解变量"])
plt.show()