海洋平台防爆墙结构分析
引言:
海洋平台不仅要能抵御恶劣的海洋气候环境,还要能够抵御各种意外载荷(Accidental Load)。尤其是油气钻探、开采、生产类的海洋平台,由于不可避免的存在危险气体泄漏的风险,火灾和爆炸载荷是其结构设计中必须考虑的因素。

Deepwater Horizontal explosion(2010)

Piper Alpha explosion(1988)
防爆墙结构:
海洋油气平台就像一座海上化工厂,其“占地”面积寸土寸金,作业区、生活区、储物区密集布置,很难做到像陆地上的距离分隔。为了保护人员安全和关键核心设备,设置防爆墙结构成为重要的防护措施。规范中,把防爆墙定义为safety critical structural element,经常被布置在生活区之前,同危险作业区隔开。
防爆墙结构设计思路有别于一般的结构设计,主要有三点:
- 防爆墙结构不应作为承重墙,由大结构支撑
- 防爆墙结构设计主要考虑是“吸收”爆炸能量,而不是硬碰硬的“抵抗”。能量主要转换为塑性变形能和振动耗散。
- 防爆墙结构应该简单、轻质且易于维护。控制防爆墙的重量对平台整体重量控制十分重要。
槽型结构由于结构形式简单、结构利用率高和良好的延展性,成为防爆墙中最常见的结构形式。
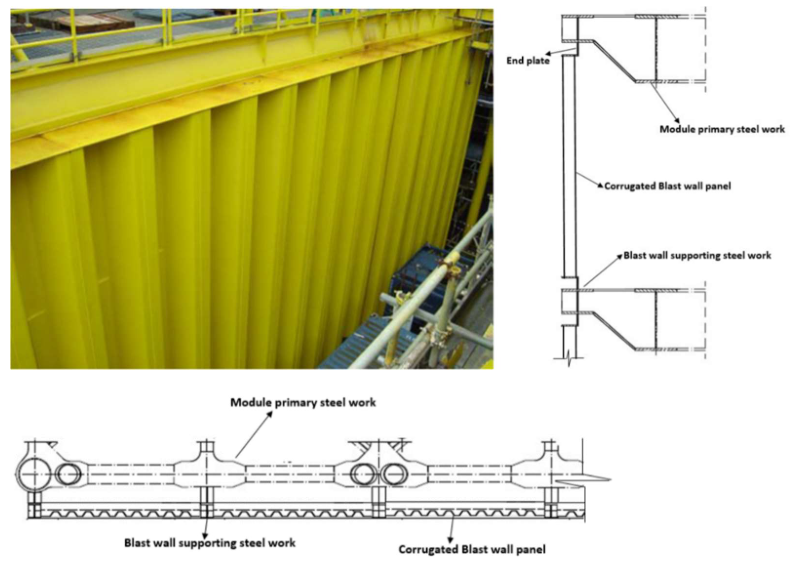
爆炸载荷:
英国HSE规范(Interim Guidance Notes for the design and Protection of Topside Structure against Explosion and Fire,后简称其为Guidance)对爆炸载荷给出了比较具体的介绍。爆炸载荷一般可模拟为一个三角冲击载荷,其重要参数为Peak Pressue,Rise Time和Duration τ。由于τ很短(40~100毫秒量级),与结构的固有周期接近,τ和结构的固有周期T之比是重要参数。
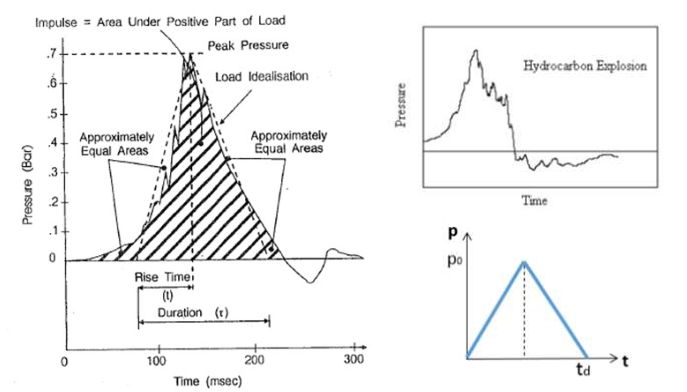
Guidance中对这类结构动态响应有如下分类,大家可以对号入座。

工程案例:
了解了结构形式和载荷,小伙伴们肯定跃跃欲试要上仿真有限元工具做分析了。前面提到了,防爆墙要能通过塑性变形能来吸能,而且这个过程属于瞬态或动态响应,这个分析是有一定挑战的。如何分析结果是靠谱,如何判断趋势,笔者认为有些难度。
这里笔者用一个典型的工程例子,介绍一下经典的梁分析和等效单自由度系统(SDOF)分析的方法,作为有限元仿真的辅助,和非线性有限元的结果作对比。文章最后还提供了一个Python的小程序实现(由于涉及迭代,不得不编个程),供大家参考讨论。
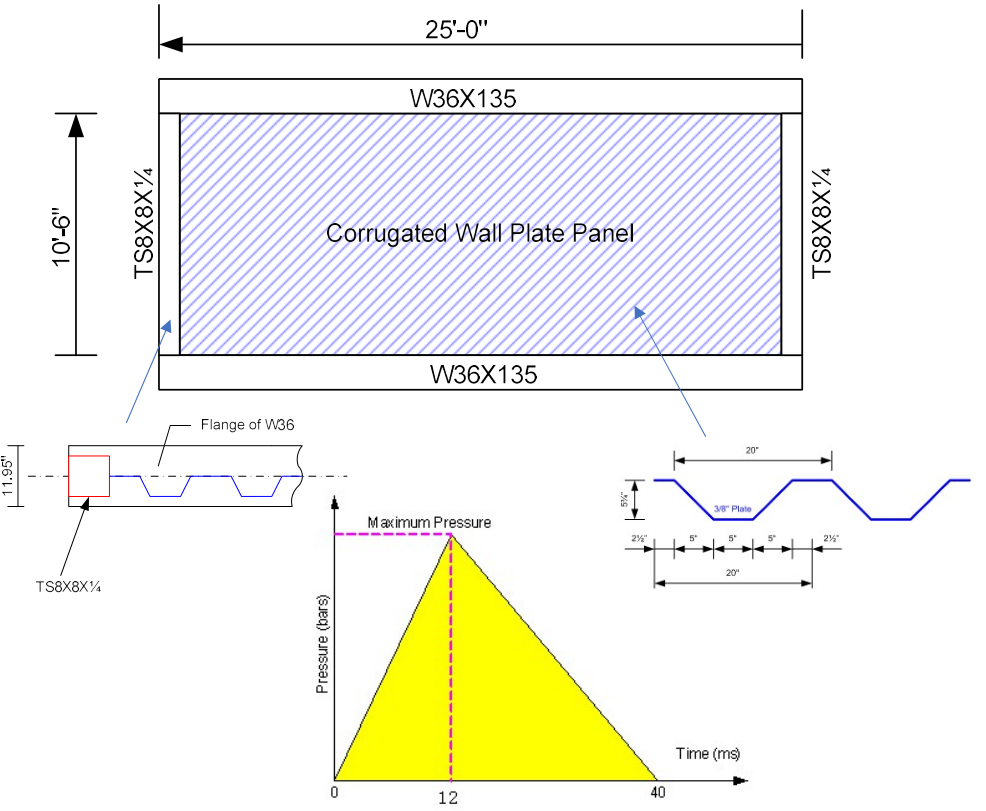
经典梁分析与等效SDOF
做结构分析,一般首要关注结构的最大响应(最大位移/变形,最大应力、应变等)。这非常适合用Guidance中图谱设计的方法,下面简述其过程。
1. 建立经典梁
我们可以把槽型舱壁简化为竖向的简支梁,梁的截面为一个槽型。Guidance中给出了经典梁到等效SDOF系统的转化的参数,注意这里的参数分为弹性部分和塑性部分。经典梁和等效SDOF系统具有相同的固有周期和最大位移响应(梁跨中)。
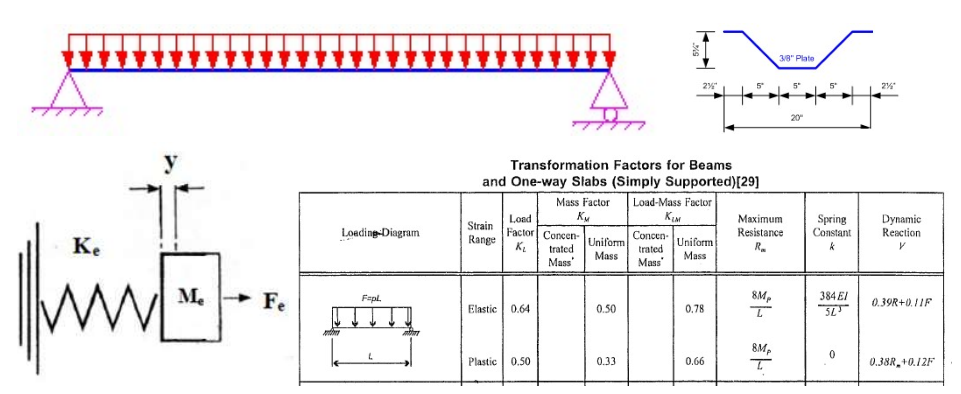
2. 固有周期T计算
在弹性阶段,固有周期T = 2π(KLMe ▪ Mt/kE)0.5
其中,Mt为总质量。KLMe为弹性load-mass系数,等于0.78。kE为SDOF的等效刚度,与梁的截面属性有关(即梁跨中柔度的倒数)。
由简支梁的弯矩分布可知,梁的跨中弯矩最大,梁发生塑性变形的标志为梁跨中形成“塑性铰”。工程上可以这样简化,即认为塑性铰一旦形成,SDOF的刚度降低为0。SDOF弹簧能产生最大的反力为Rm=8Mp/L。Mp为塑性铰弯矩。SDOF系统的刚度曲线如下。
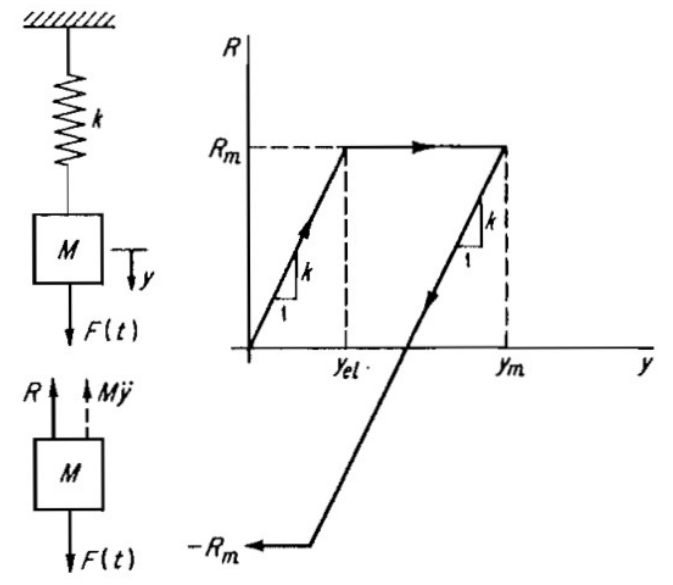
为了衡量结构进入塑性的程度,定义SDOF系统的弹性位移极限为Yel。定义SDOF系统最大位移Ym与之比为ductility ratio μ=Ym/Yel。
从弹性进入塑性阶段,固有周期T = 2π(KLM* ▪ Mt/kE)0.5。其中,KLM*为“平均”的load-mass系数(本例中KLMe = 0.78,KLMp = 0.66):
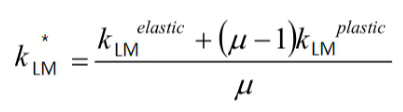
可以看出固有周期T是μ的函数,分析中塑性部分需要迭代计算。
3. 图谱设计得到最大响应(迭代得到μ)
本例中,在弹性范围内,结构的固有周期T约为21.5ms,td=40ms,raise time =0.3td,td/T=1.86。从线性系统动力系数图(Dynamic Load Factor)可知,动力系数约为1.65。其物理含义是在弹性范围内动载荷的作用下,位移响应约为静载荷的1.65倍。
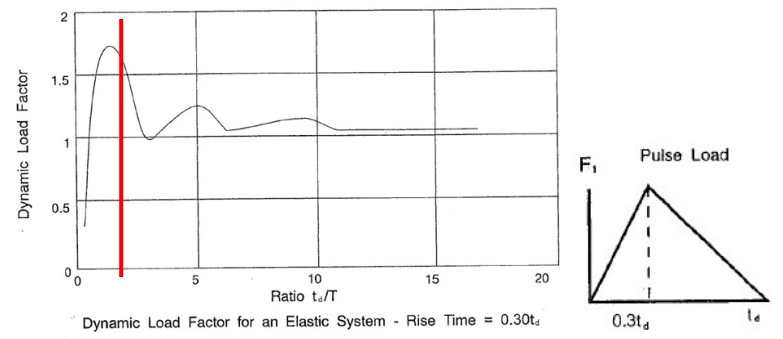
在本例中,结构的弹性变形极限为15mm。载荷峰值F1作为静载荷时的弹性变形为16mm。可以认为Rm/F1≈1.0。
考虑动力放大效应,结构响应将“放大”,进入塑性,且最大变形应大于1.6。通过Guidance中的设计图谱,可以估计μ在1.8~2.2的范围内。
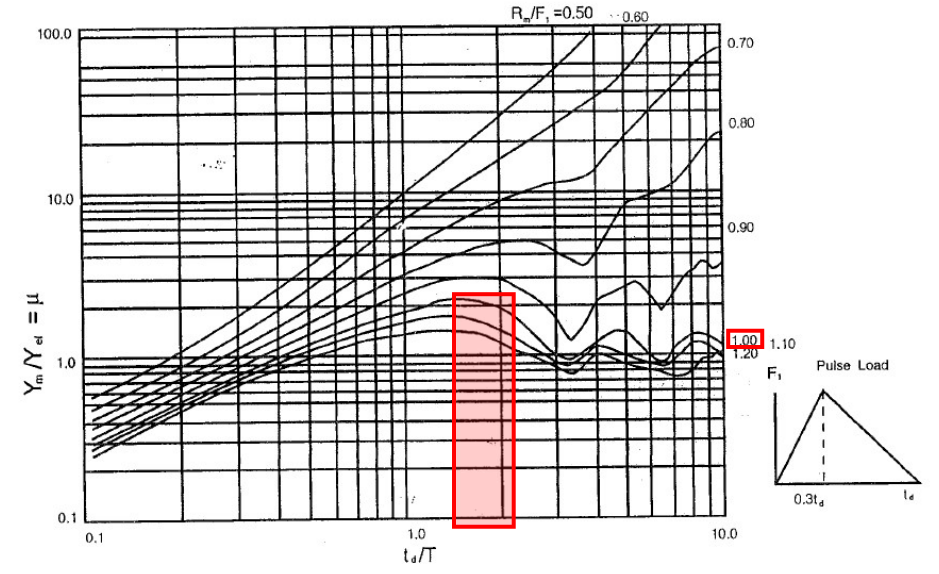
迭代思路:

迭代计算的结果μ = 1.99, 本文最后附Python迭代小程序。
非线性有限元分析
终于轮到大杀器非线性有限元上场了。有了上面的估算,我们是不是对结果已经有了一定的预期呢?这里对于非线性有限元计算的过程分析不再过多展开了,用理想弹塑性材料,施加载荷时历,选取足够小的时间步长进行瞬态分析。我们直接看结果。
最大位移为32mm,μ =32/15=2.13:
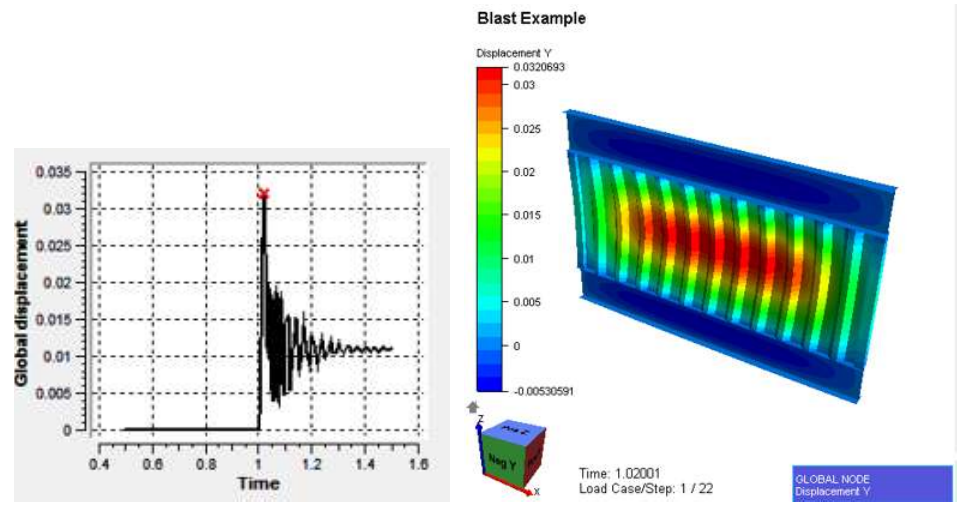
最大响应时的塑性应变和响应最后的残余塑性应变:
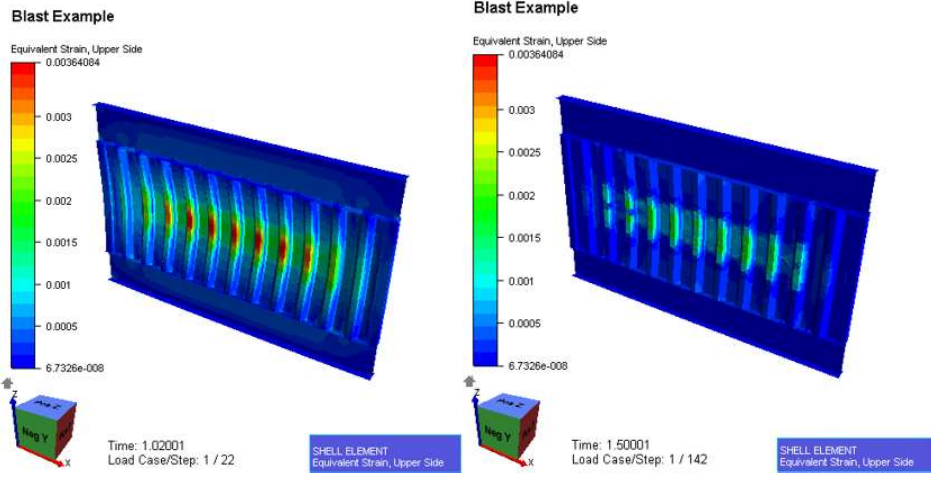
从结果看,梁分析和等效SDOF系统对结构最大响应的预报是比较准确的。而μ值还有较大提高的空间(一般μ可在5~10的范围),说明防爆墙的结构可以优化(如用小一点的板厚)。这一步可以在等效系统里调整参数很方便快速地缩小最优解的目标范围,再通过非线性有限元来验证和控制应变。这样可以提高工作效率,让有限元发挥出更大的效用。
需要强调的是,这类问题做有限元分析是十分有必要和有优点的,体现在:
1. 在基本解的基础上,可以考察更复杂的因素,如材料的动力硬化、爆炸载荷的“负压”阶段、剪切的影响、“膜”应力的影响、边界条件的影响等等。
2. 可以更真实的反映结构整体的刚度和相互作用,尤其是槽型壁各槽条之间多样的模态形式。这是简单梁和等效SDOF系统难以考虑的。
3. 可以更直观的检查塑性应变和范围。塑性应变是衡量结构是否仍然有效的重要衡准。一般焊接处控制在5%以内,非焊接处在10%左右。
4. 可以结合更高级的CFD流固耦合计算得到更为接近实际的载荷时历,进一步优化设计。
当然敏感性分析是不可缺少的,比如网格类型、网格大小、系统阻尼设置(对于本问题求瞬态最大响应来说,阻尼应该不是主要问题)等等。
小结
本文通过一个实际工程案例,介绍了防爆墙从梁分析到等效SDOF系统,再到nonlinear FEA的分析过程。笔者一直认为FEA仿真的第一步,也许是最重要的一步,那就是抛开FEA的对仿真结果的事先估计。无论估计的正确与否,都会给仿真人员带来收获和提高。
希望本文能抛砖引玉,供广大仿真同仁讨论参考。关于结构动力学,推荐一本好书: Intro to Structural Dynamics,JOHN M. BiGGS。
另外,笔者最近会推出一门课程《海洋平台强度分析》,更多类似的分析方法和Python程序将在课程中讨论,欢迎大家关注,一同学习、进步。
# Python Code
import numpy as np # Python强大的numpy模块搞定基本函数
from scipy import interpolate # Python强大的scipy模块搞定插值
# 定义设计曲线 (Rm/F1=1.0)
# List x=td/T
# List y=Ym/Yel
x=[0.11312,0.17313,0.2571,0.4074,0.58394,0.79807,1.0504,1.3964,
1.773,2.3566,2.685,3.0976,3.3961,3.7356,4.2567,4.8228,5.6064,
6.2329,6.5401,6.8434,7.2125,7.8135,8.7628,9.8677,]
y=[0.29923,0.45155,0.6526,0.9747,1.2727,1.5763,1.834,2.1859,2.1054,
1.5665,1.2086,0.946,0.9265,1.0447,1.2724,1.3661,1.0901,0.9006,
0.8756,0.9799,1.122,1.2672,1.3025,1.1459,]
# 定义二次样条插值函数
f=interpolate.interp1d(x,y,kind='quadratic')
# 定义基本参数
td=0.04
KLM_e=0.78
KLM_p=0.66
Mt=154
k=10233662
# 定义初始迭代的u
u=1.8
# 定义迭代函数
def iteration(u_old): # define iteration function
KLM = (KLM_e (u_old-1)*KLM_p)/u_old
T = 2*np.pi*(KLM*Mt/k)**0.5
tau = td/T
u_new = f(tau)
return u_new
# 调用循环体来迭代
while True:
UU = iteration(u)
if np.abs((UU-u)/u)<=0.001: # Set 0.1% as criteria
break # stop iteration if criteria is fulfilled
else:
u = UU # update u and continue the iteration
continue
print (u) # 打印结果,u=1.99





