What's new | Cradle CFD V2022 新功能展示(Part 2)

本文摘要(由AI生成):
本文介绍了在scFLOW V2022中进行螺旋桨空化的LES/DES分析的方法,并比较了三种空化模型的结果。此外,文章还介绍了scFLOW中的DEM功能增强,包括滚动摩擦阻力模型的改进以及新的滚动阻力模型的应用。文章还通过多个案例展示了scFLOW在颗粒流模拟、非牛顿流体分析以及LES计算等方面的应用。这些案例包括休止角模拟、贯入试验仿真、巴西坚果仿真、泥石流防护网模拟、非球形颗粒混合以及剪切变稀流体中气泡的上升等。通过这些应用案例,展示了scFLOW在流体和颗粒流模拟方面的强大功能和准确性。
Cradle CFD近期迎来了V2022新版本,小编将分三期为大家详细讲解并附上Demo展示,上期回顾:scSTREAM V2022 新功能。本期内容为:SCFLOW v2022 新功能概述。
SCFLOW v2022 新功能概述
前处理
求解器
SCFLOW v2022 新功能详细介绍
1 面组成的计算域
- 可以通过指定零件的曲面来创建符合零件形状的面零件。
- 当零件表面上有薄板零件时,防止薄板零件从零件表面去掉。
- 指定在其上创建图纸零件的零件曲面,并创建衍生图纸的曲面区域。
目标:带有薄零件的模型。

2 voxel-fitting支持面组成的域
- 薄板零件可以在体素拟合网格中进行处理。
- 减少薄零件的网格数量,提高网格质量。
- 使用体素拟合网格器对包含面零件的模型执行网格划分。
目标:存在面零件的模型。

3 指定零件的坐标
通过使用体素拟合网格器进行网格划分将零件分割为多个闭合体积时,可以通过将指定零件的坐标指定给闭合体积来为每个闭合体积设置不同的材质。
好处:
使用体素拟合网格器对每个闭合体积进行轻松的材质设置。
创建坐标指定的零件,该零件链接到闭合体积,并将材质设置为该零件。
目标:
将一部分计算域划分为多个闭合体积的模型。

注:仅当使用体素拟合网格器时,才能使用坐标系指定的零件。
4 将实体材质设置为多面体网格的空心区域
What:
- 实体材质可以设置为建筑分析模型创建的空心区域。
Benefits:
Where:
- 当通过构建分析模型创建许多空心区域时,通过向空心区域提供实心材料来稳定计算。
- 以与普通材质设置相同的方式将“实体材质”设置为“空心区域”。
- Target:
- 创建空心区域的模型.

5 体素拟合网格的完全分布式并行化
What:
Benefits:
Target:

6 压缩GPH文件
包含5000万个网格的GPH文件
未压缩 5.4 GBytes
压缩 1.5 GBytes

7 高超音速流动分析
What:
- 高超音速解算器是现有基于密度基求解器的扩展,专门用于高速流动。
Benefits:
Target:
- 现在支持高超音速区域(马赫数>5)的热化学非平衡流。.
- 对理想气体无法处理的物理现象进行高温高速分析
- 稳健而准确的分析方法,即使在高马赫数流量下.
- 以高超音速飞行的大气层返回舱和其他物体

案例1:高超流动(马赫数=8.98)
5 组分, 17 反应
在这两种情况下都考虑了催化壁效应
在高超声速下不仅可以准确地预测气流,而且可以准确地预测传热现象。

案例2:FIRE II 太空舱再入模拟
本案例模拟FIRE II舱在马赫数35.7 下的飞行试验。

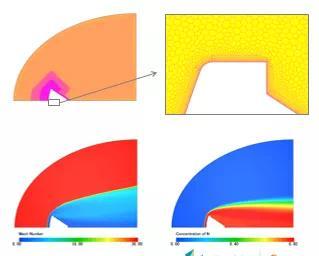
反应: 5 种组分 (N2,N,O2,O,NO)
环境:假设振动能量温度相同
温度: 242[K]
静压 : 16.7[Pa]
物质: Air (Mole fraction of 0.79 of N2 & 0.21 of O2)
壁面表面温度: 1325[K]
8 密度基求解器功能增强
(1)并行加速
除了MPI并行,还可以使用线程并行来执行高速计算
滚动摩擦阻力模型的改进-对应非球状模型
(2)支持不可压缩流动
What:
基于密度基求解器专门用于可压缩流,也支持不可压缩流。当前版本无法同时解决可压缩和不可压缩问题,但在未来版本中将支持此版本.
Benefits:
它是一个耦合求解器,即使由于复杂的单元变形等原因导致单元质量差,也可以稳定地计算。
它具有良好的并行效率,并且还可以实现线程并行。
在未来的版本中,将有可能同时处理不可压缩流体,同时准确捕获带有冲击波的可压缩流。.
在更宽的流动区域中,除了默认的基于压力的解算器之外,我们还可以有其他选择。基于密度基求解器具有以下特点,预计将广泛使用:
Target:
各种热流体分析,如车身的空气动力学分析
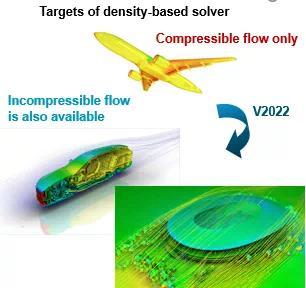
案例 :简化车辆模型
汽车工程师学会简化车辆模型的验证案例(JSAE)
针对JSAE Benchmark, 采用压力基求解器和密度基求解器,用同一套网格进行分析。
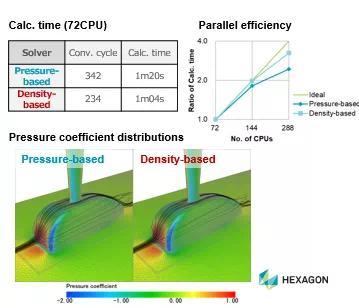

计算条件:
Fluid : Incompressible
Analysis type : Steady-state
Turbulence model : RANS with SST k-ω model
No. of elements : 1.18 million
守恒设置条件一致.
在这个问题中,基于密度的解算器收敛速度更快,计算速度也更快。
并行效率在基于密度的解算器上显示了更好的性能:并行数越多,速度越快。
9 粒子破碎模型
新版本支持VOF转换为颗粒相分析。由此可以用粗网格,高精度计算液滴破碎,并减少计算时间。
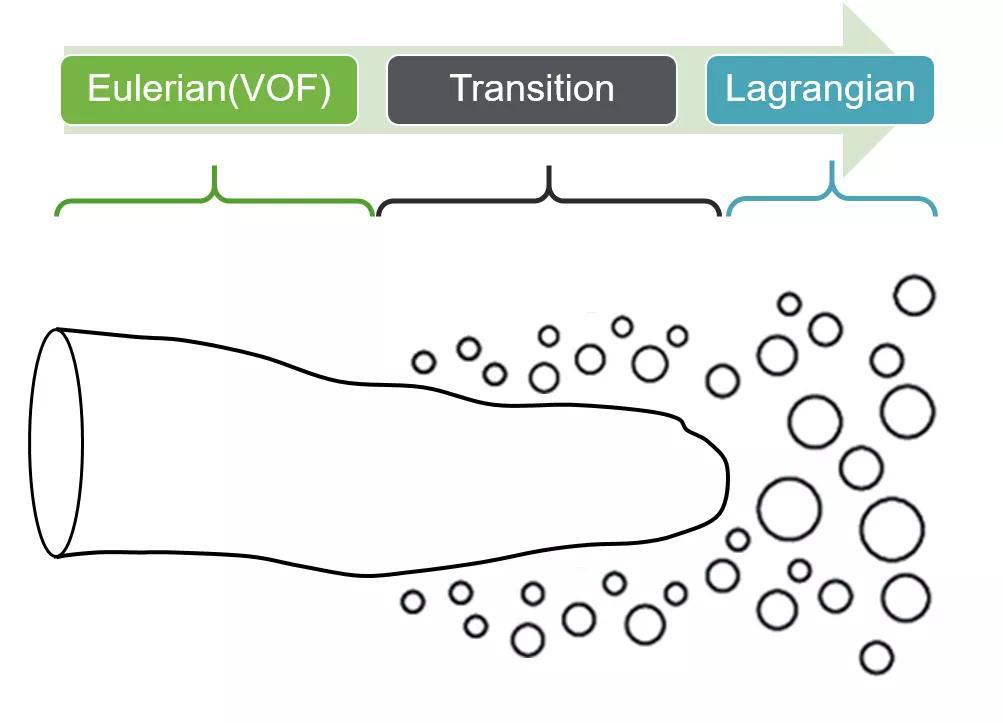
案例1 :液体射流的雾化
这是对垂直向上气流喷射的液体射流的分析。
射流表面变得不稳定,分裂成小的液滴。
分裂的小液滴带被转化成随气流流动的颗粒。
可以通过转换为粒子,可以减少网格,高精度计算破碎。
案例2 :轮胎溅水
这是一个分析计算水飞溅时,汽车轮胎进入水坑。
由于产生细液滴,因此可以通过将液滴转化为颗粒来执行有效的计算。
10 动态接触角
What:
当液滴移动或润湿和扩散时,其接触角会动态变化。
通过考虑接触角的动态变化,改善了液滴行为的再现性。
Benefits:
提高接触角精度
Where:
使用[Condition Wizard]–[Free surface]-[surface tension]设置。
Target:
由于液体的湿扩散,接触角动态变化的问题。
𝐶𝑎 数字应为1或更少.
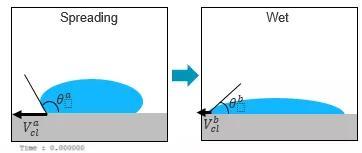
案例:液滴扩散
比较计算液滴在壁面上的扩散时为0。
当静态接触角恒定时,略微扩张。
当考虑动态接触角时,与实验结果吻合较好。
11 空化模型-Schnerr-Sauer model
What:
该空化模型基于均匀模型,该模型假设汽相和液相局部且均匀分布。
假设每单位液体体积的气泡数是恒定的。
气泡半径是一个输入参数。
它不同于全空化模型,因为它不使用湍流能量来计算蒸发和冷凝。
Benefits:
由于该模型不使用湍流能量,因此可与任何湍流模型或LES结合使用。
Where:
在条件向导的[Avitation]-[Detail Settings]中,从[Avitation model]中选择[Schnerr Sauer model]。
Target:
螺旋桨空化的LES/DES分析。
案例:空化模型比较案例
空化模型比较案例.wmv
scFLOW V2022中三种空化模型的结果比较
定性上与实验数据吻合良好。
三种空化模型在数量上有很好的一致性.
12 DEM功能增强
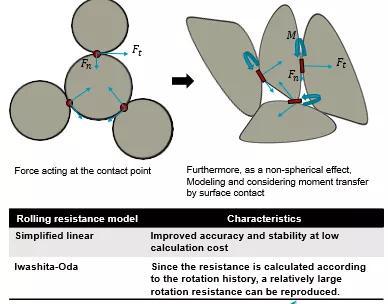
滚动摩擦阻力模型的改进-对应非球状模型
简化线性模型和Iwashita Oda模型已作为新的滚动阻力模型.
简化线性模型和Iwashita Oda模型已作为新的滚动阻力模型实施。
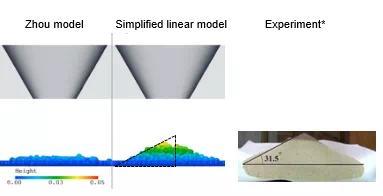
案例1:休止角模拟
当一定数量的颗粒落下并堆积时,颗粒形成的坡度角称为休止角。
作为确定粒子特性的数值实验,休止角的验证是一个常用的课题。
由于旋转运动的处理对于将休止角与实验相匹配非常重要,因此有必要正确选择滚动阻力模型。
在右边的示例中,可以使用简化的线性模型再现实验结果。
案例2:贯入试验仿真案例
在容器中散布颗粒以产生颗粒床。 将圆柱形杆推入颗粒床。
测量作用在杆底部的反作用力。
该贯入试验是测量土壤力学性质的一般试验。
在右侧的示例中,通过指定屈服强度来捕获纸张*的参考值的趋势。
案例3:巴西坚果仿真
圆柱形容器中有两种不同粒径的颗粒。
振动容器使其混合。
振动使两种颗粒混合,混合指数逐渐增大。
由于渗滤现象,大颗粒被提起并发生偏析,最终降低混合指数。
这样,混合指数被输出,以评估由于偏析导致颗粒混合不均匀的情况。
其他案例:
泥石流防护网
非球形颗粒混合
13 非牛顿流体
广义牛顿流体(GNF)模型可用于设定不可压缩流体的粘度。
仿真对象:
非牛顿流体,如油漆、浆糊、血液、钻井液、食品、药品等。
剪切速率相关粘度模型:
Constant (Newtonian)
Power law model
Sisko model
Cross model
Carreau-Yasuda model
Powel-Eyring model
Herschel-Bulkley model
Casson model
温度相关的粘度模型:
Arrhenius law model
Exponential law model
Williams-Landel-Ferry (WLF) model
案例1:分配器
使用分配器注入四种液体:
水(左上角)、虚拟高粘度流体(右上角)
黄原胶溶液(左下)、淀粉在水中的悬浮液(右下)
案例2:立方体坠落仿真
分析概述:将铁立方体坠落到四种液体中:
水(左上角)
虚拟高粘度流体(右上角)
黄原胶溶液(左下)
淀粉在水中的悬浮液(右下)
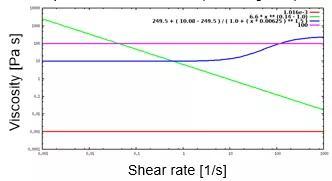

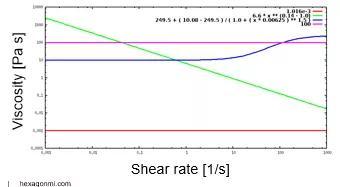
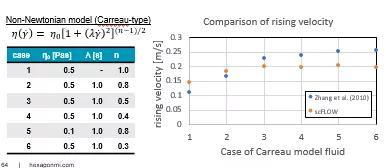
案例3:剪切变稀流体中气泡的上升
这是一个1厘米大小的气泡在剪切变稀流体中上升的分析。
就粘度分布和气泡的终端速度而言,scFLOW结果与Zhang等人(2010)的先前工作具有较好的一致性。


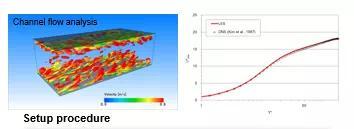
14 LES计算
What:
将动态Smagorinsky模型引入LES中的SGS模型。该SGS模型解决了Smagorinsky模型中的问题,
例如Smagorinsky模型常数无法唯一确定,以及涡流粘度的近壁极限行为无法 正确再现。
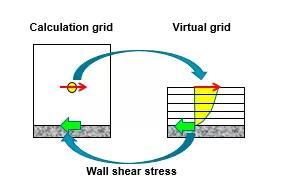
引入壁面边界条件,即Kawai-Larsson的壁面模型*1,以减少网格数量,实现低成本大涡模拟。
Benefits:
与WALE模型一样,可以预期LES计算比Smagorinsky模型更精确.
Where:
在条件向导的[Analysis Type]中的[Method of Flow Analysis]对话框中,为[湍流模型]选择[LES],并为SGS模型选择[Dynamic Smagorinsky Model].
Target:
无法唯一确定Smagorinsky模型常数或壁面湍流非常重要的分析