乐音感知系列(二)谐波与音程
Hi,各位有心与ACOUTEC一起成长的宝宝们。
上一期我们介绍了乐音的基频与谐波。在此基础上,本期讲一讲谐波之间的音程关系。

从声学角度来说,一个能被感知音高的声音都是由称为谐波的、基频的整数倍的频率成分组成,每个谐波都是一个正弦波。由于听觉系统是根据频率成分分析声音的(可参考ACOUTEC发表的声音与听觉系列知识第一期介绍的人耳结构相关的知识点),因此,这些谐波对理解周期性声波的分析与合成是非常重要的,而且研究各个谐波之间的音乐关系,是西方音乐和声发展的核心内容。
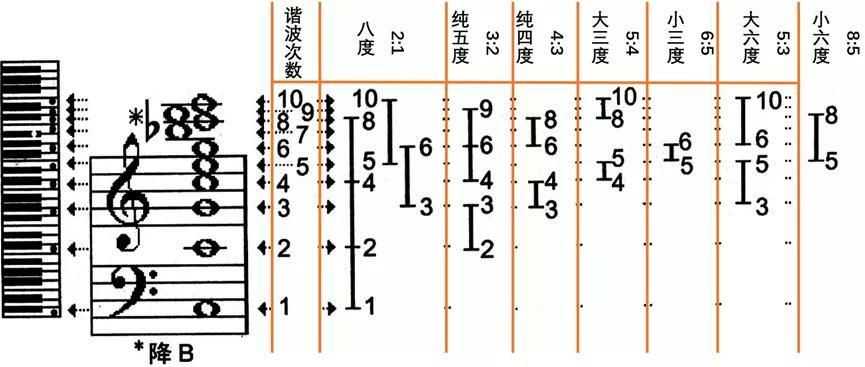
音符C3的第1次到第10次谐波的频率比和音程关系,以及在键盘和五线谱上的位置如上图所示。现代键盘上的音程关系(除倍频程外)只是近似于上述的音程关系,这与所使用的调律系统有关。
在一系列自然谐波中,相邻谐波的音程开始于基频,用五线谱和键盘上的琴键表示出来,依次是八度(2:1)、纯五度(3:2)、纯四度(4:3)、大三度(5:4)、小三度(6:5)、减三度(7:6)、增二度(8:7)、大全音(9:8)和小全音(10:9)。上图只表示出其中部分音程。
非临近谐波之间的音程频率比也可以从图中得出。例如,第4次谐波与基频之间的音程是两个倍频程,频率比是4:1,相当于两次加倍的关系。同理,三个倍频程的频率比是8:1,一个倍频程加上一个五度的频率比是3:1。

两个或更多互相邻接的音程是可以相加或者相减的,相加相减后形成新的音程。如:大二度加大二度成为大三度音程;大二度加小三度成为纯四度音程。八度减纯五度成为纯四度音程;八度减纯五度,再减去小三度成为大二度音程。
问题是音程做运算时,其对应的频率比将如何计算?
正确的计算方法是:将两个相加的音程的频率比相乘,所得出的即为新音程的频率比;同理,将两个相减的音程的频率比相除,所得即为新音程的频率比。
大三度的频率比为5/4;小六度的频率比为8/5。这两个音程相加,应该是八度,而我们已知八度音程的频率比是2/1。用这三个音程举例验证上述音程计算方法如下。
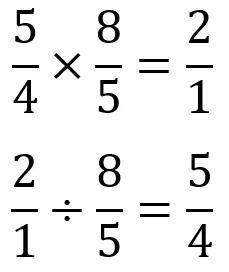

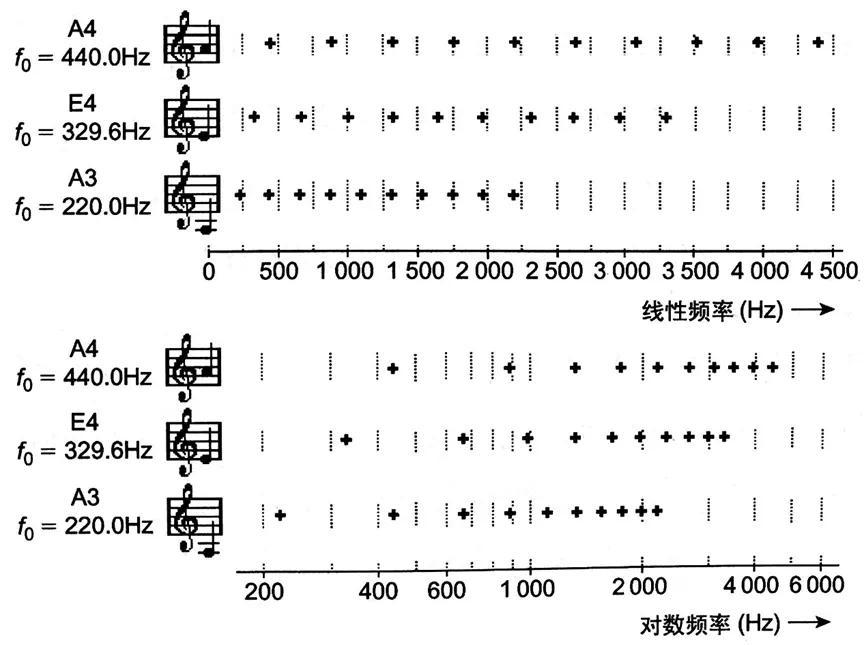
上图表示A3(f0=220Hz)、E4(f0=329.6Hz)、A4(f0=440Hz)的前10个谐波频率分别在线性坐标轴和对数坐标轴上的位置。谐波之间的间隔在线性坐标轴上是相等的,而在对数坐标轴上间距会随着频率的增大变得越来越小。尽管看上去对数坐标轴上谐波的分布比线性坐标轴复杂,但是对于基频不同的音符,例如E4和A4,其谐波分布形式在对数坐标轴上是一致的,但在线性坐标轴上却不相同。
上述特性和音色感知有很大关系。由于听觉系统的基底膜部位和对数频率的分布相一致,对数频率坐标最能代表听觉系统对固定音高乐器音符的各谐波成分的感觉加权特性。

在听觉感知的研究中使用对数频率坐标的好处在于,在分析频率比相同的频率分量时,听觉系统可以给出相同的感觉权重。上图为一些常用的音程标注在对数频率轴上,一直延伸到听觉的上限频率。
值得注意的是,在对数坐标上相同音程之间的间距是相等的。
如果在对数频率轴上,把任意一个音符加倍(或者减半),那么在听觉上就相当于把这个音程提升(或降低)了一个八度,乘以3/2(或除以3/2)在听觉上相当于把这个音程提升(或降低)了一个纯五度,以此类推。
我们感知到的所有音程关系(八度、纯五度、纯四度、大三度等),不管出现在哪个频率范围,都会很相似。例如,两个音符构成的大六度,不管是用两个低音提琴演奏,还是用两只长笛吹奏,他们在音程上所带来的感觉是相似的。以这种方式,听觉频率分析机理的对数本质为我们理解音程和音高的主观感觉奠定了基础。

本期讲解了谐波与音程的关系,为下一期介绍音高的主观感知做了铺垫。




