Fluent指南｜01 空间离散方法

本文摘要（由AI生成）：

本文介绍了在复杂求解设置中，高阶项松弛作为一种有效策略，可以最小化求解过程中的交互，并从一阶格式开始求解后切换到二阶空间离散。高阶项松弛选项在Solution Methods任务页中启用，用户可选择对所有变量或仅对流动变量进行松弛，并设置适当的松弛因子。此外，还详述了如何为标量方程、压力、密度、体积分数和组分输运选择不同的空间离散化方法，并强调了在某些情况下（如启用Non-Iterative Time Advancement选项或采用基于压力的耦合算法时）高阶项松弛的限制和注意事项。

本文描述Fluent中空间离散格式的选取方法。

注：本文内容译自Fluent UserGuide 32.2，留待后期查阅。

”

1 Gradient计算

梯度不仅用于构造网格面上的标量值，而且还用于计算二次扩散项和速度导数。

Fluent中包括三种梯度计算方法：

• Green-Gauss Cell Based
• Green-Gauss Node Based
• Least Squares Cell Based

梯度算法可以在Solution > Methods 面板中的Gradient下拉列表中进行选择。

此外，Fluent还允许为每个控制方程的对流项选择离散格式(粘性项自动使用二阶精度)。默认情况下，使用压力基求解器或密度基求解器求解单相流问题时，对于流动方程和所有标量方程(湍流除外)的对流项使用二阶迎风格式（Second Order Upwind），湍流物理量相关方程则使用一阶迎风格式（First Order Upwind）进行离散求解。对于多相流问题，流动方程默认使用一阶迎风离散化。

当使用压力基求解器时，可以指定压力插值算法。

2 一阶精度 vs. 二阶精度

当流动方向与网格方向一致时(如用四边形或六面体网格模拟的矩形管道中的层流流动)，一阶迎风离散格式的计算精度是可以接受的。然而当流动与网格方向不一致时(即当流动斜穿过网格线时)，对流项的一阶离散会增加数值离散误差(出现数值扩散)。对于三角形和四面体网格，由于流动无法与网格对齐，因此通常使用二阶离散方法。对于四边形/六面体网格，使用二阶离散也可以获得更好的结果，特别是对于复杂的流动问题。

总而言之，虽然一阶格式通常比二阶格式有更好的收敛性，但它常常会产生不太精确的结果，特别是在使用三角形/四面体网格时表现更糟。

多数情况下，可以直接使用二阶格式进行计算。但是在一些情况下，可能需要先从一阶格式开始计算，然后在进行几次迭代之后切换到二阶格式继续进行计算。例如，如果运行的是高马赫数流动计算，其初始值与最终解可能存在较大差异，此时通常需要使用一阶格式执行少数几次迭代，然后打开二阶格式继续计算直至计算收敛。这种情况也可以先采用完全多重网格初始化（FMG初始化），然后从一开始就使用二阶格式进行计算。

对于与网格对齐的简单流动(例如，使用四边形或六面体网格建模的矩形管道中的层流流动)问题，数值扩散较轻，可以使用一阶格式而不会有任何明显的精度损失。

如果使用二阶格式时遇到收敛困难，此时可以尝试使用一阶格式进行计算。

虽然高阶格式可以获得更高的精度，但在某些流动条件下也可能导致收敛困难和计算不稳定。另一方面，使用一阶格式可能无法提供所需的精度。在保持良好稳定性的同时提高精度的一种方法是使用离散混合因子。此功能可用于密度基和压力基求解器，其通过TUI命令进行启用：

solve → set → numerics

当TUI窗口出现以下提示时，输入一个0~1之间的值即可。

1st-order to higher-order blending factor [min=0.0 - max=1.0]

混合因子为0时梯度计算将采用一阶离散格式，而设置为1表示恢复为高阶离散格式。混合因子小于1(通常为0.75或0.5)将使对流通量更具扩散性，此时可能在一些流动条件下无法完全使用高阶格式时得到稳定的计算结果。

注意：为了使用此功能，需确保在Solution Methods任务页面中为所需的变量选择了允许的高阶格式。

”

3 其他离散格式

对于存在旋转或涡旋的流动问题，使用QUICK或三阶MUSCL离散格式能够获取比二阶格式更高的计算精度。QUICK格式通常适用于四边形及六面体网格，而MUSCL格式则适用于所有类型的计算网格。然而，总体来说二阶格式的精度是足够的，QUICK格式并不会在精度上有显著的提高。

注：如果在混合网格中使用QUICK格式，则仅有四边形和六面体网格能使用QUICK格式，其他类型的计算网格将会使用二阶迎风格式。

”

当使用LES、DES、SAS、SBES和SDES等湍流模型时，可以使用有界中心差分及中心差分格式，并且中心差分格式应该仅在网格间距足够细以确保局部Peclet数小于1时使用。Peclet数定义为：

式中，为流体密度；为局部网格内的流体速度；为长度尺度（如网格尺寸）；为流体的扩散系数。

4 选择压力插值格式

当在Fluent中使用基于压力的求解器时，可以选用许多类型的压力插值格式。虽然对于大多数单相流问题，可以选择使用二阶格式。但在一些特殊的模型中选择其他的插值格式可能更加合适。

• 对于高旋度、高瑞利数、高速旋转流及强曲率弯曲区域的流动，推荐使用PRESTO!格式
• 对于欧拉多相模型，默认采用PRESTO！格式。然而对于使用非迭代求解器的多流体VOF问题，二阶插值格在具有歪斜网格的模型中表现更稳健，而Body Force Weighted插值格式对于具有大的体积和倾斜网格的情况更稳健
• 对于VOF及Mixture多相流模型，应该使用PRESTO!或Modified Body Force Weighted插值格式
• PRESTO！格式比其他格式更全面
• 对于大多数问题来说，Modified Body Force Weighted格式是PRESTO!及Body Force Weighted格式的一个很好的替代。与PRESTO!格式相比，其对网格和时间步长的敏感度较低

Modified Body Force Weighted格式建议用于：

• 非迭代求解器(因为它提供了更好的健壮性)
• 计算域中存在大的体积力

该格式可用于Body Force Weighted格式受限的高粘性和旋转流动。

5 选择密度插值格式

当采用压力基求解器计算单相可压缩流动时，有4种密度插值格式可以选用。

• 默认的二阶迎风格式（second-order upwind）为压力修正方程的离散化提供了合理的稳定性，对大多数类型的流动都能够有较好的结果

• 一阶迎风格式（first-order upwind）具有较大的稳定性，但可能会平滑可压缩流动中的激波。如果要计算有激波的可压缩流动，则应使用二阶迎风格式或QUICK格式。

• 当使用四边形、六面体或混合网格时，强烈建议对包括密度在内的所有变量使用QUICK格式来处理含激波的可压缩流动

• 三阶MUSCL格式适用于任意网格，并且有可能通过减少数值扩散来提高所有类型网格的空间精度

注意：对于多相流，可压缩相利用选定的密度格式，不可压缩相利用算术平均。

”

6 高阶项松弛

高阶项松弛（High Order Term Relaxation, HOTR）的目的是提高高阶（高于一阶）空间离散时流动模拟的启动和通用求解性能。在某些情况下，该功能还可以防止收敛停滞。高阶项在某些情况下可能非常重要，并导致数值不稳定性，在激进的求解设置中尤其如此。在这种情况下，高阶项松弛是一种有用的策略，可以最大限度地减少求解过程中的交互。这是一种有效的替代方法，可以从一阶格式开始求解，然后在稍后阶段切换到二阶空间离散。

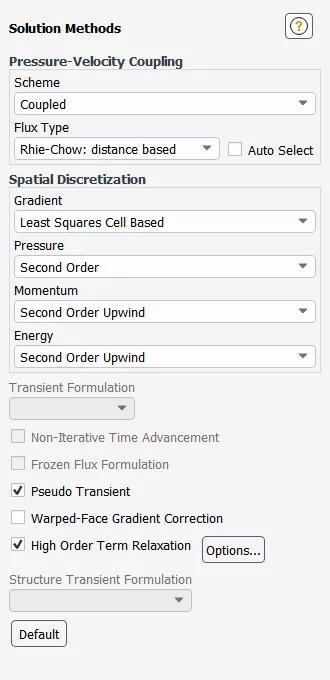
高阶项松弛选项可以从Solution Methods任务页启用，如下图所示。

点击按钮Options… 后，可以在Relaxation Options 对话框中进行必要的选择和设置，以进一步控制高阶项松弛。

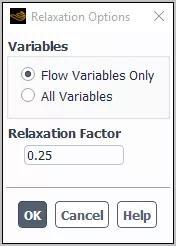
可以选择要松弛的All Variables，而不是仅选择默认的Flow Variables Only。

• 当选择选项Flow Variables Only 时，以下变量将会实施亚松弛：
• 速度分量
• 压力
• 能量
• 密度
• 湍流量（雷诺应力除外）
• 体积分数
• 如果选择All Varaiables ，则对每个用高阶格式离散的变量进行松弛

对于稳态情况，松弛因子的默认值为0.25，对于瞬态情况，松弛因子的默认值为0.75。相同的因子应用于所有求解的方程。

使用高阶项松弛选项时存在以下限制：

• 启用Non-Iterative Time Advancement选项时，高阶项松弛选项不可用，因为模拟达不到所需的高阶空间精度水平
• 一般来说，高阶项松弛适用于瞬态流动。不过使用时应小心。要在每个时间步收敛时获得高阶精度，必须增加每个时间步的迭代次数，以确保满足原始收敛条件
• 当为特定的输运方程选择QUICK格式时，该方程不适用欠松弛

7 用户输入

通过模型树节点Solution → Methods可以打开设置离散算法选择面板。

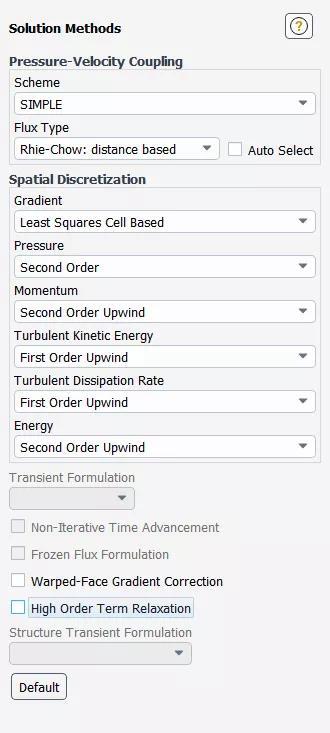
对于Spatial Discretization下列出的每个标量方程（动量、能量、湍动能等），可以选择First Order Upwind、Second Order Upwind、QUICK、Third-Order MUSCL，或者（对于使用LES、DES、SAS、SDES或SBES湍流模型时的动量）下拉列表中的 Bounded Central Differencing（默认值）或相邻的Central Differencing。

如果使用的是压力基求解器，请在Pressure旁边的下拉列表中选择Spatial Discretization下的压力插值格式。可以选择Standard、 PRESTO!、Linear、Second Order、Body Force Weighted、 Modified Body Force Weighted。

注意：PRESTO!格式的低阶格式可以通过限制其高阶项来使用，通过使用文本命令/solve/set/numerics可以实现此功能。当询问limit high-order terms for PRESTO! pressure scheme?时输入yes即可。当采用基于压力的耦合算法时，当原始的PRESTO!算法要么无法收敛，要么在压力场中产生非物理振荡时，使用此修正可以用来稳定求解过程。

”

如果使用的是压力基求解器并且流动介质是可压缩的（即使用的是理想气体定律），请在Density旁边的Spatial Discretization下拉列表中选择密度插值格式。此时可以选择 First Order Upwind、 Second Order Upwind、QUICK 或Third-Order MUSCLL。（注意，对于不可压缩流动，不会出现Density选项）

如果在使用压力基求解器时启用 VOF 模型，则可用的体积分数插值格式有Geo-Reconstruct、CICSAM、Modified HRIC、Compressive 和 QUICK。

如果模型中涉及组分输运，可以将单个组分的算法设置为First Order Upwind、 Second Order Upwind、QUICK或 Third-Order MUSCL。但是，如果希望所有组分都使用相同的离散化方案，那么与其单独设置每个组分，只需启用Set All Species Discretizations Together选项即可。

如果更改了空间离散化的设置，但随后又想返回到Fluent 的默认设置，可以单击Default按钮。

重要：如果壁面附近的网格拓扑存在阶梯式的棱柱网格，不要在MUSCLE中使用基于节点的梯度方法。

”