深入剖析三维几何内核(5)--布尔运算
本文摘要(由AI生成):
本文深入剖析了三维几何内核中的基础数据结构,特别是其拓扑结构在物体编辑修改后的重要性。文章介绍了基本的布尔运算,并指出在实际应用中会遇到更复杂的情况,如非二维流形的处理、高阶曲面求交精度问题等。此外,文章还讨论了布尔运算的一些高级功能,如Chop运算、不同维度对象的布尔运算等,并提及了OCC几何内核在布尔运算方面的进展。总体而言,本文为理解三维几何内核中的布尔运算提供了全面的视角。
布尔运算是三维几何内核的一个基本功能,其功能,稳定性,性能直接反应了内核的质量。
本文分三个部分来讲:
1.布尔运算的基本原理和算法
2.布尔运算里的一些高级功能
3.OCC的布尔运算功能
1.布尔运算的基本原理和算法
常见的三种布尔运算:并集,交集,减集。其实这三种布尔运算的前面运算逻辑是一样的,最后一步不同。
1.并集就是把两个物体合并成一个物体
2.交集是求两个物体公共的部分
3.减集是从一个物体中减去两个物体公共的部分
为了简化描述,我们只讨论实体Solid和实体Solid的布尔运算,其它类型几何之间的计算类似(比如面Face和实体Solid,面Face和面Face)。
在深入剖析三维几何内核(4)--曲面的艺术一文中,我们知道基于B-Rep的三维结构都是由面Face构成,所以三维实体的布尔运算也是基于面Face的几何信息,相比单纯的面Face和面Face之间的布尔运算,三维实体Solid布尔运算多出的一步是需要维护Face拓扑之上的SHELL和BODY等拓扑信息,而几何信息则是完全相同的。
布尔运算基础算法涉及到的计算有:
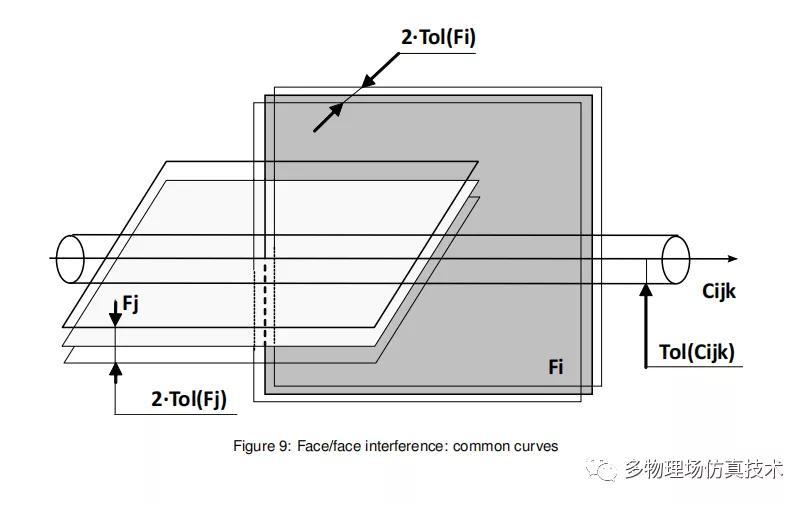
1.几何面的相交计算,需要得出交点,交线等几何信息;
2.基于原始拓扑结构,对Face面进行裁剪;
3.裁剪区域Edge边和顶点Vertex的拓扑重建。
整个计算流程如下:
1.判断两个实体是否有重合。为了加快计算效率,可以首先使用包围盒进行过滤,即包围盒如果不相交,则两实体一定不会相交;还可以判断一个实体的点是否在另外一个实体里,如果在那两实体一定相交,这些加速算法可以在任一拓扑层级进行,后续再做详细介绍。
2.假设已经确定两个实体相交,遍历一个实体的面,计算每个面和另外一个实体的面的相交情况。面面相交通常是一条线Curve
3.将所有相交的线Curve分别加到原来的两个实体Solid上
4.根据实际操作需求(并,交,减),对两个对象进行裁剪以及重新生成新的拓扑结构。
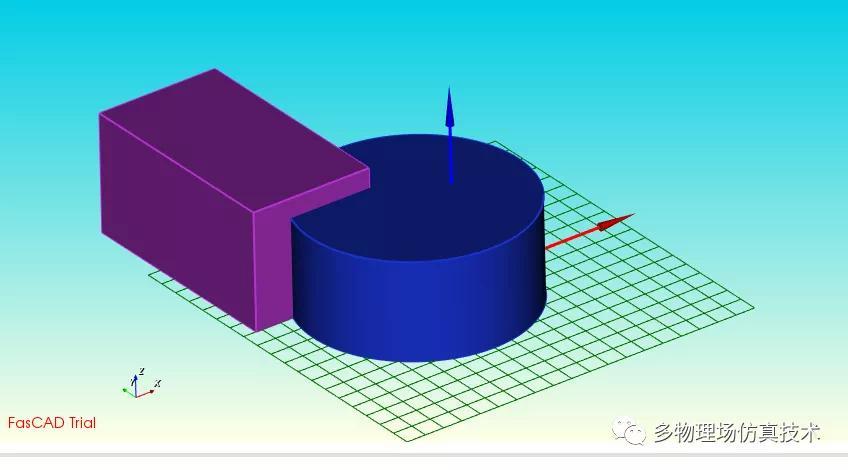
以两个长方体布尔并运算为例说明
布尔运算一般是两个物体,按照顺序习惯将第二个物体叫Tool,也就是加工工具的意思,第一个对象OCC里叫Object,PS里叫Target,ACIS里叫Blank。
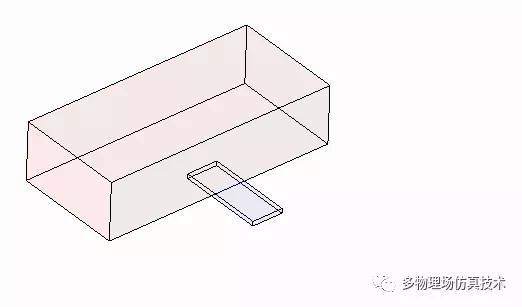
初始两个相交的立方体A和B
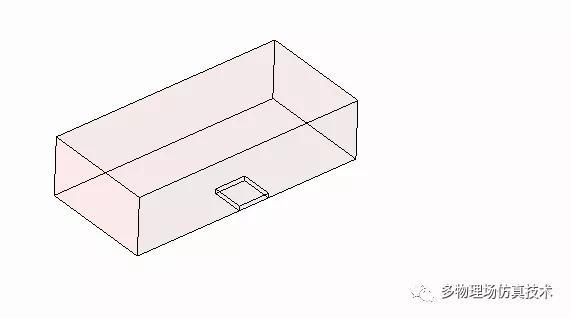
计算出所有相交面的边,将拓扑边和几何信息加到物体A上
计算出所有相交面的边,将拓扑边和几何信息加到物体B上
交集:只需要把计算出的公共部分进行拓扑重建即可
并集:将公共部分的拓扑和几何去掉,保留A和B,拓扑重建
减集:将对应的原始部分去掉公共部分即可,拓扑重建
在这个过程中,反复提到了拓扑重建。我们在深入剖析三维几何内核(3)--基础数据结构中建立了基本的拓扑结构,其目的之一就是在对物体进行编辑修改后,还能用基本的拓扑结构来表达三维物体。布尔运算之后同样也要遵守初始的拓扑规则定义,比如我们建立的面的方向,Loop的方向,Edge的方向等,仍然要保持一致。
这里只是介绍了基本的布尔运算,实际中会有更多需要处理的复杂情况:
1. 非二维流形的处理
2. 高阶曲面的求交精度问题
3. 不同维度几何求交,线面求交,线体求交
4. 复杂几何拓扑重建
5. 求交性能问题
6. 布尔运算顺序
2.布尔运算里的一些高级功能
在基本运算的基础上,根据实际需求,衍生出很多相关运算。
1.Chop运算:
Chop,顾名思义就是削除。它是布尔交和布尔减得合集。
2.不同维度对象的布尔运算:
前面介绍的是实体Solid和Solid的运算,在实际中有大量的面Face和实体Solid,Edge边和面Face,Edge边和实体Solid的计算。底层计算本质上也是一样的,只是拓扑重建步骤不同。
3.Imprint运算:
压印,通常我们需要把线或者面放(印)到另外一个对象上。
4.Cell结构:
Cell结构在B-Rep结构提出之后不久就被提出来。Cell结构对应于实体Solid,主要用来保留,编辑,追溯Solid实体的属性信息。
5.Split运算:
Split分割操作可以将一个实体Solid分成两个或多个实体。本质上也是一个实体Solid和面Face的布尔运算
6.Glue运算
在某些情况下,我们知道两个对象的一些特征,比如两个大的模型,都只在某个面上有重合,可以采用Glue粘贴操作,也就是指定Glue的拓扑,只在特定位置进行布尔计算,这样可以大大提高操作效率。Sew也是同样的道理。
7.Fuzzy布尔运算
也就是模糊布尔运算,在某些场合通过设置一定的容差和参数,可以稳定的处理模型接触地方近似一致,轻微干涉,不对齐的情况
8.性能提升
布尔运算是一种非常耗时的运算,所以在针对大规模和特定场景时,需要用一定的加速算法来提升性能。
在机械加工中,要在某个复杂的对象A上钻100个孔,这是一个典型的布尔减运算。通常做法是创建孔的几何,然后再一个一个的执行布尔减运算。由布尔运算算法得知,每次运算都需要遍历几何的面进行面面相交计算。如果我们先将孔进行并运算得到B,然后再用A布尔减B,虽然面面相交计算次数没有减少,但是相应的各种过滤和无用算法调用次数会减少很多,能显著提升计算性能。
3.OCC的布尔运算功能
ACIS和PARASOLID里提供了大量的基础布尔运算和相关扩展功能,其中许多来自于实际应用需求,比如ACIS中有针对符复合材料,流体,多物理场的非二维流体的布尔运算,PARASOLID里的实体抽中面,Blend运算等。
笔者多年使用PARASOLID,ACIS和OCC,考虑到前两者都是商业内核,就不展开描述了。
需要说明的是PARASOLID,ACIS,OCC都是通用三维几何内核,在布尔运算方面也都是中规中矩的运算,针对很多实际业务时性能并不一定最优,还有很大的改进余地。之前见过一些做几何内核公司,拿特定的布尔运算和测试用例做性能比较,得出PARASOLID和ACIS布尔运算性能较差的结论,其实意义不大。不过这也说明如果能开发专业而非通用的几何内核,在业务上可以大幅提升性能。
稍微介绍下OCC里的布尔运算:
经过多年的发展,相对于早期的版本,OCC在布尔运算上可以说是有了质的飞跃。以7.3版本为例,实际应用中,包含两个对象的100M以下的STEP文件导入后,布尔运算可以稳定的实现,虽然相比ACIS和PARASOLID性能方面还有不少差距。
在OCC的文档中,有一篇文档
occt_boolean_operations.pdf是专门介绍布尔运算的,文档不仅介绍了相关API的用法,而且详细列举出了各种布尔运算的应用场景,覆盖了实际应用中的大部分情况。