Abaqus|基于智能优化算法的薄壁结构加强筋位置反演
本文你将获得如下干货:
1. 有限元模型修正法FEMU结合智能优化算法反演了加强筋位置布局的源程序(python程序,可反演位置、厚度、材料参数,通用反演程序)
2. 参数化建模的一些技巧;
3. 直接搜索法和智能算法两种反演方法,以及了解他们的优势所在;
1.导读
薄壁结构最常见的失效方式是屈曲(失稳)。为了避免此类结构发生屈曲现象,可以使用加强筋,加强筋可增加结合面的强度。屈曲临界载荷是衡量结构发生屈曲现象的最小载荷,由下式决定:
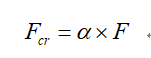
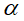 为屈曲载荷因子,F为外载荷。由上式可知,在外载一定的时候,临街载荷与屈曲载荷因子成正比,而屈曲载荷因子与加强筋的位置有关。因此为了提高结构的稳定性,需要找到加强筋的最优位置使得该结构拥有最大屈曲载荷因子。
为屈曲载荷因子,F为外载荷。由上式可知,在外载一定的时候,临街载荷与屈曲载荷因子成正比,而屈曲载荷因子与加强筋的位置有关。因此为了提高结构的稳定性,需要找到加强筋的最优位置使得该结构拥有最大屈曲载荷因子。
寻找最优位置的问题是一个反问题,可通过优化算法来获到最优解。差分进化算法是一种全局智能优化算法,是遗传算法的变体,可高效获得最优解。本文使用智能优化算法对位置参数进行了反演并使用遍历搜索优化算法来进行了对比。
2.问题描述
针对图1优化前所示结构,优化轴向4个加强筋位置,使得屈曲载荷因子最大。圆筒高400mm,圆筒直径为400mm,薄壁厚1mm,加强筋厚2mm。圆筒在顶端受到大小为500N,方向为-y方向的集中力。
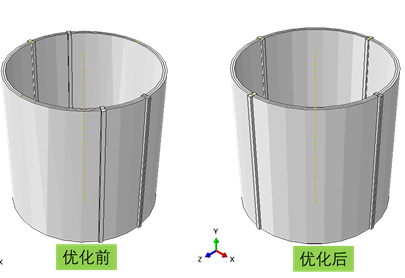
图1 带有加强筋的圆筒模型
通过智能差分进化算法获得的加强筋均匀分布在了圆筒的四周,很符合力学常识。
3. 代码详解
这一部分将结合代码详细展现如何实现这一过程的技术细节以及智能优化算法的优势。代码是通过Python脚本来实现,其代码主要包含三个模块runAbaqus、main_DE_inverse、main_TS_inverse,分别代表执行CAE计算、差分进化算法反演和遍历搜索算法反演。
runAbaqus(theta): 运行Abaqus进行CAE计算,输入为加强筋位置所在的角度,并在后处理提取出屈曲载荷因子。在进行参数优化时,建立参数化模型是最有挑战的一项任务。
内容简介:有限元模型修正法FEMU结合智能优化算法反演了加强筋位置布局的源程序(python程序,可反演位置、厚度、材料参数,通用反演程序)





