深入剖析三维几何内核(3)--基础数据结构
为了涵盖B-Rep结构
(Boundary-Representation)的基础操作,需要定义一些基本的数据结构。参考OCC的BREP结构定义,几何上至少需要定义:
Point
Curve
Surface
Point 包含基本的坐标X,Y,Z信息以及索引号。
Curve作为抽象几何定义,又可以衍生出各种形式的几何曲线,比如直线Line,圆弧Arc,椭圆弧Ellipse,样条曲线,NURBS,B样条等等。
考虑其中最简单的直线定义:
1.两端有端点的线段StraightLine;
只需定义两个端点索引即可,其它信息都可以根据端点信息算出;
2.只有一端有端点的射线Ray ;
需要定义一个端点,再给出射线的方向(方向为三维向量Vector,需要单独给出定义,包括三维向量的加减乘除,归一化等等操作)
3.两端都没有端点的无线延长线InfineLine
无限直线有多种定义方式,比如函数表达式,或者给定过直线一点以及方向等。
Surface的几何衍生类也类似。
拓扑自底向上至少需要定义:
1.Vertex
2.Edge
3.Loop
4.Face
5.Shell
6.Solid
在机械加工CAM,仿真CAE,CFD,EDA等领域,我们需要知道附加在某个三维实体的属性信息(Attribute/Property),最常见的就是材料信息(Material),这类信息在几何对象进行修改时,需要继续保持其属性,因此需要一定的Cell数据结构来进行操作。
其中Face的基本定义:
Face的数据结构中至少要包含如下信息:
包含的所有Loop信息;
如果存在Shell或者Solid,要能拿到Shell和Solid的信息;
引用的几何面所定义的几何信息;
能直接取到Face以下所有的拓扑信息,包含Edge,Vertex;
Face所定义的边界信息;
继承自拓扑基类的其它信息,比如ID,矩阵转换(Transform),局部坐标系(Axis)等信息
其中Vertex和Point,Curve和Edge,Surface和Face,拓扑和几何数据结构可以建立一定的对应关系。
定义拓扑信息的目的是将位置关系和几何关系进行关联,方便后续数据操作,比如查询,遍历,计算等。
下面在FasCAD中以一个简单的三维实体四面体的创建,描述基本的B-Rep结构自底向上的构造过程。
1. 建立点的信息
1. 首先创建四个点坐标
2. 开启3D捕捉和顶点捕捉,将点两两之间用直线相连
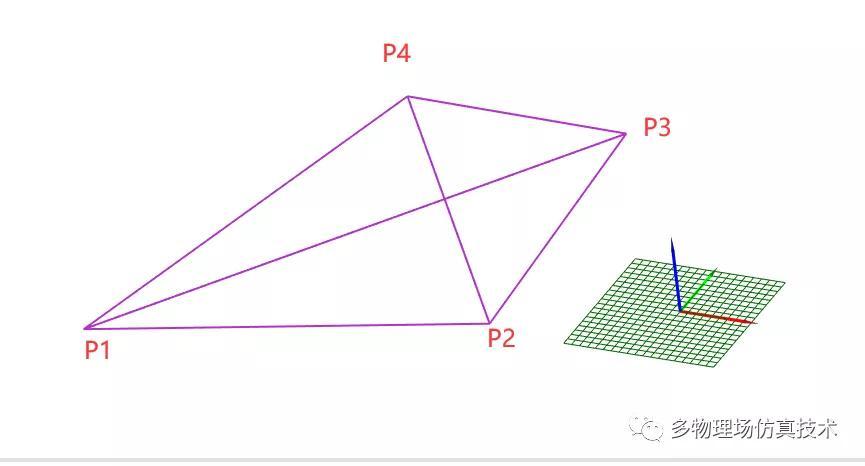
从视图上,我们已经可以表现出一个三维四面体实体结构了;但是这对于B-Rep结构还远远不够,我们需要将完整的拓扑结构建立出来。
2. 在点的基础上构建边Edge
由点的坐标可以构建成一条直线Line,Edge可以由两点构成,Line和Edge建立映射关系,需要注意的是所有的Edge是有方向的,即一个面上的所有边的方向首尾相接而成。
3. 建立环LOOP
所有的Edge可以构成一个环Loop,环最重要的特点是有方向性,可以作为内环和外环。比如一个面Face里有个孔Hole,Face的边界为外环(Outter Loop),孔的Loop为内环(Internal Loop),内环的方向通常和外环方向相反。
4. 建立面Face
三条Line构成一个封闭的平面三角形Surface,Surface和Face可以建立映射关系。一条Loop就可以构建面的拓扑结构了,同样,面也有方向,右手左手准则都可以,所有面的准则保持一致即可,四根手指的方向指向Loop的方向,大拇指方向即为面的方向。Face的方向除了对显示光照有用外,对使用有限元单元方法的刚度矩阵计算和组装也非常关键。
5. 建立实体Solid
有了面的信息后,就可以将所有的Face定义成一个Shell,然后将Shell封装成一个实体Solid。
这样我们就构建了一个完整的四面体B-Rep实体数据结构实例。
需要注意的是,非封闭的Shell无法构建成实体。比如一个长方体(Cuboid),在删除一个面后就不能构成实体了;从拓扑完整性上看,是不允许删除一个长方体的一个面;但有时候为了操作方便,有些前处理软件提供了Release功能,即允许删除长方体的一个面,在面删除后,实体自动退化成由五个面构成的Shell,在缺失的面补上后,又可以通过Shell生成实体Solid。
可见,如果使用B-Rep数据结构自底向上的方法创建三维实体是一件非常繁琐的事情。为了方便,一般会提供一些常用的基本实体的创建函数,比如长方体Cuboid,圆柱Cylinder,圆环Tours,圆台圆锥Cone,球Sphere等。
以上所定义的是基本的B-Rep数据结构,在这些数据结构的基础上,还可以根据实际需要或业务需求衍生或者减少数据结构定义。比如常见的实体Solid结构,如果存在大量Solid合并操作时,可以再派生出类似Assembly或者Compound实体结构。对于没有面组操作的实际业务,Shell可以拿掉。
综上所述,B-Rep数据结构是一种比较通用的三维数据结构,它能涵盖大部分三维设计工况;但也正是因为通用,数据结构尤其是拓扑设计比较庞大,在处理大模型时存在性能上的瓶颈。对于实际业务比较固定的情况,可以根据需要设计开发轻量级的三维几何数据结构。




