教你突破风机高精度性能验证和Optislang优化设计关键点
文章亮点
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺




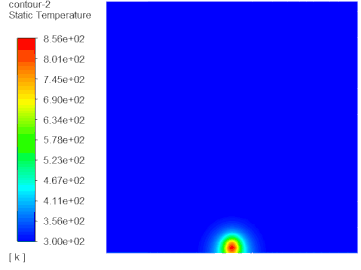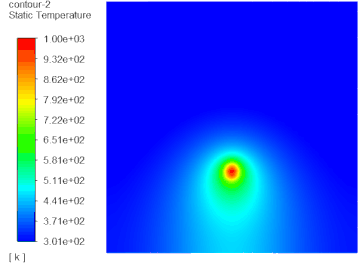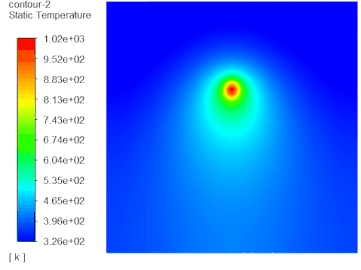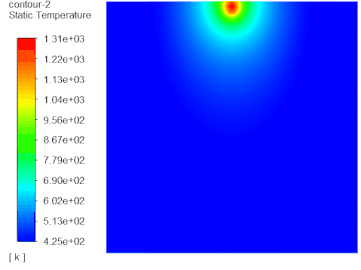
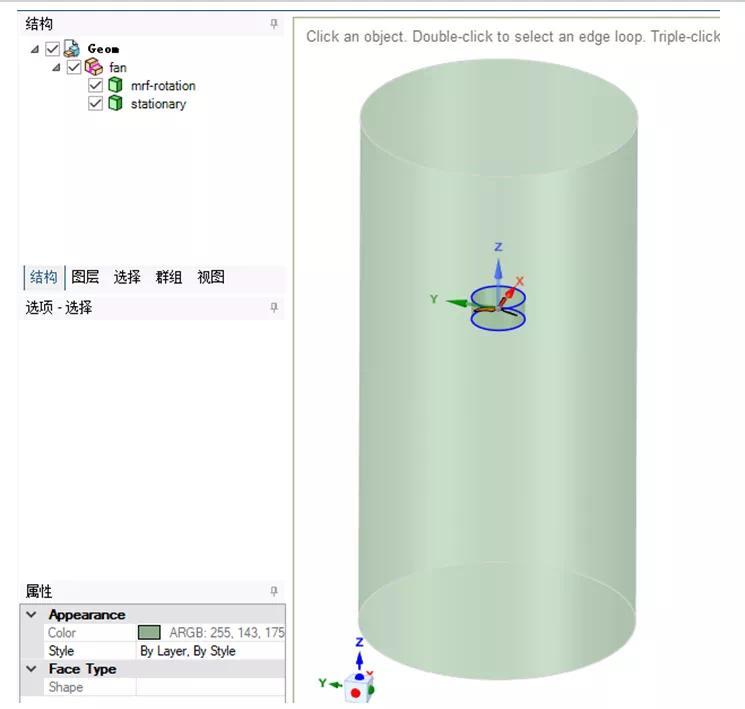
虽然MRF尺寸影响虽然很大,但是不能忽略求解域尺寸、湍流模型、y 、是否采用交界面形式、以及网格尺寸的影响;比如大家常用的采用动静interface配对的方法也会造成误差,这一点可通过动静区域共享拓扑的形式进行建模,这样就可以避免掉interface数据传递的误差,如下:
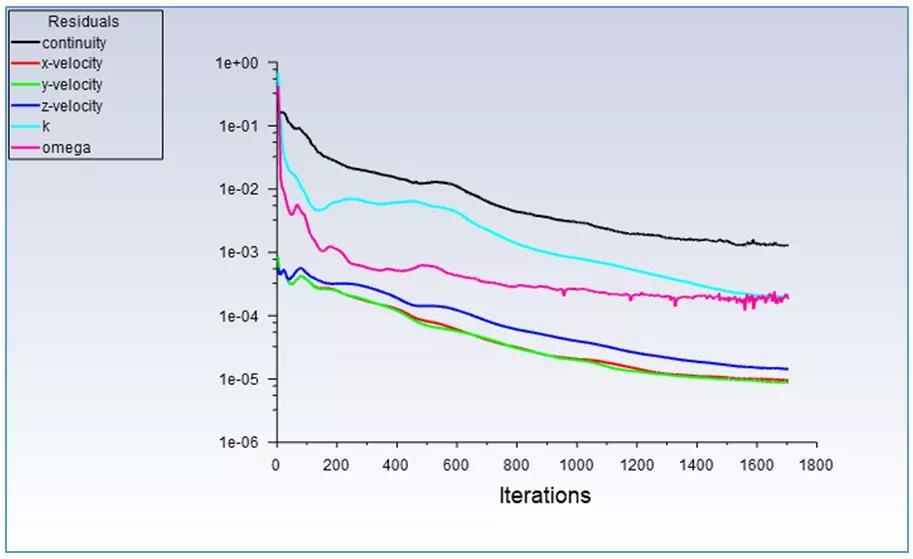
若没有足够的行业经验,通过优化风机外形,提高风机效率和风量是很难的事情,比如采用普通的四面体网格 一般优化软件(Designexploer),计算量很大,优化效率低;但是若采用纯六面体网格方案 新一代优化软件optislang,可做到在短时间内优化风机风量和效率;如下图使用TurboGrid meshing网格生成高质量纯六面体网格,并采用基于机器学习算法的optislang软件优化某风机的结果;在普通的个人工作站上只需要计算几天即可。


登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2022-01-06
最近编辑:4月前
作者推荐
还没有评论
相关推荐
最新文章