基于结构应力方法的焊接结构疲劳评估及实例分析(下篇)
本文摘要(由AI生成):
本文主要介绍了基于结构应力法的焊接结构疲劳寿命分析方法。首先介绍了焊接结构的重要性和疲劳破坏的特点,然后介绍了有限元模型的建立和结构应力的计算方法,最后通过实例分析了OSD钢桥焊趾疲劳破坏的疲劳寿命预测和抗疲劳优化设计。
一、写在文前
焊接技术作为现代制造业中的支柱技术之一,是制造强国的关键保障。由于其整体性强、轻量化、经济性好等优点,焊接结构被广泛应用于轨道交通、航空航天,船舶、重型装备等领域,安全承载问题也一直是业界关注的热点。然而焊接接头组织性能不均匀,应力集中大,存在残余应力、变形甚至焊接缺陷,这导致焊接接头往往是整体结构中最容易发生疲劳破坏的位置,据 资 料 统 计,在 焊 接 结 构 的 失 效 中,有70%-90%是由于焊接接头的疲劳断裂造成的[1]。因此,如何准确有效的对焊接结构进行疲劳分析,包括疲劳寿命预测与抗疲劳优化设计,是保证金属工程结构安全可靠运行的关键。基于结构应力方法的焊接结构疲劳评估及实例分析(上篇)对焊接结构疲劳的特殊性和国内外对焊接疲劳的研究现状进行了概述,并重点介绍了结构应力 Master S-N曲线方法(即美国工程师协会ASME标准方法)。本文(下篇)则以正交异性板钢桥结构为例,详细介绍结构应力方法分析焊接接头疲劳问题的具体步骤。分析采用ABAQUS有限元软件 Excel后处理进行。后续笔者将在仿真秀官网和App个人专栏-WeldMech上传视频教程,分别介绍利用二维和三维有限元模型 结构应力 主S-N曲线方法对OSD钢桥焊接接头进行疲劳分析的具体步骤,如有不当,欢迎各位同行和专家不吝赐教、批评指正,共同进步。二、原始试验数据
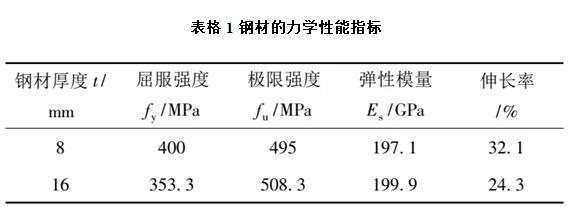
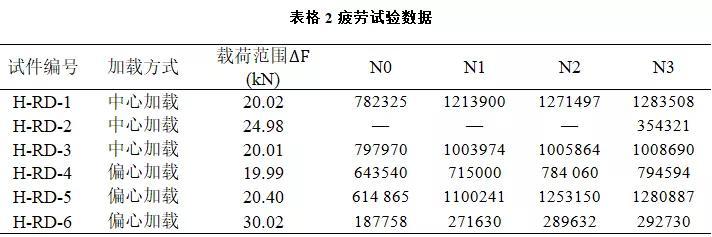
上海交通大学程斌教授课题组对组尺寸正交异性钢桥进行了详细的高周疲劳试验[2, 3],为研究OSD钢桥的疲劳行为提供了宝贵的试验数据。试验细节如下:节点试件共 6 个, 由 U 肋和盖板焊接而成。试件编号为 H-RD-1至H-RD-6,盖板长、宽、板厚分别为 1000, 400, 16 mm。纵肋为 U 肋,外侧开口为 300 mm, 宽为400 mm, 壁厚为 8 mm。圆 钢 中 心 距 离 盖 板 边 缘50 mm。焊接方式为二氧化碳气保焊, 焊缝为 8 mm,图 1 为试件构造和焊缝位置图。试件采用 Q345 钢,实测材料属性见表 1[3]。试验分为两种加载情况, 即试件H-RD-1,H-RD-2, H-RD-3 采用中心加载, 荷载中心与盖板中心重合; 试件 H-RD-4, H-RD-5, H-RD-6 采 用 偏 心 加 载, 荷 载 中 心 距 离 盖 板 边 缘350 mm ( 即位于 U 肋与盖板交线) 。具体如图 1[3]所示, 加载面积为 250 mm × 250 mm。疲劳荷载应力比 R = 0. 1, 加载频率为 3 ~ 4 Hz。
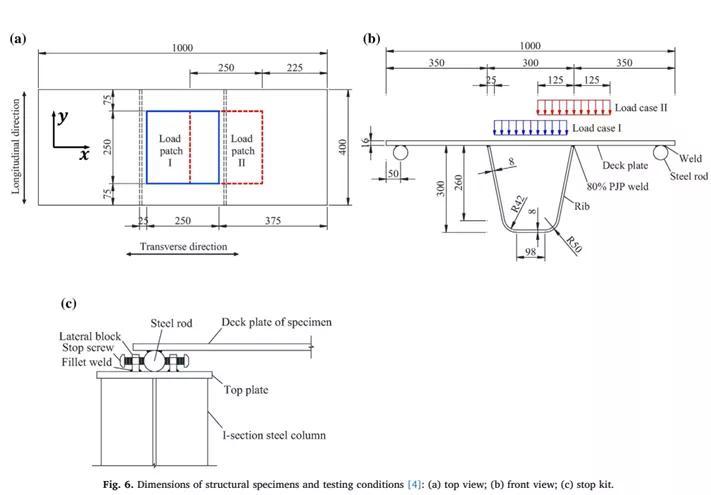
图 1 试件加载位置图 ( 单位: mm)
试件加载在 PMW400 - 500 疲劳试验机上进行,见图 2。为制作试件支座及分配荷载, 制作了 3组短柱。其中1组短柱用于将荷载均匀传递至盖板顶面, 并在短柱与试件之间放置 250 mm × 250 mm ×50 mm 的橡胶垫, 以模拟轮胎和桥面铺装的刚度。其余 2组短柱通过螺栓连接作为试件支座, 并在两边支座的上表面焊接定位钢片。将试件连同圆钢一并放入定位钢片间隙内后, 通过螺栓卡住一侧圆钢,这样不仅可以为试件提供纵向和横向约束, 而且圆钢可在间隙内自由转动, 从而成为理想的简支条件[3]。试验中疲劳裂纹长度通过人工标定测量, 裂纹深度通过相控阵超声测量仪测得。同时记录疲劳寿命 N0, N1, N2, N3, 其中 N0为裂纹萌生时荷载循环次数, N1 为裂纹外端达到盖板边缘时的荷载循环次数, N2 为盖板贯穿壁厚时荷载循环次数, N3为试件刚度退化 25% 时荷载循环次数。

三、基于结构应力法的疲劳寿命分析
1、有限元模型建立
由于结构几何并不复杂,可以通过2D有限元模型对结构进行近似计算,对于该结构的三维有限元及相应的疲劳分析见文献[4]。利用ABAQUS软件对结构进行建模,模型结果如下:
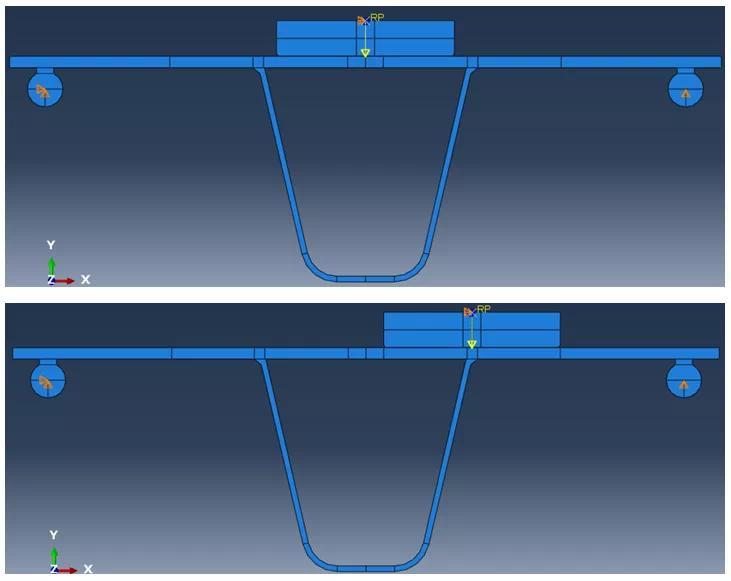
- 1)结构应力方法可以充分反应模型的边界条件和载荷影响,因此为保证计算结果的可靠性,需要保证模型的载荷和边界条件设置尽量符合试验中的加载和约束情况。例如本文采用简支边界条件,与文献[3]中的实验条件相符。并且模型模拟了橡胶垫块的效果,而没有把载荷简化成均布力直接施加到OSD钢桥上;
- 2)主S-N曲线是基于大量焊接接头的疲劳数据利用结构应力参数生成的疲劳曲线,因此焊接过程带来的影响(诸如残余应力等)都被隐式的考虑在了疲劳曲线(主S-N曲线)中,因此不需要对残余应力进行单独考虑,有限元模型也不需要模拟焊接过程,只要保证模型的几何形式与实际接头相符即可;
- 3)对于高周疲劳,接头的宏观变形情况是弹性变形,因此系统为线性系统,所以只需要计算单位载荷下接头位置的结构应力即可,其他载荷的结构应力可以等比例缩放。
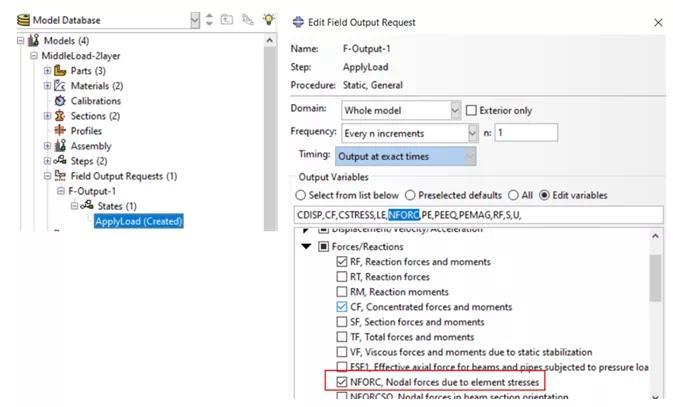
由于结构应力的计算方法是基于节点力和隔离体概念,所以在有限元计算提交之前要定义节点力的输出,在ABAQUS软件中,从 “Field Output Requests” 选项卡中输出NFORC变量,具体方法如图 4:一般来说,结构应力对网格不敏感(mesh insensitive),但是并不是与网格和单元划分彻底不相关(不是mesh independent),有限元网格的单元类型和网格尺寸应该保证模型对节点位移计算是准确的。例如在本文描述的试验条件下,由于钢桥产生明显的弯曲变形,因此如果用网格尺寸比较大的线性单元计算会产生明显的剪切自锁现象,因此采用二次单元进行分析。2、通过对有限元结果进行后处理计算结构应力
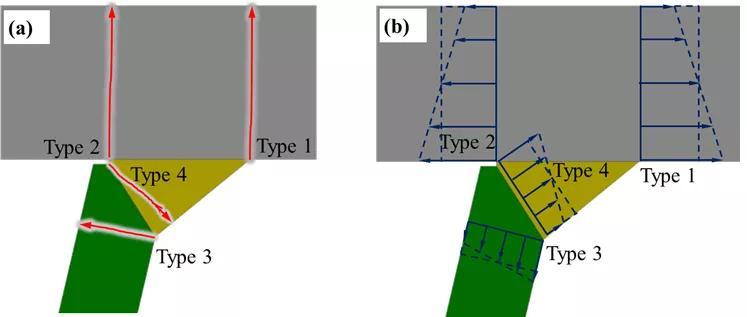
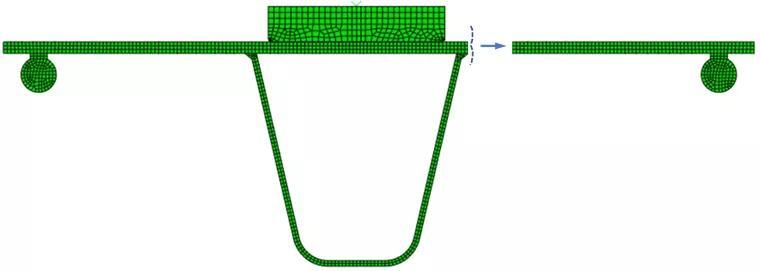
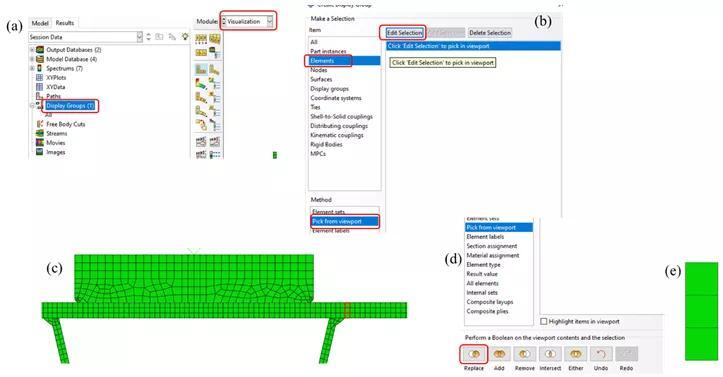
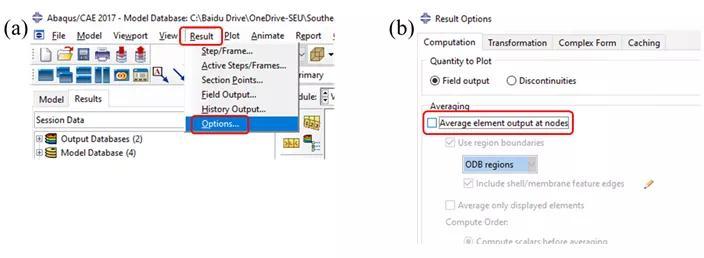
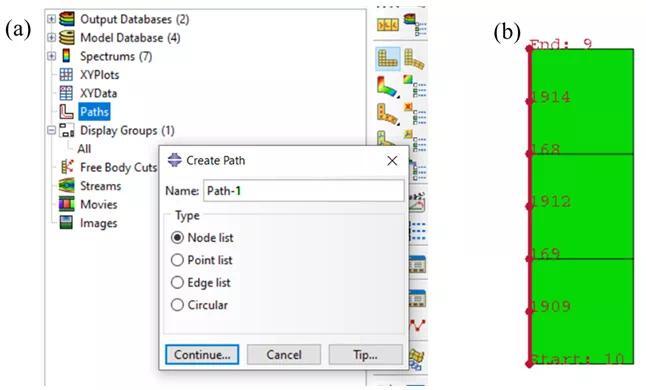
在有限元计算完成之后,可以计算OSD钢桥的结构应力,并据此进行疲劳寿命分析。首先需要强调的是结构应力属于traction stress (中文一般翻译为“斜面应力”),与应力张量(stress tensor)不同。有限元输出的结果一般是应力张量的某个分量(例如S11, S22, S33,S12, S23, S13),或者应力张量的不变量(例如各个主应力,米塞斯应力等),而traction stress定义则是基于材料力学最基本的“隔离体分析”(free body cut)概念,用一个假象的“斜面”(或平面)把结构切开,描述斜面两侧材料间的相互作用。隔离体分析是计算结构应力的核心,所以准确定义隔离体的切面是结构应力分析的关键。在结构疲劳计算中,这一切面一般为裂纹所在平面。以OSD钢桥的焊趾疲劳破坏为例,根据焊接结构的疲劳失效特性可知,焊趾破坏的裂纹一般从焊趾处萌生, 然后沿垂直板厚方向扩展,如图 5a中Type 1所示。由于本文分析的疲劳试验均为Type 1类型失效,(见图 6)本文只指针对Type 1的失效模式进行示例分析,其他失效模式计算方法大同小异。图5(a) 典型OSD钢桥焊接位置破坏模式(b)各个破坏模式对应的结构应力本分析中,OSD钢桥Type 1 失效对应的隔离体图如图 7所示。在ABAQUS有限元后处理中,隔离体的操作可以通过建立Display Group实现。具体操作流程为在Visualization Elements pick from viewpoint edit selection 中选中如图 8c红色轮廓的单元 Replace。整体操作流程如图 8所示,最终选中单元如图 8e。图 8 ABAQUS中通过Displacement Group 建立隔离体图的方法在利用节点力(NFORC)计算结构应力首先需要对有限元模型中各节点的应力计算进行简要说明:一般来说对于常规应力分量,有限元计算首先计算出各个单元积分点处的应力数值,然后外插到单元的节点处。对于某个节点,它可能连接若干单元,那么一般来讲,该节点的应力是它连接单元在此节点外插应力的平均值。不同有限元软件(或后处理软件)的平均值计算方法可能不同。但是结构应力的计算与此不同,因为在有限元静力分析中,节点力是基于平衡条件计算的,这意味着在某个节点,所有连接这个节点的单元在这一节点上的合力为0,因此平均值也为0,所以在利用节点力计算结构应力时首先要取消软件默认的平均值计算选项,具体操作步骤为:在Visualization模块下,Result Options 勾除 Average element output at nodes 选项,如图 9所示。随后应当定义计算结构应力的路径,可以通过ABAQUS后处理中定义Path(路径)来实现,具体方法如图 10:Paths Node list Continue 选择节点,如图 10b。这里需要注意的是,由于选取了二次单元,所以单元内部也有节点,比如节点1909、1912、1914,选择时候不要忘记漏选。在选取好裂纹路径后,即可输出节点力,具体操作如图 11所示。
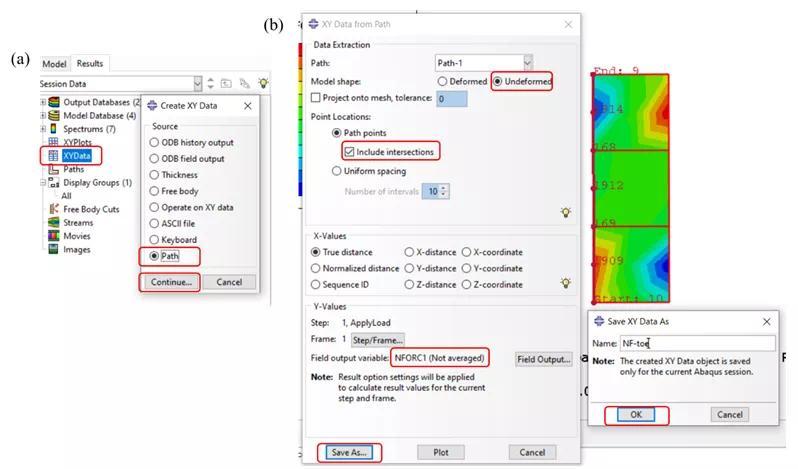
在提取节点力后,可以在ABAQUS右侧的XYData中进行编辑并复 制到excel(或其他计算工具如matlab等)中进行结构应力计算具体操作如图 12所示。值得注意的是,如果ABAQUS 6.14版本可能不支持从ABAQUS直接复 制粘贴操作,遇到这种情况可以通过Plug-ins Tools Excel Utilities 导出。二维问题中,可以利用公式计算结构应力,其中 的符号由具体坐标系和路径的坐标原点确定:
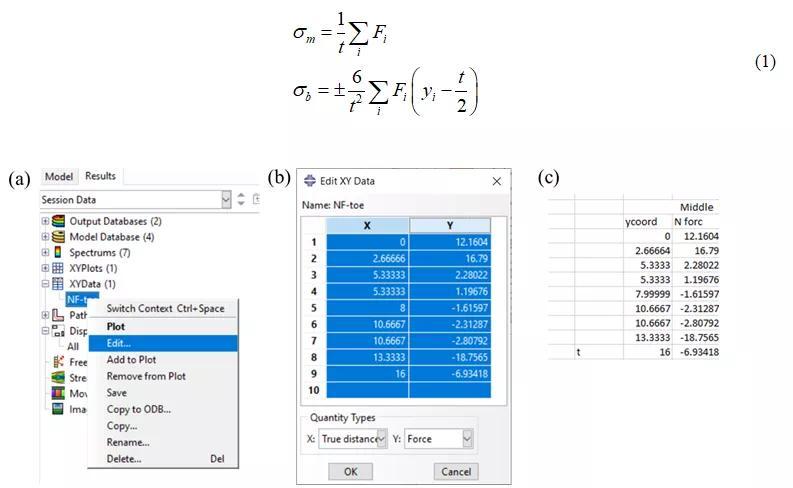
图12(a)编辑节点力(b)ABAQUS中节点力输出(c) 复 制节点力到excel表格

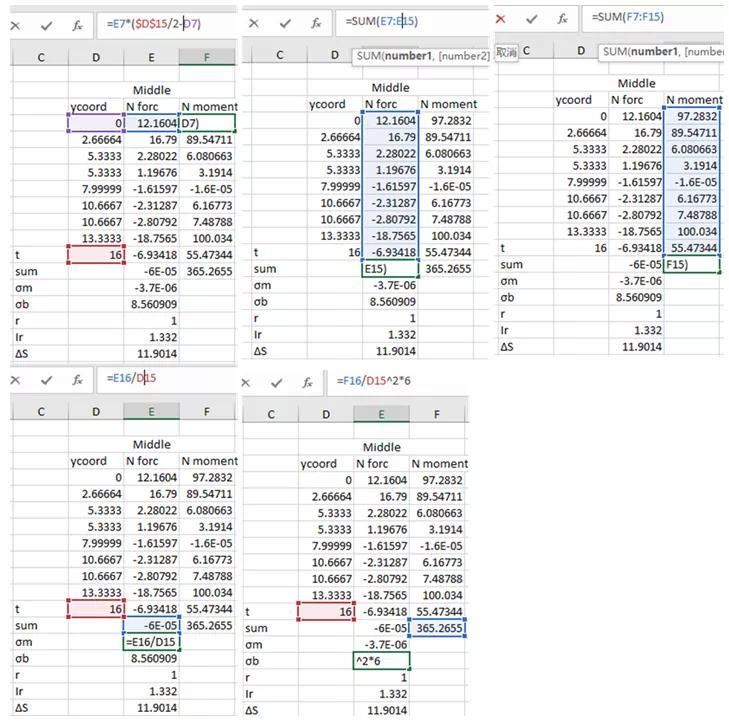
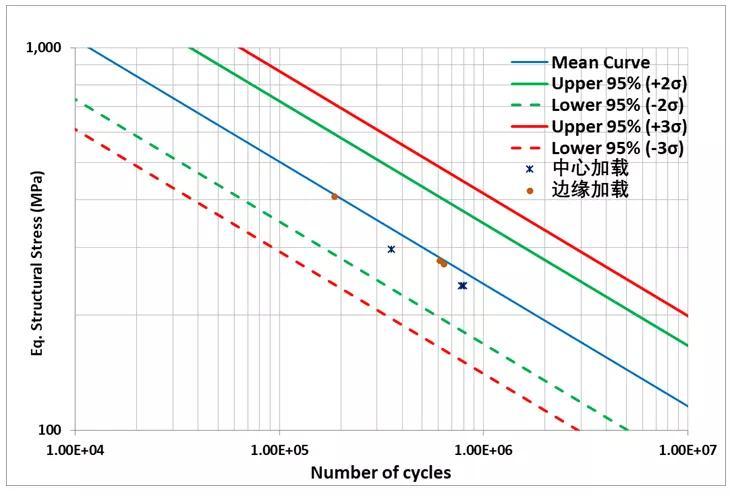
根据公式计算得到两种试验模式下,OSD钢桥焊趾处结构应力数值在表格 3中给出。注意表格中计算得到的结构应力是对应于单位载荷(1kN)的结构应力大小。对于实际载荷,由于构件发生高周疲劳,系统属于线性系统,只需要对结构应力根据实际载荷进行等比例缩放即可,得到结果如表格 4所示。在得到等效结构应力后,可以将对应的 数据绘制到主S-N曲线上去,得到的结果如图 14所示。从图中可以看出,试验数据点均在主S-N曲线的均值曲线(Mean Curve)附近。这从一个侧面证明了可以看出结构应力 主S-N曲线对焊接结构的疲劳预测的可靠性。
表格 3 单位载荷(1kN)下两种加载模式对应的等效结构应力
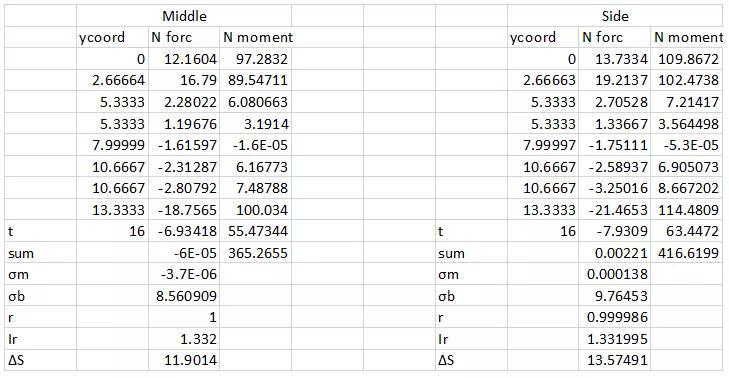
表格 4 实际载荷下各试件的结构应力和疲劳寿命预测情况
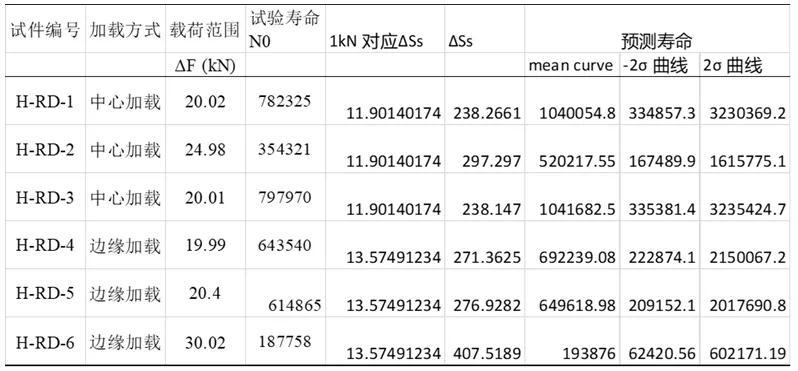
此外,根据主S-N曲线,等效结构应力与疲劳寿命之间的关系为:根据公式,可以根据计算得到的等效结构应力预测结构的疲劳寿命,预测的疲劳寿命与试验寿命对比如图 15所示。可以看出,试验寿命与主S-N的均值曲线预测寿命接近,并且都在 曲线预测得到的疲劳寿命之间。图15结构应力 主S-N曲线预测寿命与试验寿命对比四、小结
本文以OSD钢桥焊趾疲劳破坏为例,详细介绍了利用二维有限元模型进行结构应力计算以及基于主S-N曲线进行疲劳分析的具体步骤。笔者后续会在仿真秀官网和仿真秀App个人专栏-WeldMech上传视频教程,讲解这一实例的具体操作方法。根据同行需求也可能推出利用三维有限元模型计算结构应力及疲劳分析的相关视频教程,欢迎各位同行和专家不吝赐教、批评指正,共同进步。
参考文献
[1] 董磊, 崔慕春, 三桥刚性矿车车架的疲劳寿命分析及优化, 自动化应用, (2021) 138-140.
[2] 叶星汉, 曹一山, 曹星儿, 程斌, 正交异性钢桥面板U肋-盖板焊接节点的疲劳性能试验, 公路交通科技, 34 (2017) 68-75.
[3] B. Cheng, X. Ye, X. Cao, D.D. Mbako, Y. Cao, Experimental study on fatigue failure of rib-to-deck welded connections in orthotropic steel bridge decks, International Journal of Fatigue, 103 (2017) 157-167.
- [4] P. Wang, X. Pei, P. Dong, S. Song, Traction structural stress analysis of fatigue behaviors of rib-to-deck joints in orthotropic bridge deck, International Journal of Fatigue, 125 (2019) 11-22.
(完)
作者简介:裴宪军博士 东南大学副研究员 仿真秀专栏作者
哈尔滨工业大学焊接技术与工程专业本科, 密歇根大学船舶与海洋工程专业博士,博士期间师从国际著名焊接结构专家董平沙教授。曾担任斯伦贝谢道尔实验室研究员,密歇根大学助理研究员工作,现任东南大学机械工程学院副研究员。
长期从事焊接结构疲劳断裂行为、结构完整性研究、材料加工(焊接/连接)等方面研究,取得了多项创新成果。参与了美国机械工程师学会(ASME)中设计焊接接头疲劳分析的修订工作。发表各类论文30余篇,申请国际专利两项。
声明:原创作品,首发仿真秀App,部分图片和内容源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。