微分方程边值Matlab求解实例
本文摘要(由AI生成):
本文介绍了如何使用MATLAB中的bvp4c函数求解边值问题(BVP)的解。首先,文章解释了odefun、bcfun和sinit等关键概念及其作用。然后,详细说明了sol结构中的各个字段的含义。接着,文章介绍了如何使用bvpinit函数来初始化猜测解,并给出了在不同情况下的使用方法。之后,文章解释了如何使用deval函数来评估特定点的解。最后,文章通过一个具体示例展示了如何应用这些函数来求解BVP的解,并给出了相关的绘图代码。对于复杂问题,文章建议采用偏微分原理进行自编程序求解,并提到了常用的差分法和Runge-Kutta法。
常微分方程一阶方程组边值问题Matlab的标准提法为:
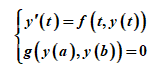
Matlab中有自带求解边值问题函数。bvp4c;bvpinit
sol = bvp4c(odefun,bcfun,solinit)
sol = bvp4c(odefun,bcfun,solinit,options)
sol = bvp4c(odefun,bcfun,solinit,options,pl,p2..)
odefun是微分方程组函数;bcfun为边值条件函数;sinit是由bvpinit得到的粗略解网络
求的边值问题解。
sol结构:
sol.x | bvp4c 选择的网格 |
sol.y | 在网格节点sol.x处的y(x)的近似值 |
sol.yp | 在网格节点sol.x处的y`(x)的近似值 |
sol.parameters | 可能情况下是bvpc为未知系数返回的值 |
sol.solver | ‘bvp4c’ |
solinit = bvpinit(x,v)
x是一个定义初始网格向量。如果用户希望在区间[a, b]上求解边值问题(BVP),则定义x(1)为a,x(end)为b。函数bvp4c 为求解调整该网格,所以通常如x = linspace(a,b,10)的猜测值就能够满足要求。在一些比较困难情况下,用户必须在变化剧烈点上布置网格结点。而x中的各项则必须进行编号且各不相同,所以如果a<b则x(1)<x(2)<...<x(end)。
v是猜测值。既可以是向量,也可以是函数:
solinit = bvpinit(x,v,parameters)
表明方程中含有未知参数。使用向量parameters提供所有未知参数的可能值。
solinit = bvpinit(sol,[anew bnew])
根据原方程在区间[a,b]上对应解 sol ,在新区间[anew bnew]上生成新的初始解
sxint.=deval(slo,xint)
使用函数deval和sol可以求解在区间[a,b]上的特定点xint对应的解。
应用上述三个函数求具体解
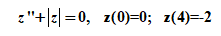
令y(1)=z,y(2)=z’ 则方程为:

边界条件
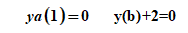
clear
sinit=bvpinit(0:4,[1;0])
odefun=inline('[y(2);-abs(y(1))]','t','y');
bcfun=inline('[ya(1);yb(1) 2]','ya','yb');
sol=bvp4c(odefun,bcfun,sinit)
t=linspace(0,4,101);
y=deval(sol,t)
figure1 = figure;
axes1 = axes('Parent',figure1);
hold(axes1,'on');
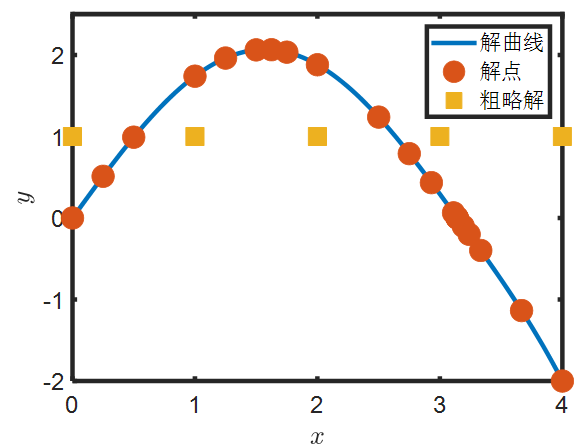
plot(t,y(1,:),'DisplayName','解曲线','LineWidth',3);
plot(sol.x,sol.y(1,:),'DisplayName','解点','MarkerFaceColor',[0.850980401039124 0.325490206480026 0.0980392172932625],...
'MarkerSize',15,...
'Marker','o',...
'LineStyle','none');
plot(sinit.x,sinit.y(1,:),'DisplayName','粗略解','MarkerFaceColor',[0.929411768913269 0.694117665290833 0.125490203499794],'MarkerSize',15,...
'Marker','square',...
'LineStyle','none');
ylabel('$y$','FontSize',20,'Interpreter','latex');
xlabel('$x$','HorizontalAlignment','center','FontSize',20,'Interpreter','latex');
ylim(axes1,[-2 2.5]);
box(axes1,'on');
hold(axes1,'off');
set(axes1,'FontSize',16,'LineWidth',3,'TickLength',[0.005 1]);
legend(axes1,'show')完美实现满足边界条件的x-y值,对于简单问题可以采用上述方式,对于复杂问题,需要更加偏微分原理进行自编程序求解,常用的方法有差分法和Runge-Kutta法,由于方法细节比较多,本期过冷就先给大家讲这么多,微分原理之后再讲。





