非线性可视化（4）庞加莱截面

3年前浏览6400

上一期介绍了几个经典的非线性系统，并给出了他们在三维相空间的各种表现。

但是随着维度增加到三维甚至更高维，光绘制出相空间已经不足以直观的了解系统的形态。我们也很难对着一坨烂七八糟的轨线在论文里水字数。因此有必要引入一个新的可视化方法，对系统进一步降维，提炼出更简洁的信息。

庞加莱截面就是基于这个思想被提出来的。对于一个周期运动的系统，在相空间的运动表现为一圈又一圈的转动。我们定义一个截面（一般是平面），当轨线穿过这个面时，把交点记录下来。当记录足够多的交点后，这些交点形成的图像就是庞加莱截面的图像。而这个截面就是庞加莱截面。

一般只记录由向正向负穿越截面的交点，不记录由负向正穿越的点。这样，就可以得到下面的规律：对于单周期运动，轨线为一个近似圆形，庞加莱截面上为一个点；对于2周期运动，轨线绕两圈才会闭合，穿过庞加莱截面两次，表现为2个点；对于周期N的运动，庞加莱截面上有N个点。

对于混沌运动，截面上的点理论上会有无限多。如果截面上的点形成了一条线，则把这种运动叫做拟周期运动。如果庞加莱截面上的点形成了一片二维图形，甚至还存在分形结构，则可以判断是典型的混沌运动。

单纯的说可能不太直观，这里用之前的duffing方程举个例子。

将Duffing方程改写为下面的三维形式：

然后和前面一样，用龙格库塔方法求解即可。

取[δ,γ,ω]=[1.5,1,1]，其三维的相空间和对应的庞佳莱截面如下：

三维的轨线图为近似一个圆。绿色的面就是定义的庞加莱截面（当然实际上应该是一个无限大的平面，这里为了展示只画了一部分）。这时对应的运动为典型的周期运动，庞加莱截面上只有一个交点。

当取[δ,γ,ω]=[1.35,1,1]时，其三维的相空间和对应的庞佳莱截面如下：

此时的运动变为周期2的运动，对应的二维相平面上的投影（下面黑色的），为一个交叉的双环。这种周期2的运动与庞加莱截面有2个交点。

当取[δ,γ,ω]=[1.15,1,1]时，其三维的相空间和对应的庞佳莱截面如下：

此时运动变为混沌运动，对应的二维相平面投影为一个混沌的8字型堆叠的图案。而庞加莱截面上的点则似乎很有规律的分布着。

单独将截面上的点绘制出来，可以得到：

庞加莱截面上的点以线的方式分布着，可以认为这种运动为一种准周期运动。

如果取[δ,γ,ω]=[0.1,0.35,1.4]时，系统会进入混沌状态，其庞加莱截面演示图如下：

其庞加莱截面图像如下。对于复杂的庞加莱截面，如果想要绘制的好看，需要计算非常多的点，这也意味着非常大的计算时间。

此时，庞加莱截面还有很多分形结构，其局部放大图如下

计算庞加莱截面的方法可以分为两步：1计算出轨线 2计算出线与面的交点。

额外插一句，Duffing方程如果翻到开头，去看它的形式，可以看到它是一个非自治系统，有一个周期性外力在方程里。这里绘制庞加莱截面的处理方式，是把周期性力单独提出来，定义为z，然后绘制z=0的图像。这时每个截面上的点对应时间t，是一个以周期（2π/ω）为等差的数列。

还有一种降维方法，叫做频闪采样法，就是针对这类型含有周期驱动力的方程的。在计算完轨线之后，直接取t0,t0 T,t0 2T,t0 3T,...这样的时间序列，其中T为驱动周期，这些点天然的在一个庞加莱平面上。因此，这样可以大大的简化庞加莱图像的计算，缩短计算时间。方程本身甚至也可以降维到2维，如下面所示。虽然下面的方程已经看不到高维空间截面的样子，但是频闪采用法本质上还是庞加莱截面。

下面程序是通用的计算庞加莱截面的matlab程序：

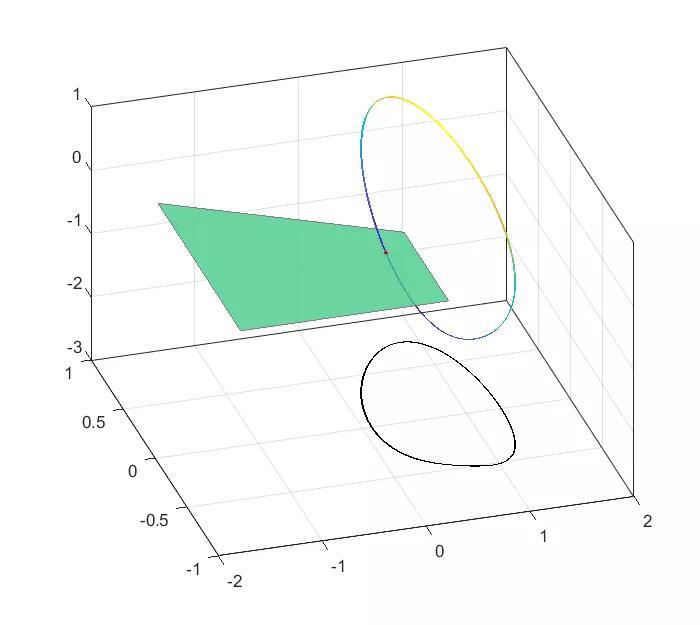
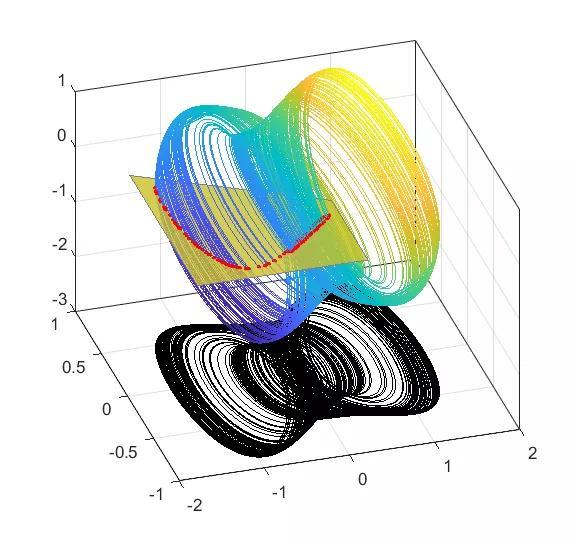
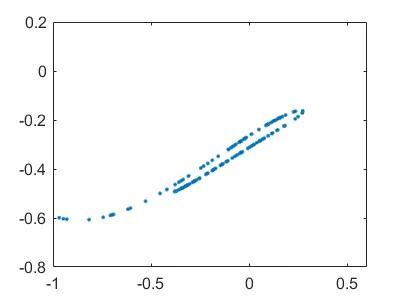
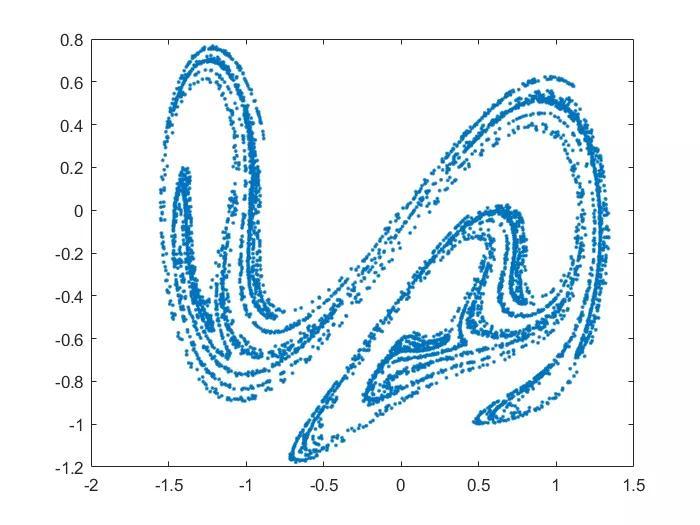
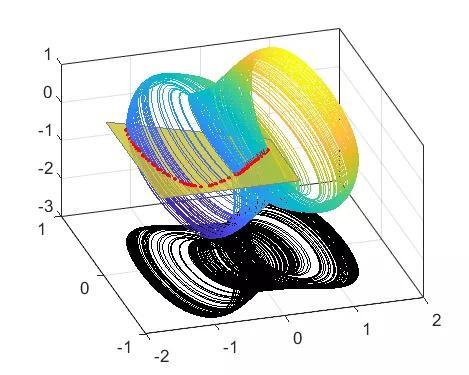
%庞佳莱截面%截面采用公式Ax By Cz D=0;的形式%采用杜芬方程演示clearclcclose all%第一步，计算出轨迹h=5e-3;x0=0:h:1600;y0=[0.1;0.1;1];%最后一项是cos(w*t)，当t=0时必须为1.[y1,Output]=ODE_RK4_hyh(x0,h,y0,[1.15,1,1]);%[1.5,1,1],[1.35,1,1],[1.15,1,1],[0.1,0.35,1.4]Lx=y1(1,2000:end);Ly=y1(2,2000:end);Lz=y1(3,2000:end);
Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面。这里是z=0[tP_List,yP_List]=Solve_Poincare(x0,y1,Plane);%计算Poincare平面上的点
%绘图%1庞加莱截面%最开始几个点还没有稳定，没有体现出系统特点，所以放弃，从第10个点开始figure()plot(yP_List(1,10:end),yP_List(2,10:end),'.')xlim([-1,0.6])ylim([-0.8,0.2])
%2投影的二维相平面figure()plot(Lx,Ly)
%3展示用的示意图figure()hold onpatch([Lx,nan],[Ly,nan],[Lz,nan],[Lx Ly,nan],...    'EdgeColor','interp','Marker','none','MarkerFaceColor','flat','LineWidth',0.8,'FaceAlpha',1);plot3(yP_List(1,10:end),yP_List(2,10:end),zeros(size(yP_List(2,10:end))),...    '.','MarkerSize',8,'color','r')patch([-1.6,0.4,0.4,-1.6],[-0.7,-0.7,0.0,0.6],[0,0,0,0],[1,1,1,1],...    'FaceAlpha',0.8,'EdgeColor',[0.5,0.5,0.5]) view([-17,39])box ongrid on%绘制相图set(gcf,'position',[300 200 560 500])xlim([-2,2])zlim([-3,1])plot3( Lx,Ly,zeros(size(Ly))-3 ,'color','k')hold off

function [tP_List,yP_List]=Solve_Poincare(t,y,Plane)%截面方程z=0% Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面%一般只记录从负到正穿越。如果想反向也记录，可以设置Plane=-Plane。%第一步，计算出轨线y%第二步，插值得到线与面的交点yP_List=[];tP_List=[];Dis=DistancePlane(y,Plane);N=size(y,2);for k=1:N-1    if Dis(k)<=0 && Dis(k 1)>0        t0=t(k);t1=t(k 1);        yP0=y(:,k);yP1=y(:,k 1);        Dis0=Dis(k);Dis1=Dis(k 1);        %一维线性插值，求Dis=0时的t和y        %（相比较前面积分的4阶RK，这里用线性插值精度有点低）        yP=yP0 (yP1-yP0)/(Dis1-Dis0)*(0-Dis0);        tP=t0 (t1-t0)/(Dis1-Dis0)*(0-Dis0);        %储存        yP_List=[yP_List,yP];        tP_List=[tP_List,tP];    endendend

%点到平面的距离function Dis=DistancePlane(xk,Plane)% xk，坐标点，如果是3维坐标，大小就是3*N的矩阵。% Plane，平面，形如Ax By Cz D=0形式的平面。
N=size(xk,2);%计算总共多少个点xk2=[xk;ones(1,N)];Dis=dot(xk2,Plane*ones(1,N),1)./norm(Plane(1:end-1));end
%两点线性插值function y=interp2point_linear(x0,x1,y0,y1,x)y=y0 (y1-y0)/(x1-x0)*(x-x0);end
%两点3次插值function y=interp2point_spline(x0,x1,y0,y1,x)%y0包含y0的值和y0的导数,yy=y0(1),dy=y0(2)xx0=x0;xx1=x1;yy0=y0(1);dy0=y0(2);yy1=y1(1);dy1=y1(2);cs = csape([xx0,xx1],[dy0,yy0,yy1,dy1],[1,1]);y=ppval(cs,x);end
function [F,Output]=Fdydx(x,y,Input)%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数%杜芬方程duffing，参见中国大学MOOC，北京师范大学-计算物理基础-77倒摆与杜芬方程d=Input(1);r=Input(2);w=Input(3);
dy(1)=y(2);dy(2)=-y(1)^3 y(1)-d*y(2) r*y(3);dy(3)=-w*sin(w*x);
F=[dy(1);dy(2);dy(3)];Output=[];end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)%4阶RK方法%h间隔为常数的算法y=zeros(size(y0,1),size(x,2));y(:,1)=y0;for ii=1:length(x)-1    yn=y(:,ii);    xn=x(ii);    [K1,~]=Fdydx(xn    ,yn       ,Input);    [K2,~]=Fdydx(xn h/2,yn h/2*K1,Input);    [K3,~]=Fdydx(xn h/2,yn h/2*K2,Input);    [K4,~]=Fdydx(xn h  ,yn h*K3  ,Input);    y(:,ii 1)=yn h/6*(K1 2*K2 2*K3 K4);endOutput=[];end

下面是相同效果下，采用频闪采样法。Duffing方程也被降维为2维（其实也可以不变）

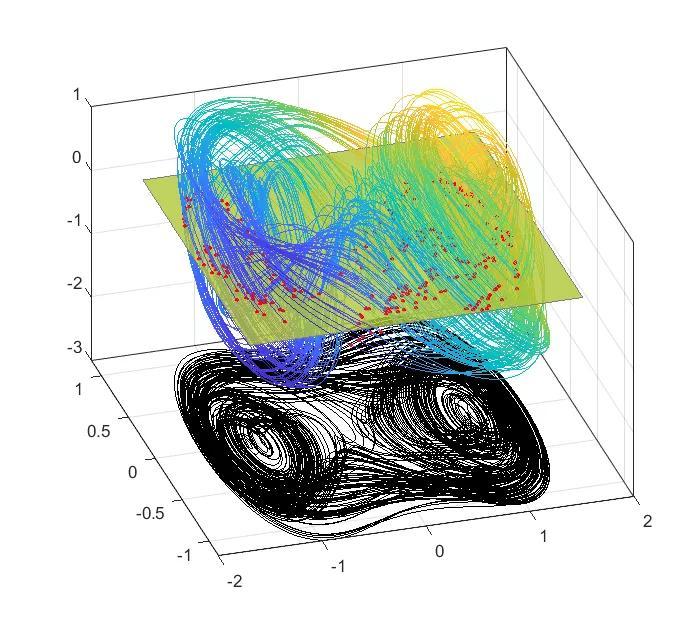
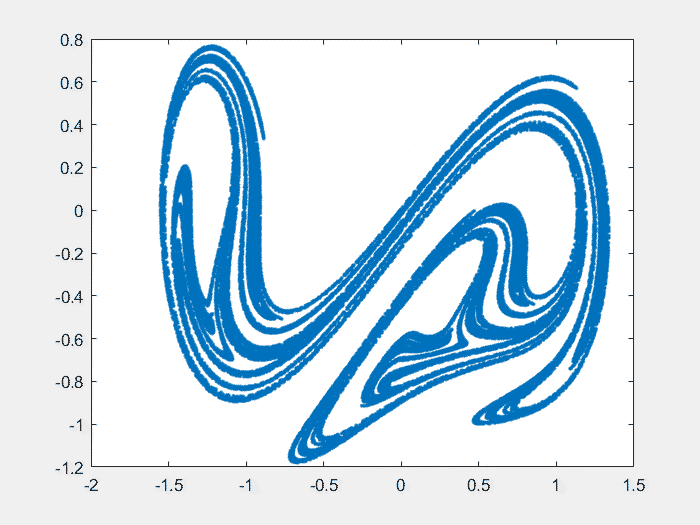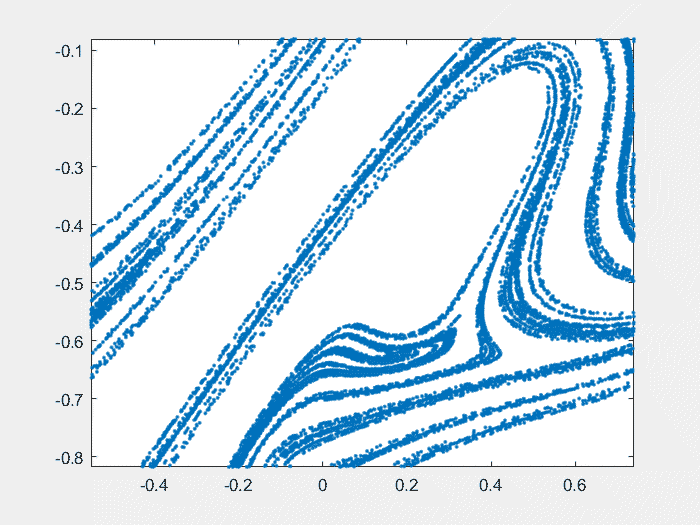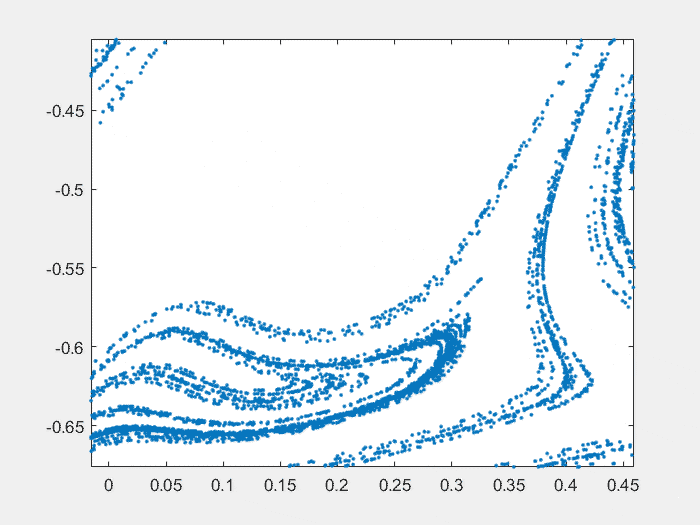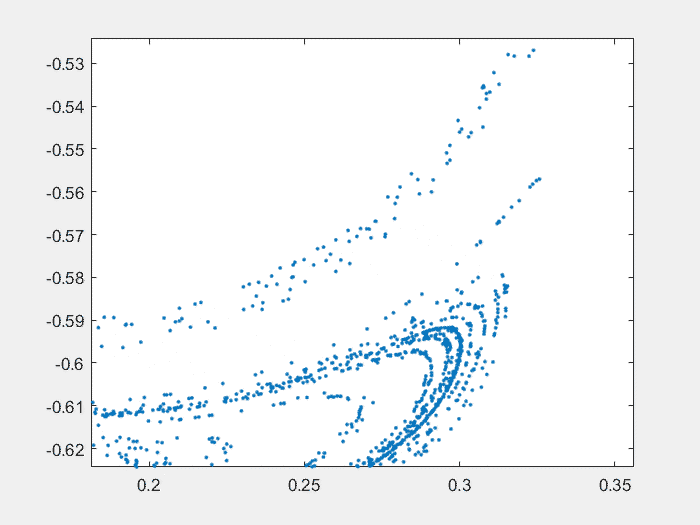
%庞佳莱截面%截面采用频闪采样法%采用杜芬方程clearclcclose all%第一步，计算出轨迹h=5e-3;x0=0:h:1600;y0=[0.1;0.1];%最后一项是cos(w*t)，当t=0时必须为1.[y1,Output]=ODE_RK4_hyh(x0,h,y0,[1.15,1,1]);Lx=y1(1,:);Ly=y1(2,:);Lz=cos(1*x0);%不用计算截面的方式% Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面% [tP_List,yP_List]=Solve_Poincare(x0,y1,Plane);%计算Poincare平面%采用频闪采样法计算tP_Ideal=3*pi/2:(2*pi/1):x0(end);tP_List=zeros(1,length(tP_Ideal));Ind_List=zeros(1,length(tP_Ideal));for k=1:length(tP_Ideal)    [~,Ind]=min(abs( tP_Ideal(k)-x0 ));    Ind_List(k)=Ind;    tP_List(k)=x0(Ind);endyP_List=y1(:,Ind_List);
%绘图%3展示用的示意图figure()hold on% plot3(y1(1,:),y1(2,:),y1(3,:))patch([Lx,nan],[Ly,nan],[Lz,nan],[Lx Ly,nan],...    'EdgeColor','interp','Marker','none','MarkerFaceColor','flat','LineWidth',0.8,'FaceAlpha',1);plot3(yP_List(1,10:end),yP_List(2,10:end),zeros(size(yP_List(2,10:end))),...    '.','MarkerSize',8,'color','r')patch([-1.6,0.4,0.4,-1.6],[-0.7,-0.7,0.0,0.6],[0,0,0,0],[1,1,1,1],...    'FaceAlpha',0.8,'EdgeColor',[0.5,0.5,0.5]) view([-17,39])box ongrid on%绘制相图set(gcf,'position',[300 200 560 500])xlim([-2,2])zlim([-3,1])plot3( Lx,Ly,zeros(size(Ly))-3 ,'color','k')hold off
function [F,Output]=Fdydx(x,y,Input)%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数d=Input(1);r=Input(2);w=Input(3);%降维后的Duffing方程dy(1)=y(2);dy(2)=-y(1)^3 y(1)-d*y(2) r*cos(w*x);% dy(3)=-w*sin(w*x);F=[dy(1);dy(2)];Output=[];end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)%4阶RK方法%h间隔为常数的算法y=zeros(size(y0,1),size(x,2));y(:,1)=y0;for ii=1:length(x)-1    yn=y(:,ii);    xn=x(ii);    [K1,~]=Fdydx(xn    ,yn       ,Input);    [K2,~]=Fdydx(xn h/2,yn h/2*K1,Input);    [K3,~]=Fdydx(xn h/2,yn h/2*K2,Input);    [K4,~]=Fdydx(xn h  ,yn h*K3  ,Input);    y(:,ii 1)=yn h/6*(K1 2*K2 2*K3 K4);endOutput=[];end

效果图如下，可以看到两种方法是一致的。

频闪采样法适合周期驱动的非自治方程。而一般形式的庞加莱截面求交点法，试用范围会更广一些。

理论科普多尺度非线性

著作权归作者所有，欢迎分享，未经许可，不得转载

首次发布时间：2021-12-08