本节主要技能点：

1、不同影响松脱扭矩结果因素的横向对比计算；

2、载荷步控制方法及仿真收敛性评价方法；

3、压装力仿真计算方法简介

（接上节）以上设置完成，复 制相同类型的Case，并微调其不同设置，如摩擦系数为0.1、0.09、0.08等，一直到0.03共计8组重复计算。而后设置20个核心并行（求解本案例计算机，采用测试版Intel志强8272处理器。其拥有26个物理核心及52线程）。保存项目文件，开始求解。一般而言，仿真时设置80%~90%物理核心数量，且关闭CPU的超线程技术后，单次单Case的综合计算效率最高。如需同时计算两个Case，建议另存为其他计算文件，并同时打开两组互相独立的Case，并将每一个计算文件设置40%左右计算机物理核心的并行数量，可达到较高的综合效率。原则上不建议，采用以上方法同时求解2个以上的计算。因为限制于计算机硬盘速度及内存容量，一般更多Case将被拖后腿。

由于有限元分析的多核心并行计算效率较低，一般而言CPU拥有1核心~8核心时，基本随着核心数量增加，计算时间线性降低，8核心~16核心后，堆核心的加速效果逐渐下降，16核心~28核心时，计算时间提速极其有限直至不变。

故CPU选择依据为相同价位，尽量多的同时且按顺序满足，以下条件为佳：一颗CPU、功率最大、核心最少、单核心浮点运算性能最强、全核心满载频率最高、平均每个核心的三级缓存最大。

遗憾的是，从2010年广泛推行的GPU加速技术，也不适合于有限元分析。其综合性价比远低于再买一颗顶级CPU。同时，只有顶级专业显卡（Quadro品牌等）与任意型号专业GPU加速卡（Tesla品牌等），再搭配合理的驱动程序、操作系统、仿真软件版本等，方可用于ANSYS 的GPU加速。而绝大多数用户选用的，Geforce品牌的游戏用显卡，则无论价格为100元还是100万元，均对仿真求解无效。

下图为调试计算进度时，非常关键的信息来源。其包括力、扭矩、位移等收敛值。建议同时参考以上三个参数，并根据其曲线形状，判断是否需要调整计算。

其下方time为总体进度。如上文考虑扭矩与摩擦系数影响时，仅设置2个载荷步，则当前计算进度1.6242，为完成第一个载荷步，即过盈配合效应，正在计算第二载荷步，即过盈配合 扭矩载荷的影响，且完成到62.42%的进度。相当于达到100x62%=62N·m扭矩 过盈配合。

其右侧红色曲线，为不同载荷子步的收敛情况。如果其宏观趋势为逐渐升高，则认为当前计算进展良好。如出现大量水平方向延伸甚至向下持续变化，则说明计算出现明显故障，需立刻暂停排查，而不要继续浪费生命，等待求解。此时不要停止计算，将丢失所有中间数据，则故障排查无从谈起，应该选择暂停。

根据计算量与计算机硬盘速度等影响，单击暂停后的数分钟到一两个小时内，方可真正完成暂停操作。而后保存数据，并查看求解输出信息，检查具体报错原因。

笔者在第一部组著作《ANSYS Workbench结构工程高级应用》开篇第一章介绍，哪些用户不适合学习有限元，其中一条为完美主义者或者强迫症晚期。

红色曲线局部、细节、间隔的出现少量水平或向下，并不明显影响计算进程，反而是载荷子步的数量，选择合理的一种表现。请接受不那么完美的收敛曲线。

如载荷子步数量设置过大，且红色曲线平稳增加，虽然更有利于收敛，也说明计算进程十分完美，但计算量过于庞大，属于严重浪费生命的做法。应从少到多，逐渐增加载荷子步数量，从而在最低成本与最高精度的两极疯狂试探。

下图右上角部分，为细节的计算进程。其青色线为收敛标准，即力、变形、扭矩等的平衡条件。当紫色线与青色线交叉且低于其时，说明当前载荷子步计算收敛，结构处于外部载荷与约束处反作用力，基本平衡的条件。可继续加载下一个载荷子步，并出现绿色纵线提示，同时下面time处红色曲线，将略微向上提升。

如果一个载荷步内，如第一个蓝色纵线下方的3，说明仅仅借助，程序自动的3个载荷子步的加载，即完成了对过盈配合的计算进程，实现第一个载荷步的收敛。

相反的，如果本案例3个载荷子步，即可收敛的条件下，用户人为的在图-18中，将第一个载荷步，设置更多载荷子步去实现，如初始100最小40最大1000。通常是毫无意义的，浪费计算时间、浪费计算机硬盘空间、浪费用户生命的做法。

前文介绍过，需同时查看力、变形、扭矩三个参数的影响。如某一个或某两个参数的紫色曲线，如力与变形，长期处于青色线下方，但并未出现绿色子步收敛提示，概率而言第三个参数的紫色线，如扭矩必然长期高于青色线。需继续计算或暂停，并加密载荷子步。如图-18中，从100、30、1000变为200、100、1000。或查暂停看变形结果检查，确认是否有局部零件异常变形。

对于本文案例，核心目的为得到极限松脱扭矩。其过盈配合的接触状态，必然在扭矩增加到某一点时，发生异常变形，从而松脱崩溃，则计算结果必然出现，中途不收敛情况。此时未完成全部100N·m加载，反而是有利的（强迫症及完美主义者，哭晕在厕所），可说明设置最大100N·m扭矩设置正合适。否则应继续加大最大扭矩载荷，直到出现崩溃点为止。

这是一个多次调试的验证试算过程，可能会极大的增加计算量，同时计算进度变得不可控。建议从较为粗糙的网格尺寸开始尝试。

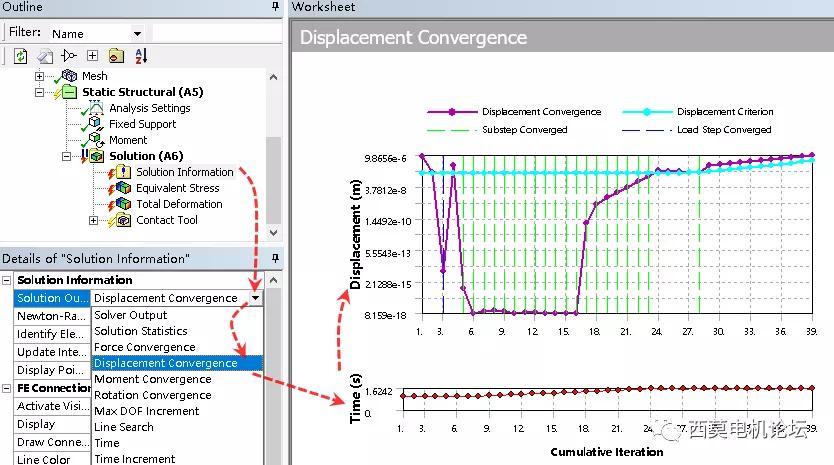
举一个极端且典型的案例。2021年8月22日，有网友B站私信问笔者，为什么其仿真时硬盘满了，并贴出下图。其极致密集的紫色曲线，已经完全掩盖了青色及绿色线的痕迹。同时右下角1.2663e5数据，说明当前计算已经完成了，12663次迭代计算。其相对本文上图中，39个子步即完成计算而言，计算次数差异，达到惊人的3100倍。

其下方红色time线，为十分平顺完美的倾斜射线。说明计算收敛十分完美，也暗示了载荷子步设置过于细腻，已经严重浪费计算时间。笔者在思考，这个用户的生命就这么不值钱，就这样肆意霍霍？果然年轻真好，

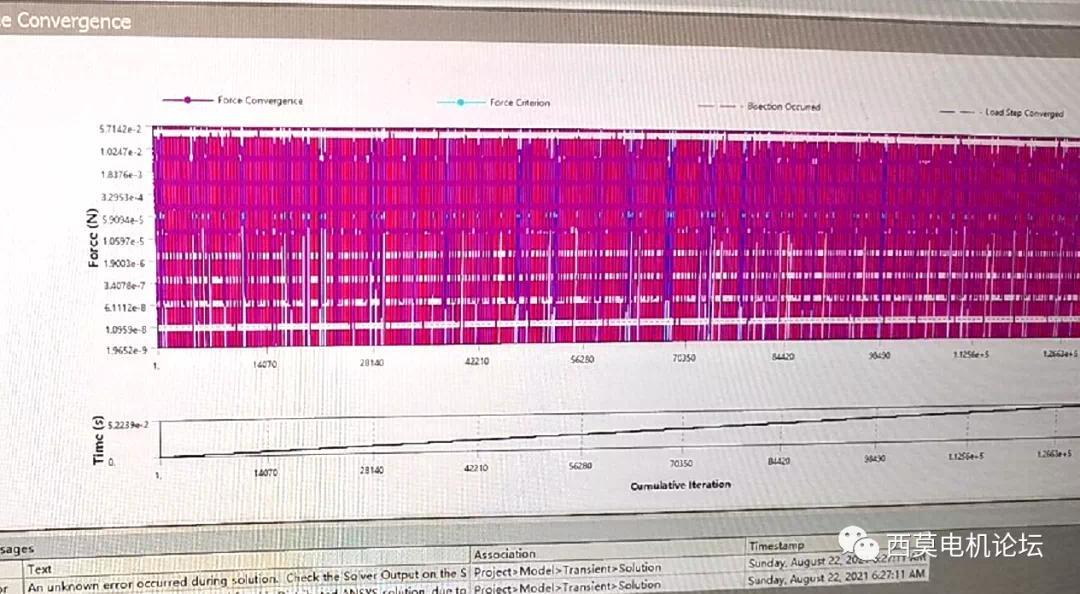
其左侧的计算模块与设置显示，采用瞬态动力学分析模块。加载自重与固定位移约束的同时，插入一段用户自定义的APDL语言。询问后提问者补充道，为300Hz正弦波脉冲电信号加载，以产生振动的计算。

令人印象深刻的载荷子步数量。

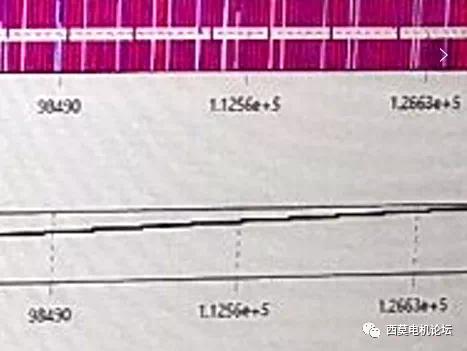
12万次迭代，触碰了笔者2010年自学仿真技术至今11年以来，最多瞬态迭代次数的眼界天花板。笔者不会debug不会say hello，只会心疼这提问的大哥。

计算完成后，保存项目文件并在结果中，右键提取接触结果。

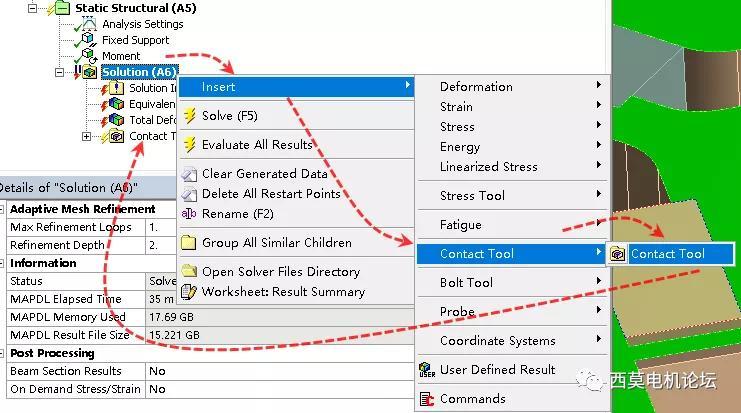
由于本案例仅设置1组摩擦接触，在右侧列表中已默认选择。如用户设置了大量接触，但仅需提取其中极少数几个，则需要手工的依次反选其他接触。这将是一项令人窒息的简单重复劳动工作，且其上方的add等功能，几乎没有成功奏效的一天。

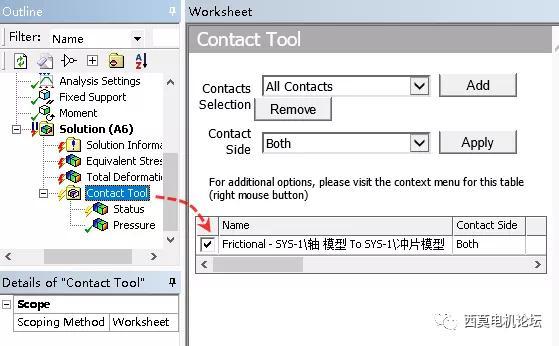
提取需要的接触结果。对于本案例，默认提取接触状态结果，也可根据用户需要，继续提取接触压力等结果。同时选择第二个黄色闪电的提取结果图标，而不是上方的求解图标。

这是因为当前计算，仅完成1.62time的进程，并未完全结束。如点选求解案例，为继续求解从1.62到2的后面部分。

对于本案例，其将是毫无意义的浪费生命。尤其是拥有大量复杂设置，且计算量较大时，仅仅误操作点选求解，而后立刻暂停并保存，用户往往也要多付出1小时~2小时的可贵生命。关键操作，请三思后行。

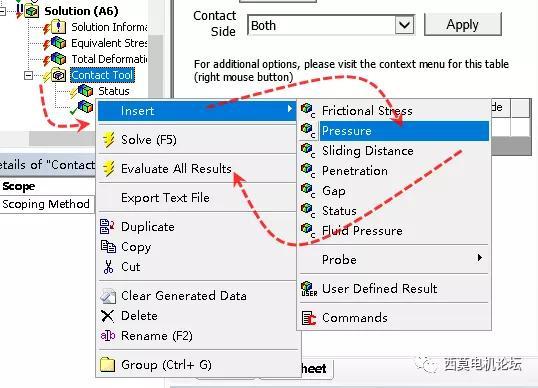
大部分情况下，默认的模型光照效果，并不清澈明快。建议如下图所示，将零件颜色、光照、渲染等参数适当加大，尤其汇报用截图时。

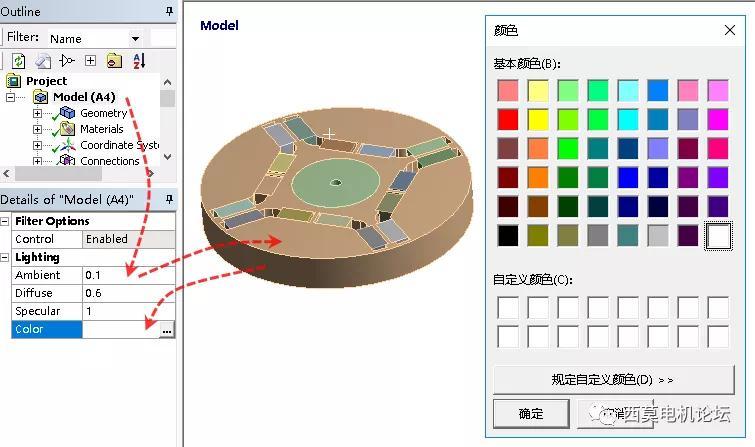
下图为仅调整一个参数后，模型颜色与上图的对比。

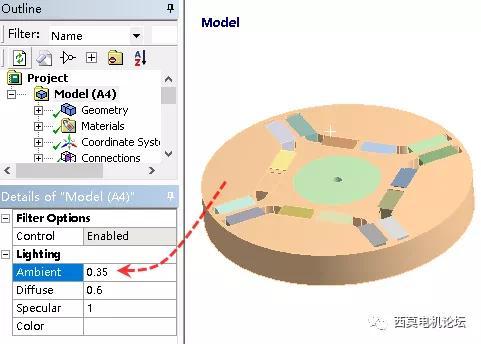
而后选中结果中的接触状态结果。其可在上方选择不同的结果显示方式。

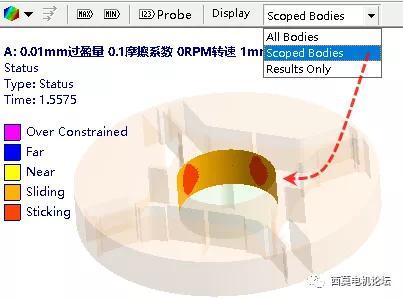
过盈配合表面的接触状态，随着从载荷步1到载荷步2，出现随扭矩的增加，而逐渐非线性变化的趋势，尤其是蓝色的平均接触压力结果。

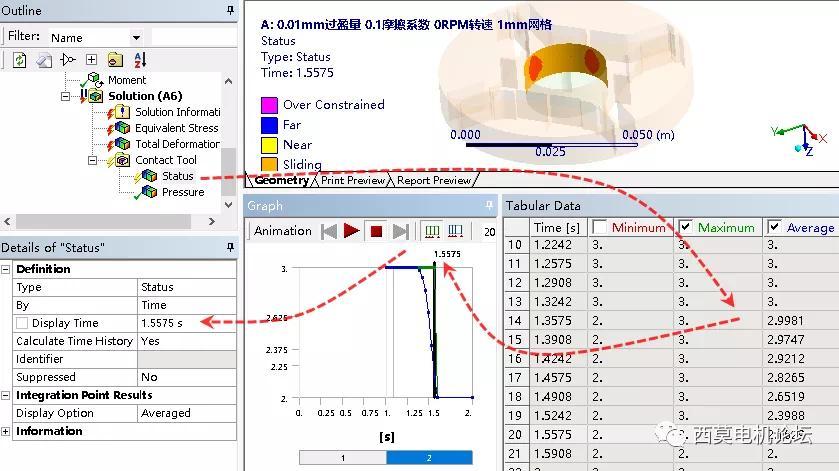
对于本图上方所示的工况：0.01mm过盈量、0.1摩擦系数、0RPM转速、1mm网格时，接触状态在1.5575时，最大接触状态出现从水平，到断崖式下降的突变。说明当前载荷，即100x0.5575=55.75N·m扭矩，为极限松脱扭矩。

由于当前载荷子步，过渡较为细腻，其占有屏幕面积较小，不利于观察与截图展示。可左键滑动，并右键局部放大显示。

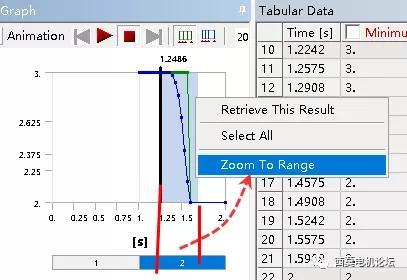
放大后，可更清晰显示各曲线的细节变化关系。以上功能还可用于生成结果动画时，局部截取之用。

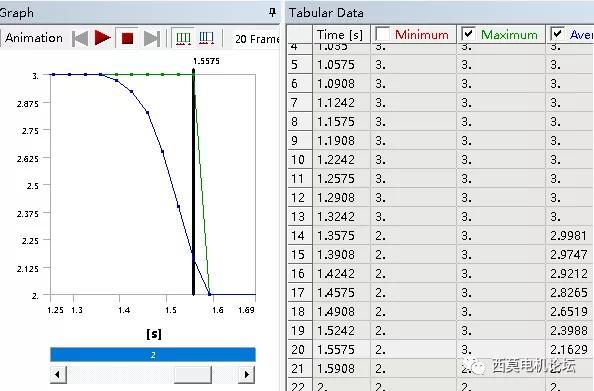
在其右侧表格中，可在左上角空白处，右键并提取为Excel文件，用于后续数据分析。

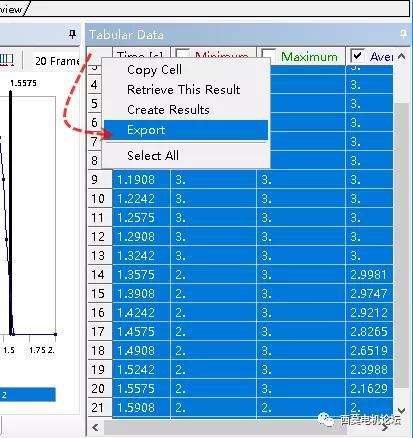
保存并命名该Excel文件。

绘制接触状态散点图。

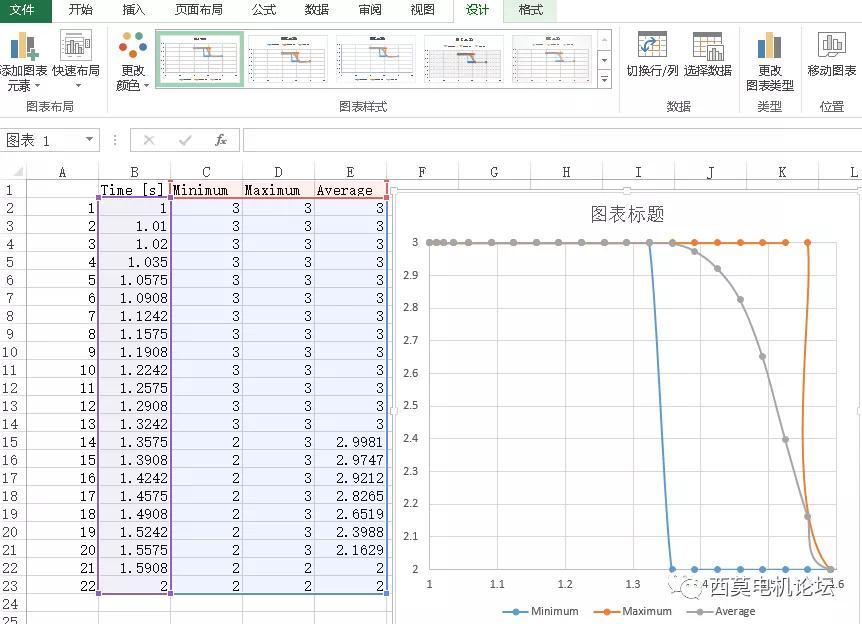
下面汇总松脱扭矩与各影响参数的变化关系曲线。

注，以下曲线中，散点均为原始数据，虚线均为线性外推结果。

摩擦系数与松脱扭矩间，呈线性下降趋势。

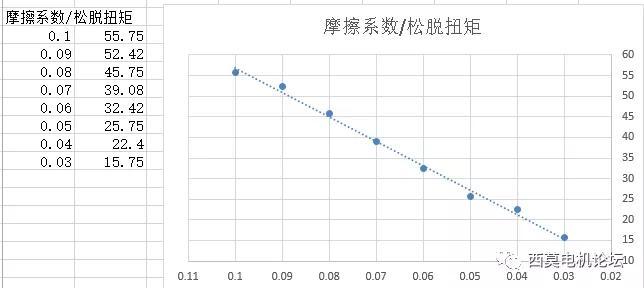
过盈量与松脱扭矩间，为线性增加趋势。

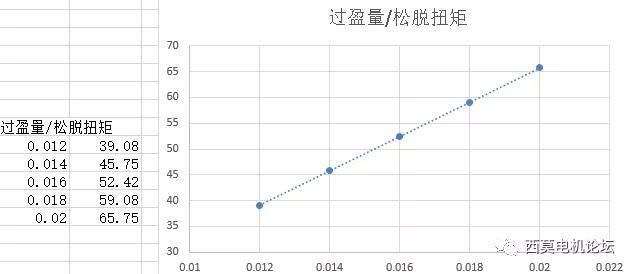
网格尺寸与松脱扭矩关系。令人十分意外的是，本案例中，即使网格尺寸有4倍左右的变化范围，依然出现结果与网格不变的尴尬局面。

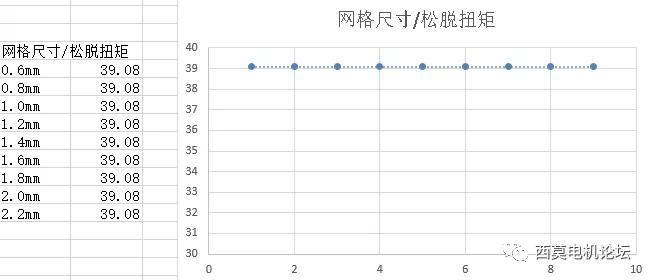
转速与松脱扭矩之间，呈线性下降趋势。

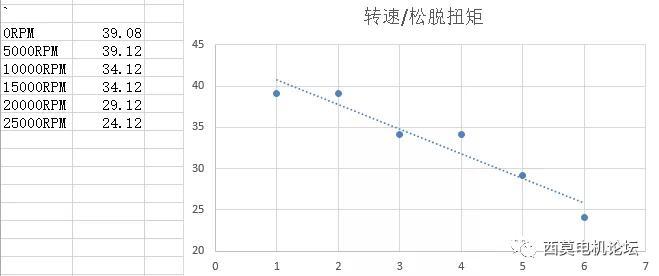
至此，本文仿真部分完成。

以上案例为考察不同影响因素，对极限松脱扭矩的结果。当计算最大轴向压装力时，可将扭矩载荷，更换为对硅钢片侧面，施加局部推力载荷。建议仿真前，仿真工程师需了解并熟悉相关压装工艺，而后对实际压装位置与工装尺寸进行建模计算。

结果提取时，与本文相同，接触状态随推力载荷的变化曲线及其突变崩溃点，为极限压装力。

无论哪种工况，无论手工计算抑或仿真分析，均应以实际压装实验数据，为基准进行调试。否则计算误差将极其恐怖，如偏离2000%，以至于毫无参考意义。

当经过足够数量的验证后，笔者在汽车驱动电机，强度性能开发实际工作中，可实现采用相同设置下，同一套产品最大、最小、中位数的实际压装力与仿真差异，均为5%左右。

4 总结

本文借助《机械设计手册》手工计算方法，大致计算了承担500N轴向载荷，且45mm轴向长度时，压装力约7吨。过盈量0.036mm~0.085mm。

而后单独采用10mm轴向厚度的转子模型，计算临界松脱扭矩为15N·m~65N·m，并验证过盈量、摩擦系数、网格尺寸、转速等，对松脱扭矩的影响。还简单介绍了轴向压装力的仿真方法。

行文还中间穿插，部分强度仿真工作方法与经验分享。