高速电机转子冲片的强度设计（六）——极限失效扭矩及最大压装力计算方法（上）

1 前言

电机转子冲片与转轴之间，一般采用平/花键及或过盈配合等方法连接。

其主要用于传递与承担，电磁扭矩产生的载荷，并通过转轴向外传输轴功。根据其常见失效模式，一般为平键的剪切断裂及或磨损等，以及过盈配合零件的互相滑动及松脱等。本文主要介绍后者。

极限松脱失效扭矩，一般为冲片与转轴，在最小过盈量工况下，随着扭矩载荷的逐渐增加，转子冲片内径与转轴外径间，过盈配合表面的接触压力，从一个较大值逐渐降低，直至降低到某一临界点后，进入快速变形突变状态时，对应的扭矩载荷值。其主要服务于设计参数。

当发生过盈配合松脱失效时，如无平键等辅助应对保护措施，电机一般将失去对外输出轴功的基本功能，为最高等级的功能失效事故。为防止此类事故发生，应在设计过盈参数时，经过充分的手工计算、仿真分析、类比计算、验证性实验测试、仿真与实验对标等工作。

本文上半部分，主要借助《机械设计手册-连接于紧固-过盈配合》中介绍的方法，进行简略的手工计算过盈参数；下半部分主要通过静力学有限元仿真分析方法，相对更详细更细致的，探究过盈配合的各种性能指标与极限范围，以及对比不同网格尺寸、摩擦系数、过盈量、转速等对极限松脱扭矩的影响关系。

转轴与硅钢片间过盈配合装配工艺，一般采用温差或者机械压入的方法，将本来存在尺寸干涉的零件贴合、变形，并连接在一起的方法。

与上文类似的，最大压装力工况为冲片与转轴，在最大过盈量下，通过外界逐渐增加轴向压力载荷，当其增大到某一临界点后，过盈配合的接触状态将发生突变。其主要服务于工艺参数。本文仿真部分，将主要介绍极限松脱扭矩的计算方法。

当采用仿真分析法，进行过盈装配参数计算时，不但可以考虑推力载荷的影响，也可以借助多载荷步技术，设定冲片或转轴的温度环境，用于模拟冷装或热装等工艺过程及方法。从而对实际运行条件与工况，进行更完整、全面、深入的对比计算，从而更好的了解并实现设计性能。

无论是失效扭矩还是压装力，均为过盈配合连接的某个极限工况点。当借助实验或仿真等方法，得到该工况点对应载荷后，方可用于较为准确的预测和设计需要的过盈范围以及装配工艺参数等。

对于电机常用结构而言，电机转子和铁芯冲片之间，一般常采用机械压入的方法；定子铁芯与机壳之间，常采用热胀法。当用户足够土豪时，也可采用冷缩法。

过盈配合的有限元仿真分析，必须引入一组摩擦接触，即依靠在转轴外表面与冲片内表面之间的接触单元，实现了力与位移的传递。其为一种典型的接触非线性仿真分析，同时也是一种路径相关（不同加载方式与顺序，将带来不同的计算结果）的分析内容。由于不能直接预判结果，其最终结果及载荷与反作用力的平衡关系，需要进行多次迭代计算进行试算，造成了计算量较大。

迭代计算时，一般收敛的计算结果，是相对可参考的，但无法确保一定正确。即所谓的充分不必要条件。其仍需要使用者进行多方判断，结果的正确性及可用度；而不收敛的结果，参考性相对稍差，但不代表一定不可用。即所谓必要不充分条件。

由于仿真分析中，尤其是过盈配合部分的具体设置参数，将对极限失效扭矩及或最大压装力等关键结果，造成显著的影响和差异。故较为完善的且符合实际的仿真设置，应从大量的验证性实验数据中获得。

实验能力建设与各种验证性实验数据的积累及合理运用，一般为不同供应商间，真实仿真水平与能力建设及研发质量提升的主要门槛与限制。这就是笔者常说的，限制仿真水平的主要门槛，是钱。

确定过盈参数时，一般先采用手工计算的方法，进行初步的试算。而后借助有限元分析的仿真或压装实验等方法，进行校对与参数设置对标。

相对而言，采用手工计算方法，可以较为简单快速的获得，主要的设计参数和性能。但是由于其公式经过了大幅度简化，一般对于采用了复杂减重孔的，不均匀径向及环向刚度的电机铁芯冲片而言，无法准确的适用及评定，又由于过盈配合的位置，往往深入零件内部被仅仅压紧，十分不利于基于应变片相关的应力实验测定，故采用仿真方法，并搭配压装力实验，是一种更为有效的方式。 

2 硅钢片与转轴过盈配合的手工计算方法

本节主要技能点：

借助《机械设计手册-连接与紧固》承担轴向载荷时，过盈配合手工计算方法。

我们知道，有限元静态应力分析，一般遵循如下弹性力学的基本假设：1、完全弹性；2、小变形；3、均匀性；4、连续性；5、各向同性；6、无初始应力等。即理想弹性体及微小变形等。其或多或少的，不太适用硅钢叠片材料及过盈配合工况，但可通过补充及完善其他条件，用于更详细的仿真分析。

还需注意的是，实际摩擦突变过程，为从相抵较大的静摩擦，变为相对较小的动摩擦过程。在ANSYS Workbench静力学模块中，默认设置为本案例所示的，动静摩擦系数相同。也可插入APDL命令，设置库伦摩擦模型，并调整动静摩擦的转换关系，为阶跃或线性变化或其他细节形式。

正因为动静摩擦系数转换时，存在一个反作用力的阶跃突变点。所以实际生活中，当车辆即使采用相同的刹车力度，减速至接近停止时，会出现先低头，后被悬挂系统的压缩反作用力，而抬头的晃动过程。

同样的，手工计算过盈配合参数时，也应遵循一些基本假设，其包括：

1 被连接件材料在弹性范围内，即被连接件的应力，低于其材料的屈服极限；

2 被连接件为两个等长厚壁圆筒，其结合面间的压强均匀分布；

3 包容件和被包容件，处于平面应力状态，即轴向应力为零。其应力分布规律，如下图所示。图中假设，结合面压强为P，包容件与被包容件切向应力为σt和σr；

4 材料弹性模量为常数；

5 计算的强度理论采用变形能理论（冯•米塞斯应力）。

计算时需要的主要参数包括：传递荷载、被连接件的材料属性、摩擦系数、尺寸和表面粗糙度等；

遵循以上基本假设后，下图为过盈配合零件间内应力的分布规律。

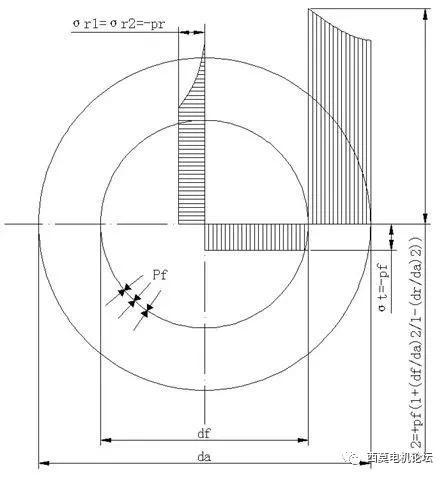
图-1 过盈接触面应力分布关系

由上图可以看出，实际模型的铁芯部分为空心，与机械设计手册中，公式的厚壁实心圆通的条件略有不同，故不能直接采用转子外径或中径等参数，带入手工计算公式。

考虑到本方案的铁芯过盈配合表面外圈，被极大程度的减重，其刚度明显低于实心圆柱，计算时需试探性的，将包容件的计算外径，用稍大于轴外径尺寸。

图上尺寸与某电机实际尺寸的对应关系如下：

d1=被包容件内径=0；

df=结合直径=54mm；

da=包容件外径=65mm（等效尺寸）；

p=结合面为ymax时结合面压强（不考虑装入压平的影响）；

T=转矩=78n•m；

lf=结合长度，总结合长度为90mm，但是转子采用两端斜级设计，装配时需分两次压装，故计算时采用的结合长度为90/2=45mm；

Fa=传递的轴力=500n（估计值）；

过盈配合连接设计的基本设计流程如下：

1 根据所需的传递荷载，确定最小结合面压强Pmin及相应的最小过盈量δmin；

2 根据已知被连接件的材料和尺寸，确定不产生塑性变形的最大结合面压强Pmax及相应的最大有效过盈量δmax；

3 根据最小过盈量δmin和最大有效过盈量δmax的计算结果，确定基本过盈量，再选出配合的最大过盈量【δmax】和最小过盈量【δmin】；

4 必要时再校核计算被连接件直径变化量；

5 计算过盈连接的装拆参数；

6 确定被连接件的合理结构和装配方法。

下面开始计算：

1 传递荷载所需的最小结合力压强

1.1 考虑传递转矩Pmin =2T/(π×df ^2×lf×μ)

其中T=78000n•mm、df=54mm、lf=45mm、u=0.15

结合面的摩擦系数µ根据下图查询。

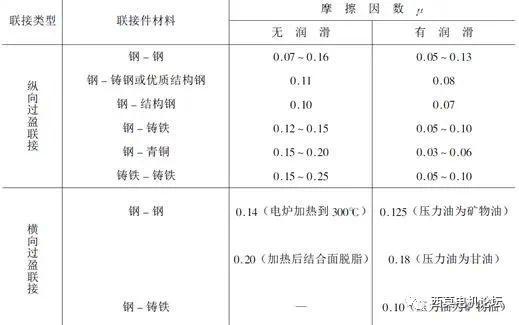
图-2 典型材料间摩擦系数

电机轴为纵向过盈配合连接、无润滑、钢对钢，查表得摩擦系数为0.07~0.16，故本手册取0.15；

将以上参数导入公式得

Pmin=2T/(π×df ^2×lf×μ)=2×78000/(3.1415×54^2×45×0.15)=2.523Mpa

1.2 考虑承受轴向力

Pmin=Fa/(π×df×lf×μ)=500/(3.1415×54×45×0.15)=0.437Mpa

取两者较大值作为Pmin

2、3 直径比

包容件qa=df/da =54/65=0.83077

被包容件，由于本转子为实心，故=0

4、5 传递荷载所需的最小直径变化量

4 包容件emin=Pmin×df×Ca/Ea =

其中Pmin=2.532Mpa、df=54mm、Ca=(1 qa^2)/(1-qa^2) νa、Ea查下图得碳素钢，为200Gpa，泊松比νa为0.3、qa=0. 83077

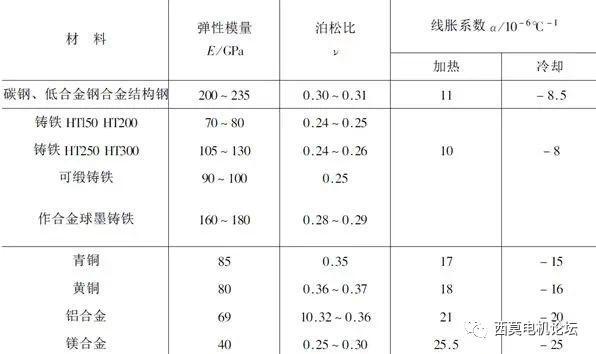
图-3 典型材料的物理参数

将以上参数带入公式得

Ca=(1 qa^2)/(1-qa^2) νa=（1 0.83077²/1-0.83077²） 0.3=5.755

emin=Pmin×df×Ca/Ea =2.532×54×5.755/200000=0.003934mm

5 被包容件公式与上文类似，其中qa=0

所以Ca=(1 qa^2)/(1-qa^2 ) νa=（1 0/1-0） 0.3=1.3

emin= Pmin×df×Ca/Ea =2.532×54×1.3/200000=0.0008888mm

6 传递荷载所需的最小有效过盈量

δmin=0.0008888 0.003934=0.004823mm

7 考虑压平量所需的最小过盈量

δmin=δmin 2（Sa Si）=δmin 2（1.6Ra 1.6Ri）

其中Ra为轮廓算数平均偏差，假设为0.001mm

带入公式得0.004823 2（1.6×0.001 1.6×0.001）=0.01122mm

8、9、10不产生塑性变形所允许的最大结合压力

8 包容件p=a·σa

其中a=(1-qa^2)/√(3 qa^4 )

其中qa=0.83077、σa=420Mpa

带入公式得1-0.83077²/（3 0.83077⁴）^0.5=0.1662

p=420×0.1662=69.7Mpa

9 被包容件p=c·σa

其中c=(1-qi^2)/2

qi=0，则c=0.5、而σa=1100Mpa

带入公式=550Mpa

10 被连接件p取以上两者（550Mpa和69.7Mpa）较小者，则=69.7Mpa

11 被连接件不产生塑性变形的传递力

Ft=p·π·df·lf·µ=69.7×3.1415×54×45×0.15=79814N

12、13 不产生塑性变形所允许的最大直径变化量

12 包容件e=p·df（Ca/Ea）=69.7×54×5.755/200000=0.1083mm

13 被包容件e=p·df（Ca/Ea）=69.7×54×1.3/200000=0.0245mm

14 被连接件不产生塑性变形所允许的最大有效过盈量

δ2=0.1083 0.0245=0.1328mm

配合选择

15 初选基本过盈量

δ=(δmin δ2)/2=（0.01122 0.1328）/2=0.072mm

16 确定基本偏差代号

根据δ=0.072mm和df=54mm查阅下图。

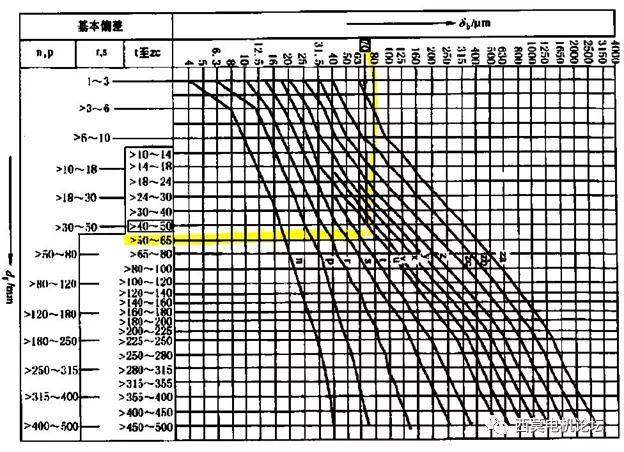
图-4 配合代号查询

查阅上图得配合偏差代号为t。则查询下图可知，过盈配合可选T7/h6。

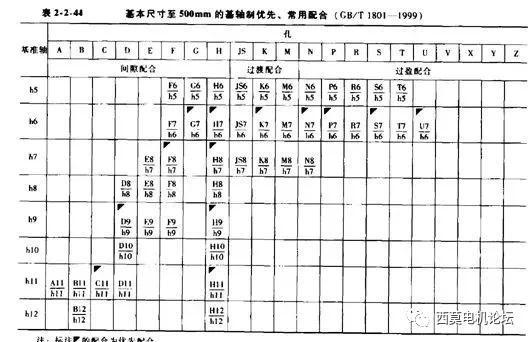
图-5 配合公差查询

根据配合参数参考下图可知，直径54mm电机轴的优选过盈量为0.036~0.085mm

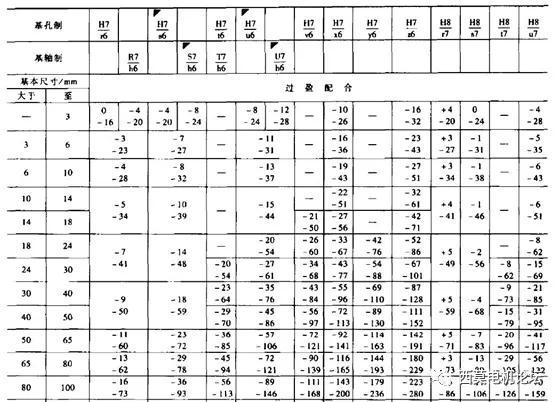
图-6 配合尺寸查询

校核计算与被连接件直径变化量略。

过盈连接的装配参数

17 采用压入法时，需要的压入力

p=p·π·df·lf·µ=69.7×3.1415×54×45×0.15=79814N

根据某电机转子尺寸等参数，在需要承担78N•m扭矩和500N轴向力荷载下，计算结果如下：

1 过盈配合最小接触压力为2.532Mpa，不产生塑性变形所允许的最大结合压力69.7Mpa；

2 考虑压平量的最小过盈量为0.072mm，被连接件不产生塑性变形，所允许的最大有效过盈量0.1328mm；

3 采用压入法时，每一级转子铁芯，需要的压入力为79814N；

4 根据配合尺寸，优选过盈量为0.036mm~0.085mm。

至此，本节上半部分完成，下面介绍仿真分析部分。（未完待续）