结构振动加速度分析的来龙去脉
在做楼盖竖向振动舒适度分析的时候,我们经常要计算振动加速度。算的案例多了,就会发现,加速度计算,多数情况下,其实是一笔糊涂账。
概况来看,三方面因素导致加速度计算结果存在较大的离散性:1)模型处理层面:结构边界条件、材料弹性模量取值、梁的刚度放大系数、梁与板是否顶平等;2)荷载与激励:荷载取值、人行激励的加载点、加载数量(单人or多人)、加载方式(是否考虑随机性)、人行激励频率取值等;3)结果判别方面:加速度是看瞬态结果,还是稳态结果。
上面提到的问题,今天都不讨论。如果对这些问题感兴趣,可以翻看本号的一篇旧文《楼盖舒适度判别的深度解析》。
今天,我们讨论一个最简单的单自由度结构的振动问题。
1、振动频率为3.0Hz的单自由度结构
首先,构造一个单自由度结构。一根跨度为6m,截面为250mmX250mm的混凝土简支梁,材料为C30;梁跨中作用一个集中力,大小为59.592kN,梁只提供刚度,集中力提供质量,该单自由度结构竖向振动频率为3HZ。
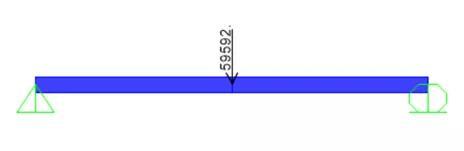
图1 单自由度结构
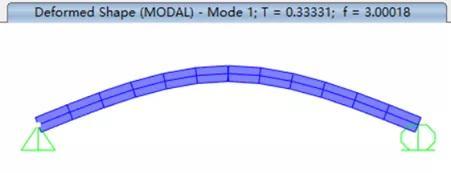
图2 竖向振动频率3.0Hz
2、单自由度结构-余弦激励
我们在梁跨中作用一个余弦时程。
F(t)=0.35cos(2π·3t)
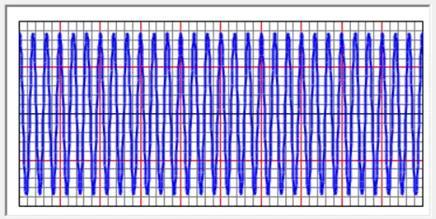
图3 简谐时程激励
分析得到激励点的振动加速度时程曲线如下, 最大加速度为0.574m/s2.
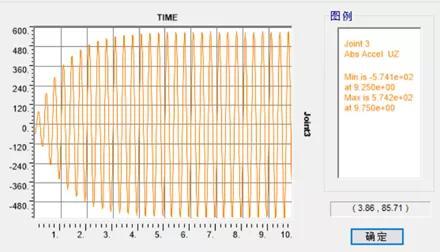
图4 振动加速度时程曲线
2.1 单自由度的时域分析
上述单自由度的简谐振动问题,我们求解的其实是强迫振动的加速度幅值。
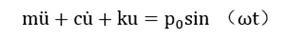
强迫振动的位移时程可以表达如下:
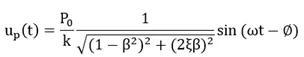
动力幅值等于静力位移(ust)乘以动力放大系数(Rd),当共振时,即beta=1.0,阻尼比定为5%, 则Rd=10.
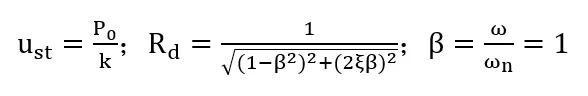
按上述公式计算位移幅值:
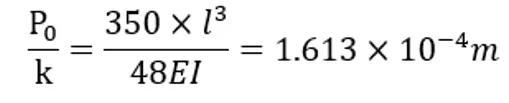
位移动力放大系数Rd=10,加速度在位移的基础上二次求导,放大系数为(6π)^2,最终我们计算得到加速度幅值为1.613e-4x10x(6π)^2=0.573m/s2,与SAP2000计算结果(0.574m/s2)一致。
2.2 单自由度的稳态分析
SAP2000也提供了稳态算法。根据激励时程,我们在频率3.0HZ附近定义一个稳态函数,然后按稳态分析计算激励点的加速度幅值。
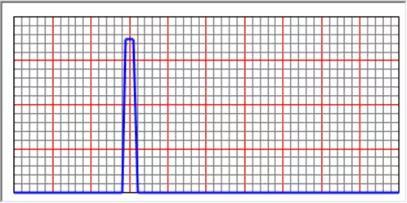
图5 稳态函数
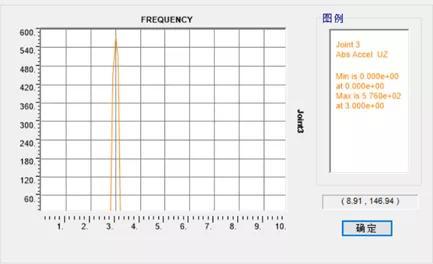
图6 稳态分析得到的加速度副值
根据稳态分析得到的加速度幅值为0.576m/s2,与时程分析基本一致。
2.3 单自由度的频域分析
有意思的是,SAP2000 V21版在时程分析时,除了常规的模态法和直接积分法,还给出了频域法。频域法得到的计算结果为0.5758m/s2。
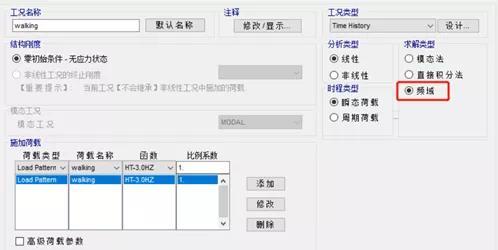
图7 弹性时程求解类型的频域法
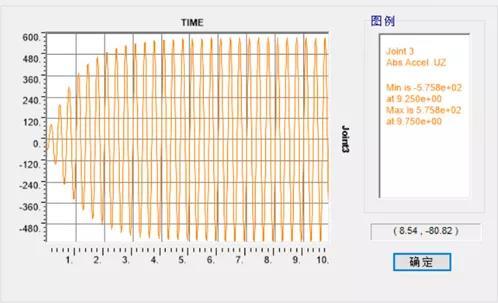
图8 加速度时程曲线-频域法
对单自由度简谐振动,频域解也不难得到。
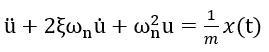
首先将荷载在其频域上展开:
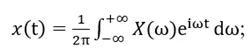
则总响应为:
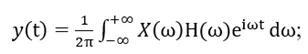
将y(t)用傅里叶转换来表示:
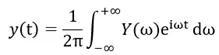
最后,我们得到一个频率上的转换关系
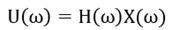
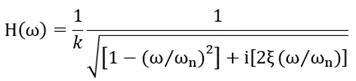
当发生共振,阻尼比取5%时,加速度幅值关系为:
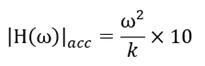
同样地,与时域分析法类似,可以得到加速度幅值为0.573m/s2.
根据上述推导,我们不难理解SAP2000弹性时程中频域分析法的基本步骤:
1)对外荷载x(t)做傅里叶变换,得到荷载的傅里叶谱X(w);
2)根据外荷载傅里叶谱X(w)和复频响应函数H(w),得到结构反应的频域解U(w);
3)应用傅里叶逆变换,由频域解U(w)得到时域解u(t).
理论上,频域分析法与直接积分的时域法等效。
2.4 结论
1)针对单自由度的余弦激励时程,我们采用时域分析、稳态分析、频域分析,并结合手算,均得到基本一致的加速度幅值。
2)加速度幅值大小与结构的静态位移、荷载角频率、结构阻尼比相关,当结构发生共振,结构阻尼比取5%,则加速度幅值为:

所以你看,结构共振,相当于一个动力放大器,它将静态位移放大10倍,将静态加速度也放大10倍。如果阻尼比为2%,则放大系数为25倍。
3)在上面的案例中,激励时程峰值仅相当于单自由度质量的0.587%,即使阻尼比为5%,得到的加速度幅值为0.576m/s2,远大于规范限值。
3、单自由度结构-人行激励
接下来,我们将荷载替换为人行激励,行走激励荷载函数参考《建筑楼盖结构振动舒适度技术标准》5.2.1条,但激励频率取为1.5Hz
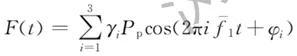
按照上述公式,得到的激励时程如下所示:
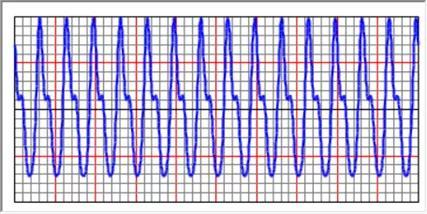
图9 人行激励时程
然后我们分别按三种方法计算加速度幅值。
3.1 时域分析
加速度幅值为0.253m/s2;
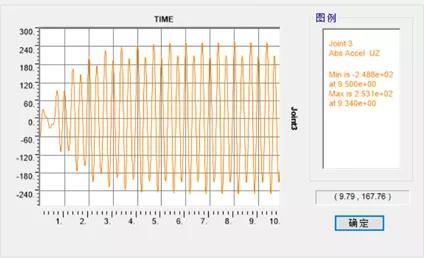
图10 时域分析加速度时程
3.2 稳态分析
先定义稳态函数,然后得到三个频率点的加速度幅值分别为0.021m/s2、0.230m/s2、0.021m/s2。
手算加速度幅值与SAP2000计算结果基本一致。
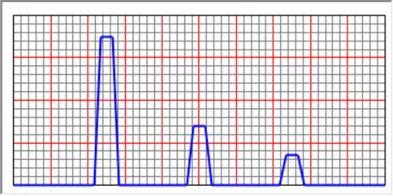
图11 稳态函数
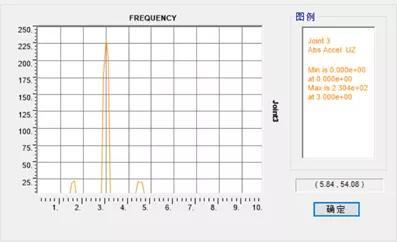
图12 稳态函数计算的加速度幅值
从激励函数来看,函数后两阶相位一致,与函数第一阶相位相差π/2,将三个频率点加速度幅值进行组合,sqrt(0.021^2 (0.230 0.021)^2)=0.2519m/s2.
3.3 频域分析
时程分析类型选择频域法,得到的加速度幅值为0.2529m/s2。
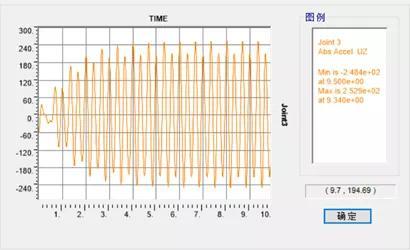
图13 频率分析得到的加速度时程
上述三种分析方法,得到的加速度幅值基本一致。
3.4 结论及人行激励取值讨论
1)在上述案例中,人行激励函数第二阶频率与结构自振频率相同,因此在第二阶频率得到最大的加速度幅值。虽然荷载幅值仅为第一阶函数的40%,但加速度幅值为第一阶的11倍。
2)进一步,我们将结构频率调整为4.5Hz,此时,激励第三阶频率将与结构发生共振。此时,各激励频率点的加速度幅值如下图,前三阶加速度幅值为1:2.8:16.3。
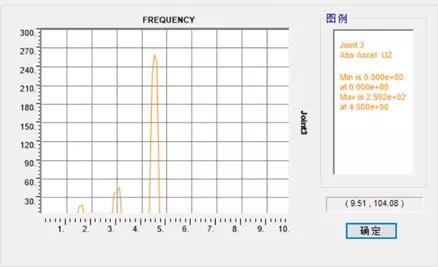
图14 结构频率4.5Hz-稳态分析
3)根据上述两条讨论,选择人行激励函数时,激励函数频率点应尽量包含结构自振频率点。最优选择为荷载第一阶频率与结构共振,其次为第二阶频率与结构共振,再次为第三阶频率与结构共振。
4)舒适度技术标准对人行激励频率点的取值,建议如图15所示。这条规定让不少工程师困惑,如果结合本文的讨论,我们将很容易理解该规定的含义。

图15 激励频率取值-舒适度技术标准
比如结构振动频率为3.6Hz,荷载频率首先应该选择1.8Hz;结构振动频率为6.0Hz,荷载频率首先应该选择2.0Hz。
5)根据舒适度技术标准,人行激励频率范围为1.6~2.2Hz,则结构自振频率在1.6~2.2Hz,3.2~4.4Hz,4.8~6.6Hz时,我们均可以找到一个可以共振的激励频率。
6)如果结构自振频率没有落在上述三个频率范围呢?比如2.8Hz,2.8/2=1.4<1.6,应该取1.6Hz;同时2.8/1=2.8>2.2,也应该取2.2Hz,究竟是1.6Hz计算出来的加速度更大,还是2.2Hz更大呢?
对单自由度结构,我们知道加速度幅值为:
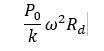
Rd与关系如下图所示:
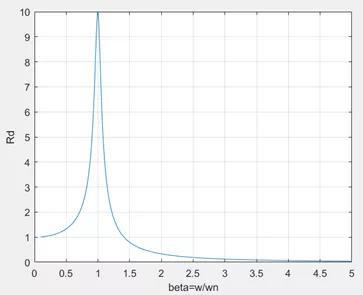
图16 频率比与Rd关系曲线
手算复核,这两条激励(1.6Hz和2.2Hz)计算的加速度幅值非常接近,在不好把握的情况下,建议这两条激励均进行计算。
接下来,我们会继续对此问题进行深入研究。
JIE 构生活,是以一名结构工程师的视角,分享他在结构设计、咨询,学习以及生活等方面的见闻及思考。旨在吸引更多志同道合的朋友共同进步。





