发表160多年的圣维南原理,为何没人用理论推导出来?
本文摘要(由AI生成):
文章主要介绍了圣维南原理,包括其定义、适用范围、局限性以及工程实践应用。圣维南原理是一种针对物体力的边界问题的解决方法,它解决了平面问题的微分方程的复杂的小边界的力的边界条件问题。圣维南原理只适用于小边界或次要边界,要求边界上的应力的合力与原面力静力等效。文章通过模拟示例,展示了圣维南原理在工程实践中的应用,并提出了三个问题:长度要求远远大于宽度的最小值、理论发表至今一百六十多年为啥没有人用理论推导出来、圣维南原理到底靠谱不。
圣维南原理到底靠谱不?众所周知,圣维南1855年发表了关于柱体扭转和弯曲的论文,并提出了局部效应原理(即圣维南原理)。这个猜想并没有被理论证实,但是却被工程实践所接受,一直延续至今。
那么到底什么是圣维南原理?
圣维南原理表明:如果把物体的一小部分边界上的面力,变换为分布不同但静力等效的面力(主矢量相同,对于同一点的主矩也相同),那么近处的应力分布将有显著的改变,但是远处所受的影响可以不计。
把以上内容翻译一下就是:针对物体的力的边界问题,如图一,作用于杆件两端轴线上的拉力F,假设L>>A(其中L为杆件长度,A为杆件宽度),那么当对拉力F进行静力等效时,那么有显著影响的区域只是在虚线内侧,而对虚线外侧几乎没有影响,在工程上可以忽略不计。

图一
圣维南原理的提出,解决了平面问题的微分方程的复杂的小边界的力的边界条件问题,值得注意的两点是:
1、圣维南原理只适用于小边界,或次要边界
2、要求边界上的应力的合力与原面力静力等效
综上所述:圣维南原理只适用于左右两侧的小边界,而不适用上下两侧的大边界。左右两侧的节点静力F可以等效为两个节点力F/2或者等效为面力F。
对图一进行模拟示例:模型长度L=500mm,宽度和厚度为10mm,左端固定,右端施加力100N,材料为结构钢。
(1)根据材料力学中的公式σ=F/A=100N/10^2mm2=1MPa,因此,应力值应为1MPa。
(2)用ANSYS19.0对图一各个工况进行模拟,左端固定约束,采用20节点Solid186单元,共计节点数量3021,单元数量400。
工况一:右侧中心施加节点力F=100N


工况二:右侧对称两个节点施加节点力F=100N
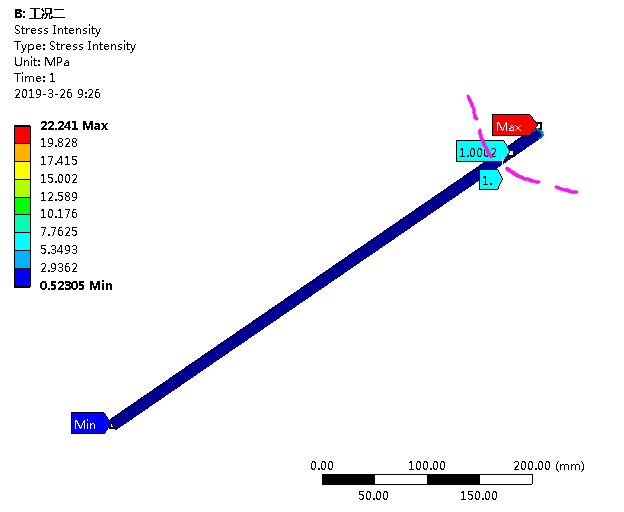

工况三:右侧施加面力F


通过三个工况的模拟,影响区域为虚线标记的部位,跟图一所示基本相同,但是根据力的等效的不同,所影响的区域大小以及应力强度最大值也有所不同,也就是说圣维南原理只是一个粗略的等效假设。
那么问题来了:
问题1,长度要求远远大于宽度,这个远远大于的最小值是多少?
问题2,这个理论发表至今一百六十多年为啥没有人用理论推导出来?
问题3,圣维南原理到底靠谱不?
作者简介:孙捷飞,A1、A2、C2、C3级压力容器审核员,从事低温深冷压力容器以及移动式压力容器设计审核工作。
声明:首发贤集论坛,如需转载请联系我,禁止私自转载。




