一、时域分析
齿轮箱振动信号的时域和频域分析
来源:内容整理自百度文库,由用户锅铲貂肆于2013年4月16分享。
在各种齿轮箱故障分析与诊断方法中,以振动检测为基础的齿轮箱故障诊断方法具有测量简便、实时性强等优点,通过测量齿轮箱运行过程中所产生的振动信号,作为故障诊断的重要信息来源,是一种理想的齿轮箱运行监测工具。目前研究和应用的振动检测与故障诊断的方法可以分为以时域分析和频域分析两种。
时域分析方法就是根据信号的时间历程记录波形,分析信号的组成和特征量。对于离散的时序数据,常用的有量纲幅域参数有:峰值、均值和均方根值。
峰值:
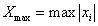
均值:
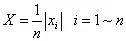
均方根值:
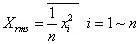
均值和均方根值都是描述动态信号强度的指标。幅值的平方具有能量的含义,因此均值表示了单位时间内的平均功率。
无量纲幅域参数有:峰值指标、裕度指标和峭度指标。
峰值指标:
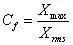
裕度指标:
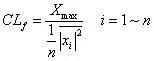
峭度指标:
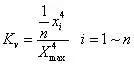
峰值指标表示信号的变化范围,是信号强度的一种描述;裕度和峭度对信号的冲击较敏感,可以用作齿轮箱的故障诊断,如因齿轮裂纹、滚动轴承故障等在时域波形中就可能引起相当大的脉冲。
二、频域分析
工程上所测得的信号一般为时域信号,然而由于故障的发生、发展往往会引起信号频率结构的变化,为了通过所测信号来了解、观测对象的动态行为,往往需要频域信息。将时域信号变换至频域加以分析的方法称为频域分析。其目的就是把复杂的时间历程波形,经傅立叶变换分解为若干单一的谐波分量来研究,以获得信号的频率结构以及各谐波幅值和相位信息。常用的频域分析包括频谱分析、细化谱分析和解调谱分析等。
1. 频谱分析
频谱分析中常用的是自功率谱。自功率谱的定义如下。
将时域信号x(t) 进行傅里叶变换的:
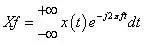
其自功率谱为:
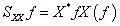
式中,X*f 是X(f ) 的共轭复数。
自功率谱亦可以从自相关函数进行傅里叶积分得到。
2. 细化谱分析
细化分析技术是近年来由FFT方法发展起来的一项新技术,是一种用以增加频谱中某些有限部分上的分辨能力的方法,即“局部放大”的方法,可使某些感兴趣的重点频段得到较高的分辨率。细化分析方法很多,比如Chirp. Z变换、Yip—Zoom变换及相位补偿Zoom—FFT等等,而现在应用比较广的是复调制细化方法以及它的改进算法。
3. 解调谱分析
在实际齿轮箱系统中,复杂的幅值调制与频率调制是同时存在的,频谱上出现不同程度的调制边带。在工程实际中常用复包络分析方法及其改进算法来对齿轮箱的振动信号进行解调分析。复包络分析方法是利用希尔伯特 (Hilbert) 变换对齿轮啮合振动信号解调而获得调幅和调相信号,然后求出调幅和调相信号的频谱图,再根据频谱确定齿轮箱故障。




