球坐标系下的弹性力学问题
来源:力学酒吧(ID:Mechanics-Bar),作者:张伟伟。
球坐标也被称为“空间极坐标”。在(平面)极坐标系内,一点的位置有两个坐标变量 (ρ,φ),φ 表示称为极角,用来确定一点的方位角;ρ 为极径,表示该点离开坐标原点的距离来确定点的位置。球坐标与此十分类似,只是表达方位时多了一个坐标变量,如一点的坐标表示为 (r,θ,φ),其中θ、φ 表达一点在空间的方位,θ 为天顶角,表示该点与原点的连线(径向连线)与z 轴的夹角,如图1(a)所示,φ 表示径向连线在xoy 平面内的投影与x 轴的夹角,称为方位角,r 相当于坐标中的ρ,仍然表示该点在离开坐标原点的距离(径向距离)。
需要特别注意的是,不同的文献采用球坐标时,θ、φ 的意义可能并不完全相同,在图1(a)所示的球坐标之外还有图1(b)所示的球坐标,它们的θ、φ 意义正好相反,但描述一点的坐标都是(r,θ,φ),这是需要特别注意天顶角和方位角的选取。
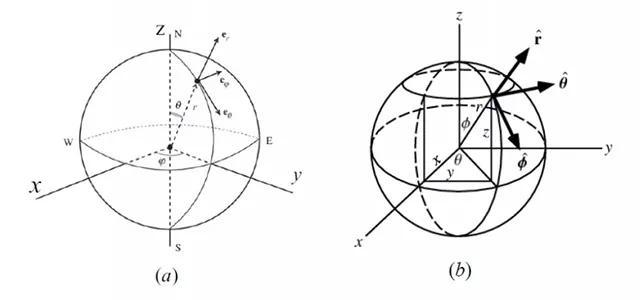
图1 球坐标的两个表达
在徐芝纶《弹性力学》(第5版)中,球坐标用于处理球对称问题,由于对称性,θ 方向和φ 等价,两个方向的应力、应变都用σT、εT 表示,回避了采用哪类极坐标的问题。吴家龙《弹性力学》中清晰地给出了图1(a)所示的球坐标系,一般情况下,在物理、力学中,图1(a)所示的球坐标使用的广泛一些,在数学类的教材中,使用图1(b)球坐标的情形多一些。因此,在力学中默认选用的图1(a)所示的坐标系。
在工程中,有许多球对称问题,例如图2(a)所示球形储气罐,以及图2(b)所示的球形爆炸容器(防爆球),这类结构通常在高压条件下工作,为了确保使用安全性,求解球形容器在工作条件下的应力、应变就显得异常重要。由于研究对象为球形,在几何形体上满足球对称,即过球心的任意平面都是该几何形体的对称平面,这也被视为关于球心(点)对称,球体绕球心在空间任意旋转后,仍与初始状态重合。
当满足球对称的几何结构,约束和载荷也为球对称时,这类弹性力学问题被称为球对称弹性力学问题,其应力、应变和形变位移也是球对称的,十分适合采用球坐标,同时边界和边界条件采用球坐标来描述也可以得到极大的简化。以下我们分别来推导球对称弹性力学问题的基本方程和边界条件。

图2 球形容器
在不考虑刚体 位移时,球面上任意一点的位移只能有径向(r 向)位移uρ,而没有切向(θ 和φ 向)位移,即uφ≡uθ≡0,同时由于θ、φ 方向位移等价,也将它们统一记为uT≡0。可见,球对称问题只需要考虑一个位移分量ur。
现在来考虑应变分量,设在球体上任取一点P,并以该点为基准,分别沿r、θ、φ方向做增量dr、ρdθ (∠POB=dθ)、ρdφ (∠POC=dφ),如图3所示。
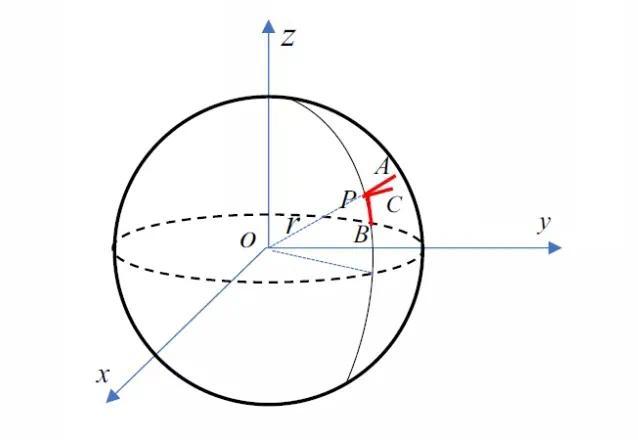
图3 球面上P-ABC构型
为了更清晰的分析构型P-ABC的变形,分别画出该构型分别在rθ、rφ、θφ 三坐标平面内的投影,如图4所示。
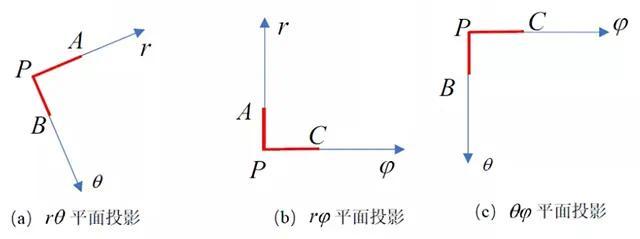
图4 构型P-ABC在三个坐标平面上的投影
首先,以图4(a)所示视角观察,当P、A、B三点只有r 向位移时,设P点位移为ur,利用泰勒级数展开,保留一阶导数得A 点位移为ur (əur/ər)dr,写出r 方向的应变为
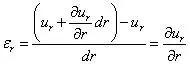
因P点和B点在φ 方向位移均为0,可不考虑。但是因P点和B点同为球面上的点,当球面膨胀或缩小后,PB在变形前后球面上的距离发生改变,引起θ 方向的应变,由于P、B 在r 方向的位移为ur,(不相等时会破坏球对称),可知变形后PB长为(r ur)dθ,因此有
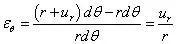
再来考虑PA和PB夹角的改变,因P、A只在r 向发生位移,不会发生偏转,同时由于P、B在r 方向的位移为ur(不相等时会破坏球对称),也不会发生偏转,因此
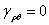
再以图4(b)视角观察,对PA变形等同于图4(a)视角观察结果,得下式所示结果
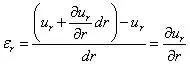
对PC的变形分析,等于图4(a)视角中对PB的观察结果,只是方向被切换至φ 方向,有
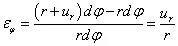
可见,εθ=εφ=ur/r,因此统一将θ、φ 方向的线应变记为εT。同理,考虑PA与PC夹角的改变,因PA与PC均不发生偏转,所以
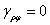
最后,以图4(b)视角观察,因球对称各点在θ、φ 方向没有位移,因此在θφ 平面内观察构型P-ABC,在变形前后保持不变(各点只有垂直于θφ平面的位移),PB和PC的应变分量如(b)和(c)所示,其切应变为0。
整理三个视角的结果,并考虑到应变只是r 一个变量的函数,偏导可以写为导数,有
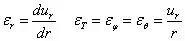
此即为球对称问题的几何方程。可见,球对称问题只需要考虑三个应变分量,将θ、φ 方向应变等价考虑后,只需要考虑两个应变分量,其它应变分量均为0。将应变分量代入物理方程(广义胡克定律),有
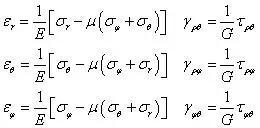
因切应变全部为0,可导出τρθ=τρφ=τφθ=0。利用线应变的三项,写出用应变表示应力的物理方程,有
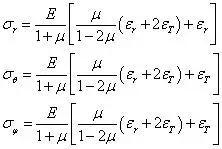
可见,σθ=σφ,也将σθ 和σφ 统一写为切向应力σT。将其整理后,写为
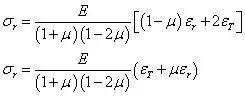
最后来建立平衡方程,取图5所示微元体。注意一点,由于球对称问题的应力只是半径r 的函数,因此应力对坐标的偏导,可以写为导数。
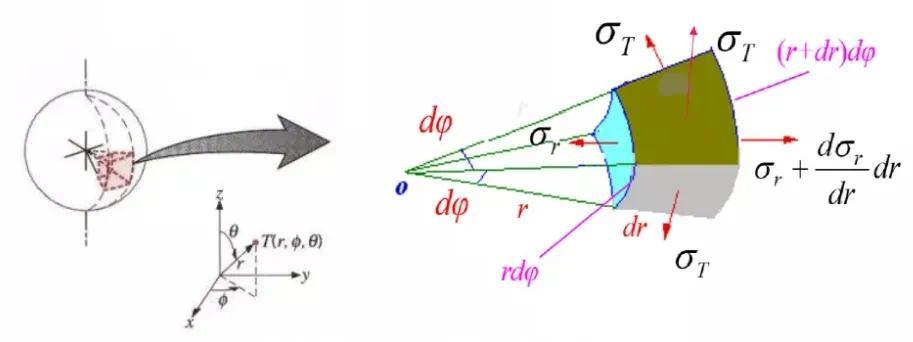
图5 球对称问题列平衡方程的微元体模型
因此,r 方向的平衡方程,有
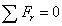
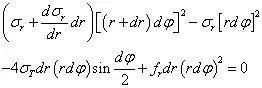
考虑到,当dφ 很小时,sin(dφ/2)≈dφ/2,同时,将两边同除以r²drdφ²,再略去高阶无穷小,有
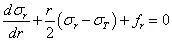
由于在θ 和φ 方向应力不发生变化,自然平衡,可不予考虑。由此可见,球对称问题的平衡方程只需要写r 方向的平衡,只有一个方程。整理一下,球对称问题平衡方程有1个,几何方程2个,物理方程2个,共5个方程;未知量包含位移分量ur,应变分量εr、εT,应力分量σr、σT,共5个未知量。
如果我们回顾一下坐标系的学习历程,对于平面问题,从平面直角坐标系到极坐标,虽然都是8个方程求解8个未知量,但由于边界条件的特殊性,能用极坐标求解的问题就显得比直角坐标系的问题简单。对于空间问题,空间直角坐标系需要利用15个方程求解15个未知量,柱坐标求解的空间轴对称问题,是利用10个方程求解10个未知量,再到球坐标求解的球对称问题,则是用5个方程求解5个未知量。
从问题的难度来看,直角坐标系直观性强、理论便于理解,非直角坐标系相对抽象、理论推导略显复杂。但从它们求解的题目来看,非直角坐标系比直角坐标系下的题目大大简化,特别是球坐标解决的球对称问题,由于所有的未知量只是半径的函数,偏微分方程变成了常微分方程,使得问题的求解得到了较大的简化。换言之,我们先学直角坐标系,一开始就把弹性力学中最难求解的题目学了,然后再学别的坐标系,题目求解难度都在降低。
对于球对称问题,边界条件的描述也十分简单,如应力边界条件的公式如下,
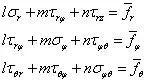
考虑一空心球体,在外球面上,法线与半径方向(r 方向)相同,与θ、φ 垂直,因此,l=1,m=n=0。由于球对称,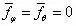 。因此上式变为
。因此上式变为
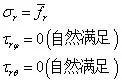
只需要考虑r 方向的面力与应力平衡即可,边界上3个式子变为1个。位移边界条件,也因球对称,只需要考虑r 方向的位移约束,写成
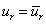
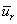 表示球面上的已知位移。
表示球面上的已知位移。
参考资料:
徐芝纶. 《弹性力学》(第五版)2016
吴家龙《弹性力学》2001




