柱坐标系下的弹性力学问题
来源：力学酒吧，作者：张伟伟
柱坐标是在极坐标的基础上发展起来的，相当于地将极坐标面向z方向拓展，在极坐标里确定一点的位置坐标为 (ρ,ψ)，在柱坐标里则为(ρ,ψ,z)。
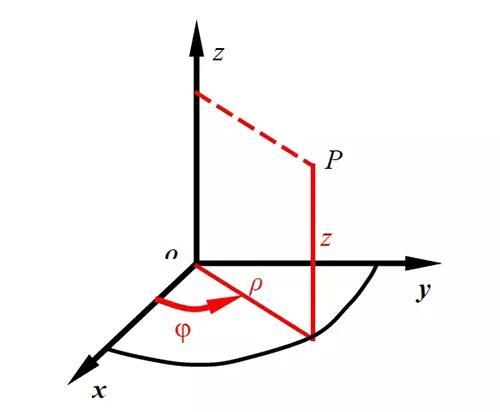
图1 柱坐标示意图
我们知道，极坐标在处理圆形、扇形、楔形等平面问题时具有显著的优势。当弹性体具有空间轴对称性时，采用柱坐标将会带来极大的方便性。所谓空间轴对称问题，则弹性体关于通过对称轴的任意平面都对称。此外，轴对称也是绕轴对称，过对称轴做任意平面与空间几何体相交，产生的形状都相同。常见的空间轴对称结构如圆柱体、圆台、圆锥和椭球体等。
图2 工程上的各类轴对称结构举例
空间轴对称弹性力学问题，除了要求弹性体几何上具有轴对称性，还必须要求其所受的载荷和约束也是轴对称的。举例而言，混凝土浇筑管道，在其外表面360°受相同的位移约束，为轴对称约束；当管道内受均匀内压时，其载荷也为轴对称。此时，求解管道的应力、应变、位移，该问题可简化为轴对称问题，且应力、应变、形变位移也应该具有空间轴对称性。
图3 混凝土浇筑管道其约束和载荷轴对称示意图
以下分别讨论空间轴对称问题的基本方程，以及其边界条件。我们先分析空间轴对称问题的形变位移。
对于空间轴对称问题，因为弹性体的几何结构、载荷、约束均为轴对称，其变形也必然为轴对称，设uρ、uφ、w 是弹性体的形变位移分量，则可以导出uφ≡0。如图4所示，设p 和p' 的位移绕z 轴对称，旋转任意角度后位移分量都相同，考虑绕轴对称，从P 点旋转到p'点，其环向位移方向如图中实线所示。另一方面，轴对称问题过对称轴的任意平面都是对称平面，因此p 和p' 的位移又关于y 轴对称，p' 点的环向位移为图中虚线所示。由于p' 不能同时向两个相反方向运动，所以p' 点的位移只能为0，即uφ≡0。
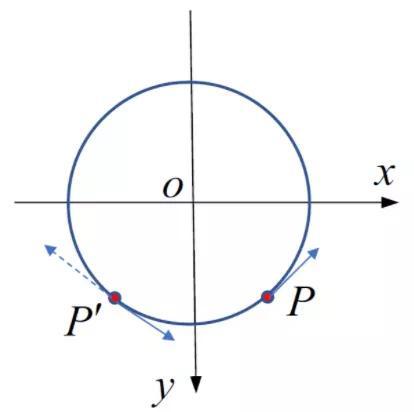
图4 轴对称图形上点的环向位移
可见轴对称问题位移分量uφ 与φ 的取值无关，同理也可以证明轴对称问题uρ（ρ 方向的位移）和w（z 方向的位移）也与φ 无关，它们只是 (ρ, z) 的函数，具有相同z 坐标和ρ 坐标的点，其uρ 和w 均相同。
现在我们来考虑柱坐标系下弹性体的变形问题，推导坐标系下的几何方程。参考图5所示的构型P-ABC，设PA=dρ，PB=ρdφ，PC=dz。以下分别考虑ρ 和z 两方向位移产生的应变分量，然后叠加得到总的应变分量。
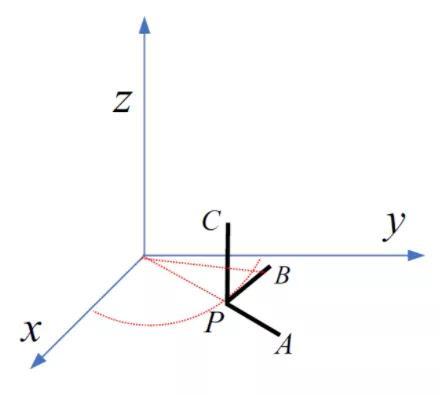
图5 推导几何方程的空间构型
(1) 只有径向（ρ 方向）位移时
PB变形前长ρdφ，变形后长 (ρ uρ)dφ（设径向位移量为uρ），因此
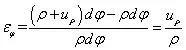
对于PA，设P点位移uρ，则A点位移uρ (əuρ/əρ)dρ，因此
对于PC，设P点位移uρ，则C点位移uρ (əuρ/əz)dz，因此PC变形后的长度为√dz² (əuρ/əz)²，考虑小变形假设，有əuρ/əz<<dz，因此，PC变形后的长度近等于原长，因此εz=0。
考察∠APB的改变量，由于只有径向位移，PA不发生偏转。从P点到B点，只是φ 坐标增加dφ，因此P点和B点方向位移相等，因此PB也不发生偏转。所以γρφ=0。
考察∠BPC的改变量，由于P点和B点在ρ 方向位移相等，变形前后PB都垂直于面PAC，而PC只在面PAC中变形，因此PB变形前后都垂直于PC。所以γzφ=0。
考察∠APC的改变量，因为P点位移uρ，则C点位移uρ (əuρ/əz)dz，因此PC将发生偏转，同时也是γzρ 的取值为
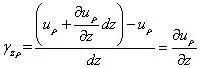
(2) 只有轴向（z方向）位移时
对于PA和PB，变形后它们可能略有倾斜，由于小变形假设，倾斜量很小，它们变形后的长度近似等于变形前的长度（类似于只考虑径向位移时，PC的变化），因此有ερ=0，εφ=0。
对于PC，设P点位移为w，则C点位移为w (əw/əz)dz，因此
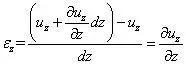
考察∠APB的改变量，考虑对称性，P点和B点在z方向的位移相等，当只有z方向位移时，PB始终垂直于面PAC，因此，γρφ=0。
考察∠BPC的改变量，只有z方向位移时，PC不发生偏转，PA可能发生偏转。设P点位移为w，则A点位移为w (əw/əρ)dρ，因此
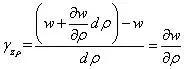
(3) 叠加
当同时存在径向位移和轴向位移时，叠加上述两种情况下的应变分量，得到空间轴对称问题总的几何方程，为
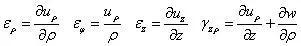
γzφ≡0，γρφ≡0，求解空间轴对称问题时，可以不予考虑。
上式所示，即为空间轴对称问题的几何方程，可以看出对于空间轴对称问题，只需要考虑4个应变分量。现在考虑广义胡克定律，有
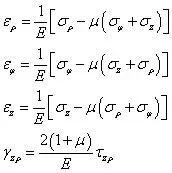
由于γzφ≡0，γρφ≡0。可以导出τzφ=0和τρφ=0。因此，广义胡克定律只有4个方程。将上式中前三项相加，得
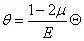
θ 称为体积应变，有θ=ερ εφ εz，Θ 称为体积应力，有Θ=σρ σφ σz。将广义胡克定律写成以应变表示应力的形式为
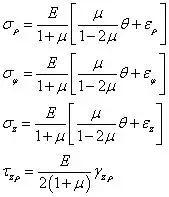
从上式可以更清楚的看到，空间轴对称问题只需要考虑4个应力分量，减少了2个应力分量，使问题得到简化。
考虑空间轴对称问题，取如图6(a)所示的微元体，该微元体由两个柱面以及两个通过对称轴的平面组成，高度为dz，两个柱面之间的距离为dρ，两个过对称轴的平面所成角度为dφ。以P点为基准点，写出各面上的应力分量，PAB面上为σz、τzρ，PAC面上为σφ，PBC面上为σρ、τρz，利用泰勒级数展开式，只保留一阶导数项，可写出微元体各相对面上的应力分量，同时考虑体力fρ 和fz，如图6(b)和6(c)所示。
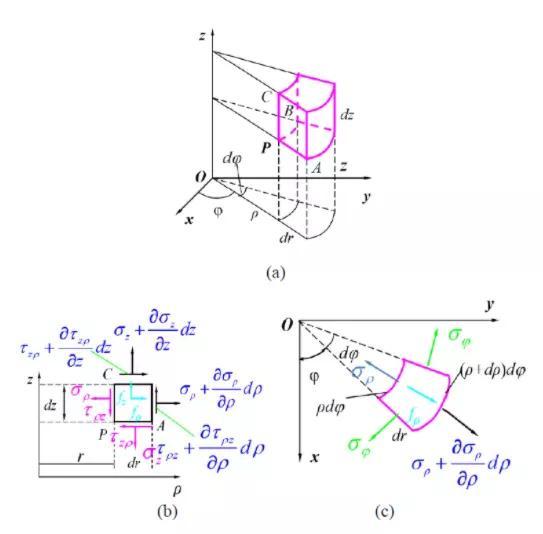
图6 空间轴对称问题微元体模型
列出极径方向（ρ 方向）的平衡方程，有ΣFρ=0
列出轴向（z 方向）的平衡方程，有ΣFz=0
列环向（φ 方向）的平衡方程，有ΣF𝜙≡0为恒等式。因此，空间轴对称问题的平衡方程为
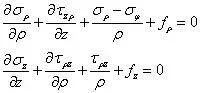
至此，我们已经看到，对于空间轴对称问题，平衡方程有2个，几何方程4个，物理方程4个，共十个基本方程，未知量包括2个位移分量uρ、w，4个应变分量ερ、εφ、εz、γzρ 和4个应力分量σρ、σφ、σz、τzρ，共十个未知量，构成封闭方程组。
想象一下，求解空间轴对称问题基本方程时，由于平衡方程和几何方程为微分方程，必然会存在积分常数，需要借助应力边界条件和位移边界条件来确定。
首先说应力边界条件，由于柱坐标也是正交坐标系，因此仿照直接坐标系，可以写出柱坐标系的边界条件，如
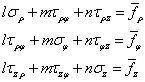
由于τzφ=0和τρφ=0，且轴对称条件下可导出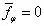
。因此，上式变为
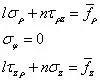
其中，l 为表面外法线与ρ 方向夹角的余弦，m 为表面外法线与φ 方向夹角的余弦，n 为表面外法线与z 方向夹角的余弦。我们以圆柱体（图7(a)）和圆锥体（图7(b)）为例，写轴对称问题的边界条件。
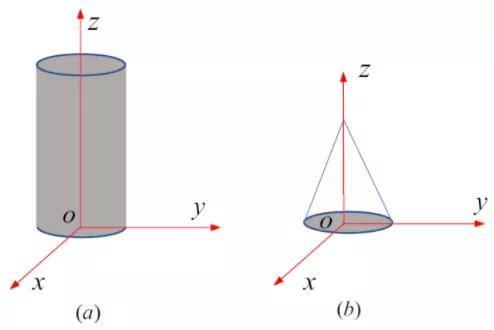
图7 空间轴对称问题边界条件示意图
先考虑圆柱体，它有三个表面，上下圆面和圆柱面。在圆柱面上，ρ=a 时（设圆柱体的半径为a），l=1，n=0，讲其代入边界条件（上式），有
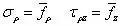
在底面上，z=0时，l=0，n=-1，将其代入边界条件，有
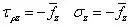
在顶面上，z=h 时（设圆柱体的高度为h），l=0，n=1，将其代入边界条件，有
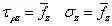
再考虑圆锥体，它有两个表面，圆锥面和底面，设圆锥体的顶角为θ，高为h，将圆锥体想象成许多圆面，每个圆面的半径为(h-z)tanθ。
在圆锥体锥面上，ρ=(h-z)tanθ 时，l=cosθ，n=sinθ，代入边界条件，有
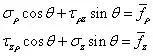
在底面上，z=0时，l=0，n=-1，将其代入边界条件，有
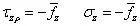
以上即为空间轴对称问题的应力边界条件。考虑位移边界条件时，由于φ 方向的位移恒等于0，即uφ=0，只需要分析约束在oρz 平面内的位移约束分量，即边界处uρ、w，以及əuρ/əz（或者əw/əρ）。对于实际工况，可考虑约束是否限制了边界处的线位移和角位移，例如三个位移都被约束的情况，可写成
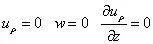
也可能是其中的两项被约束，或者一项被约束，需要根据实际工况进行判定。对于多连体，位移边界条件还需要考虑位移单值条件。
参考资料：徐芝纶. 《弹性力学》（第5版）. 高等教育出版社.
