流体力学之"漂洋过海来看你"

来源：LBM与流体力学，作者：卢比与钢蛋。

机翼两端的翼尖涡深深的吸引住了Batchelor，“我看不懂，但我大受震撼”。当时的澳大利亚还没有设置博士学位，但这并不妨碍Batchelor 对流体知识探索的一片热忱。1940年11月，硕士毕业的Batchelo r毅然选择留在CSIR 继续从事气动研究工作。当时的澳大利亚还处于二战的关键时刻，Batchelor 在CSIR 的主要工作也变成了为飞机排查气动相关的故障。尽管Batchelor 也觉得这份工作没那么有趣，不过他一直尽职尽责，而这些实际的工程问题也让Batchelor 对于流体力学有了更深刻的认识。

"书到用时方恨少"，随着工作的开展，Batchelor 愈发觉得自己对于流体力学缺乏系统的认知，尤其是高雷诺数的流动。于是Batchelor 大量阅读流体相关的书籍和文献，而作为整个流体力学领域最重要也最困难的话题——湍流，也引发了Batchelor 最大的好奇。

随着二战进入后期，Batchelor 开始有了一些空闲的时间，当然也受到了Taylor、Karman 等人在1930年代的工作启发，于是Batchelor 也开始在风洞中复现均匀湍流的发展，并尝试对湍流进行完整的数学描述。当然后来的我们都知道，Batchelor 和他的诸多同行逐渐演绎出湍流理论的统计学派，也就是我们常说的流体气宗。

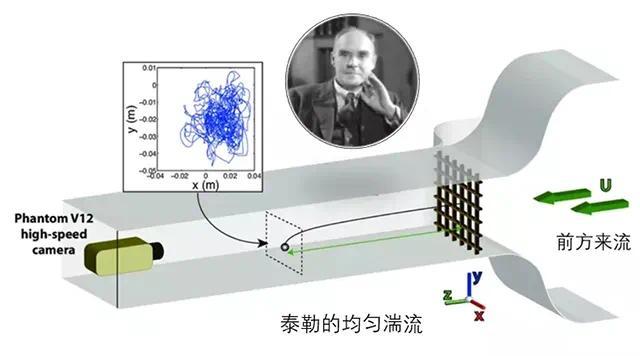
到了1944年，二战即将结束，24岁的Batchelor 也开始考虑他未来的学术之路，他给远在英国剑桥的Taylor 写信，申请攻读湍流方向的博士学位。面对如此青年才俊，Taylor 欣然同意，还建议Batchelor 可以使用卡文迪许实验室的小型低湍流度的风洞来进行相关的研究。Batchelor 虽然大受鼓舞，可是他却不太擅长做实验。

不过行走在流体江湖上，向来靠的都不是单打独斗，比如欧拉和伯努利，柯尔莫果洛夫和亚历山德罗夫，卢比和钢蛋。Batchelor 也有一位“一生一世一起走的好基友”，此人便是熟悉各种测试设备和实验的Alan Townsend，他也是Batchelor 在澳大利亚的同事。Townsend 原本打算去剑桥攻读核物理的博士，却被Batchelor 劝说和他一起拜入Taylor 的门下，攻读湍流的博士。“好基友”的魅力大概就是“你说什么，我都信。” Townsend 几乎没有任何犹豫，就答应了Batchelor。

后来的事实也证明了，这对好友成为了湍流理论研究的黄金搭档，Batchelor 负责理论部分，并站在台前，向学术圈发声，而Townsend 承包了全部的实验，并且在幕后为Batchelor 出谋划策。他们在随后的几十年的时光里，提出了无数精彩的理论。

1945年，二战刚结束，Townsend 和Batchelor 飘洋过海来到了剑桥大学。尽管是战胜国，英国也受到了很大的创伤，那是一个物资匮乏、百废待兴的时代，而两位年轻人还是因为能够进入剑桥大学三一学院而感到单纯的幸福。

作为全球的科研圣地，三一学院有着悠久的历史，也诞生了无数的科学大家，牛顿、麦克斯韦、瑞利、汤姆森、泰勒等等，他们在前面指引着两位年轻的学者。而Townsend 和Batchelor 也幻想着读博期间，他们会聆听各位顶级学者的课程和报告，与大师们一起在知识的海洋里翱翔。

Townsend 和Batchelor 很快便迎来了和Taylor 的第一次正式交流，然而Taylor 却说他现在已经不研究湍流了。从1940年开始，因为二战的原因，Taylor 的主要研究方向转成了空气和水下爆炸中的波传播问题，他也因此参与了著名的曼哈顿计划。两位年轻的学者面对这个突然的情况简直是一脸懵逼，不过所幸，Taylor 在之前已经为他们奠定了湍流理论研究的基础。

于是在整个博士期间，Batchelor 和Townsend 的绝大部分工作都是自己独立思考和设计的。不过Batchelor 后来也在回忆录中说过，尽管Taylor 没有直接参与到他们的湍流研究中，但是每次他们找Taylor 讨论问题的时候，Taylor 总能给他们提供很好的建议，或者为他们指引一些重要的方向。尽管这种科研的方式在一开始的时候给Batchelor 和Townsend 带来了一些挑战，然而却大大激发了两位年轻学者的独立思考能力，他们也迅速的适应这种状态并渐入佳境。

在剑桥的学习生涯中，除了可以直面各位大师，图书馆也成为了Batchelor 汲取知识的琅嬛玉洞。关于湍流理论，Batchelor 在图书馆中发现了第一盏指路明灯，也是对其研究影响最大的人——湍流理论的集大成者柯尔莫果洛夫。早在1941年，柯老仙便在苏联分别用俄语和英语发表了著名的K41理论，其中英文版本在战争期间传播到了剑桥。

在图书馆的众多文献中，Batchelor 第一次看到柯老仙的K41理论：基于前人通过实验给出的湍流能级串理论，柯老仙大胆假设，惯性尺度范围的涡不仅不受大尺度各向异性涡的影响，也不受耗散尺度涡的影响，其含能仅取决于能量传递速率ε，与粘性也无关。随后，柯老仙使出了一招平平无奇的量纲分析，给出了湍流世界最著名的-5/3幂律。

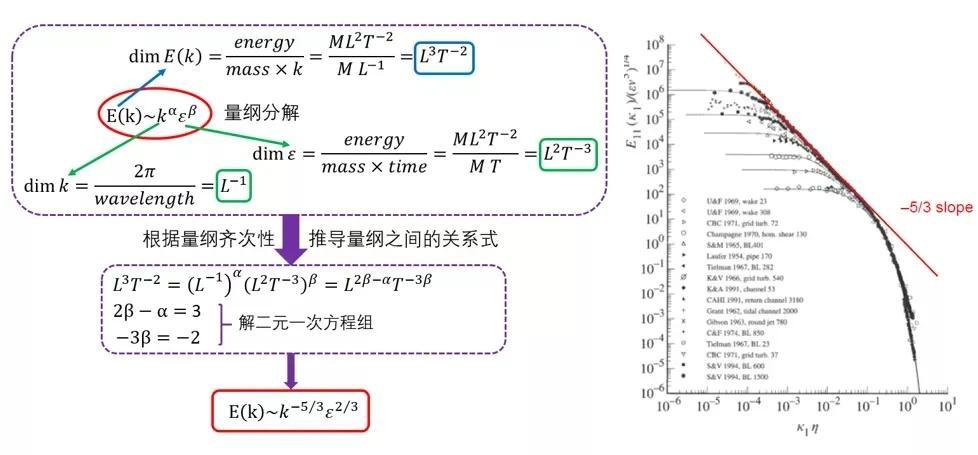
柯老仙的论文仅用了四页纸就奠定了湍流理论的基础，而对于Batchelor 这个初出茅庐的少侠而言，无疑是一件神兵利器，Batchelor 也由此开启了在湍流世界的翱翔之旅。

随后的时间里，Batchelor 发现，除了柯尔莫果洛夫之外，也有其他两位学者在相近的时间做着同样的事情，也得到了类似的结果，一位是获得过诺贝尔奖的美国化学家Lars Onsager，而另外一位则是传奇的德国理论物理学家Von Weizsäcker。

二战结束后，盟军将所有可能参与核武器研制的德国科学家都集中起来，并带到了英国，其中有一部分科学家就住在剑桥附近的一个大房子里面，曾经在读博期间被导师索末菲的湍流触发机理折磨到要去找上帝问问清楚的海森堡和他的学生兼助手Weizsäcker便在其中，两人在空闲的时间，经常躺在草地上，观察云层中的湍流变化，就是在这样的观察和讨论中，Weizsäcker 想到了和柯老仙类似的方法来描述湍流。由于导师Taylor 可以去拜访这些德国科学家， Batchelor 也因此能够从Taylor 那里了解到这些大神的思想。

1945年后，随着战后重建的如火如荼，湍流理论也伴随着K41理论的广泛传播进入到了一个蓬勃发展期，尤其是在剑桥大学。而众多学者通过理论和实验逐步验证了K41理论的-5/3幂律也给了Batchelor 极大的鼓舞。在众神的基础上，Batchelor 进一步扩展了对于均匀湍流的认识，并在1953年写成了经典著作《The theory of homogeneous turbulence》。

而那时的剑桥大学也在Taylor和Batchelor的带领下，俨然成为了湍流理论研究的中心，Batchelor也慢慢接替了Taylor的位置，成为了剑桥湍流研究的掌舵者。

1961年，为了庆祝即将在法国成立的湍流统计研究所，一众湍流理论的大神齐聚马赛，举办了一场颇具传奇色彩的研讨会。作为剑桥湍流研究的新掌门， Batchelor 已成为流体气宗中举足轻重的人物，他也是这次会议的主要组织者。

这场会议成为湍流历史上一次重要的会议，连一向很少外出访问的柯尔莫果洛夫也从苏联来到了法国，他的学生和同事奥布霍夫、雅格洛姆也一起出席了会议。欧美流体力学界的两位领军人物冯·卡门和泰勒也在，当然还有很多其他著名的流体力学家，比如Stan Corrsin、John Lumley、Philip Saffman、Les Kovasznay等学者也都参加了这次盛会。

当时的K41理论仍然深入人心，而Bob Stewart 首先展示了温哥华岛和加拿大大陆之间潮汐通道的海洋湍流能量谱的测试结果，结果完美印证了柯尔莫果洛夫的-5/3幂律。正当众人欢欣鼓舞的时候，柯老仙走上讲台，他指出，就在他发表K41理论之后不久，另一位俄国的理论物理学家朗道便指出了他的理论中存在缺陷。

柯尔莫果洛夫在演讲中解释：湍动能会按照一定的速率从大涡向小涡传递，在流场的不同位置处，传递速率会不同，但是随着雷诺数的增加，不同位置处的瞬时耗散率将具有越来越不均匀和明显的间歇性分布，还有一些和小涡相关的统计量同样会出现大的波动，并且这些统计量之间以不同方式受到波动影响的关系都不具有K41理论预测的普遍性，当然这些都和雷诺数相关。

柯尔莫果洛夫和奥布霍夫进一步介绍，如果假设流场中的当地耗散率具有对数正态分布，则波动的影响仅需要对湍流动能谱函数中的波数功率进行小的修正，但湍流理论的问题仍然存在。当然，究其原因或许还是湍流问题本身的复杂性吧。

尽管柯老仙说着不太流利的法语，但是参会的一众大神们还是清晰的理解了他的意思，在后来一些学者的回忆录中，甚至将柯老仙的那场报告形容成了湍流理论研究的分水岭，在那以后，学者们都觉得想要通过统计理论完整的描述湍流几乎是不可能的。

尽管早在1950年代，Townsend 和Batchelor 就已经通过实验发现了湍流运动中小尺度涡的间歇性问题，但是听到偶像柯尔莫果洛夫的解释，坐在台下的Batchelor 或许也在心中感慨“湍流终究是湍流”。而这次马赛之行也对Batchelor 理想中的湍流大一统理论蒙上了一层阴影。

在马赛会议之前，Batchelor 花了15年的时间研究湍流理论，然而随着对湍流的研究不断深入，Batchelor 也逐渐感觉到想要用确定的理论来描述湍流几乎是不可能的。已经人过中年的Batchelor 感到一些失落，想要切换到其他的研究方向，可是湍流问题仍然萦绕在他的心头。后湍流理论的时代，Batchelor 何去何从？他又如何在新的时代创造新的经典和顶流？敬请期待下回分解。