CATIA软件中画抛物线的四种方法讲解
来源:CATIA小蚂蚁
抛物线的概念
抛物线Parabola是指在笛卡尔平面内,到定点(焦点)与定直线的距离相等的点的轨迹。其中定点F叫抛物线的焦点,定直线L叫抛物线的准线。抛物线的最通俗的定义,就是:即把物体抛掷出去,落在远处地面,这物体在空中经过的曲线。这个通俗的解释所蕴含的原理,支撑了抛物线在光学、力学和工程学上的应用。
另外我们需要学习一下抛物线的焦点求解,焦点就是我们前面所说的定点哦,初中知识复习如下:
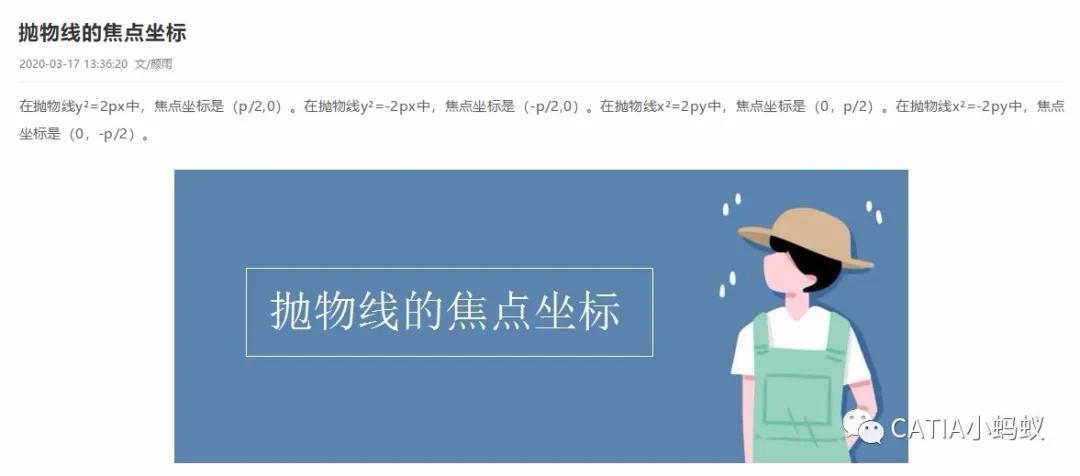
对于抛物线x²=4py,焦点即为(0,p),那么y=x²的焦点坐标是(0,1/4),这里的P=0.25,今天就来说一说在CATIA软件中绘制抛物线Y=X²的四种方法!
第一种方法,在草图模块,通过焦点创建抛物线 命令
我们首先要创建好四个点,即焦点,顶点,起始点和结束点,点击命令之后依次选择即可,如下即为通过此种方法绘制草图的界面
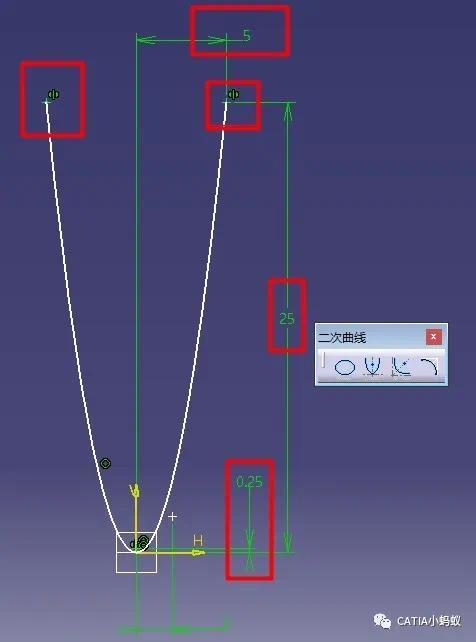
第二种方法,在GSD模块,二次曲线命令
但是我们依然需要进行前期操作,我们依然选好起始点和结束点,并绘制y=x²在此两个点的切线,对此函数求导函数公式为y=2x,那么在(5,25),(-5,25)两个点的导数(即斜率)分别为10和-10,我们在这个位置画出这两条直线,然后通过二次曲线命令求出曲线即可,如下图操作
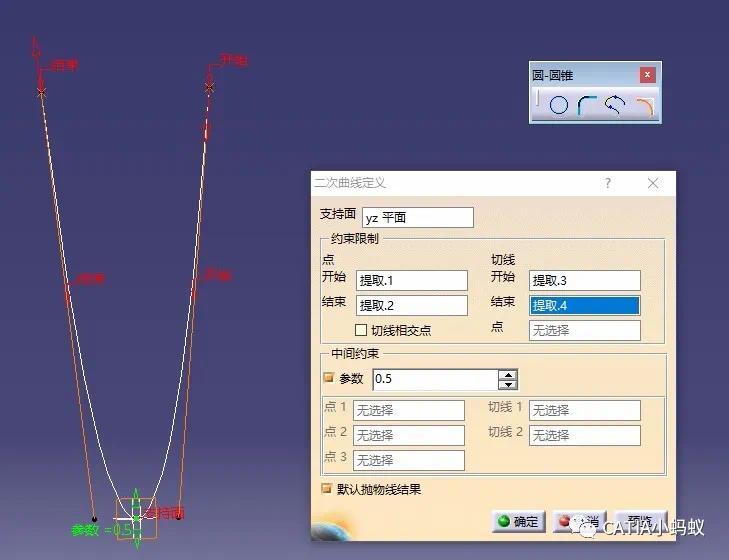
第三种方法,平行命令按照法则曲线fog偏移,
先在x轴上绘制一条直线,然后采用GSD曲面中的parallel 命令按照法则曲线进行偏移,如下流程
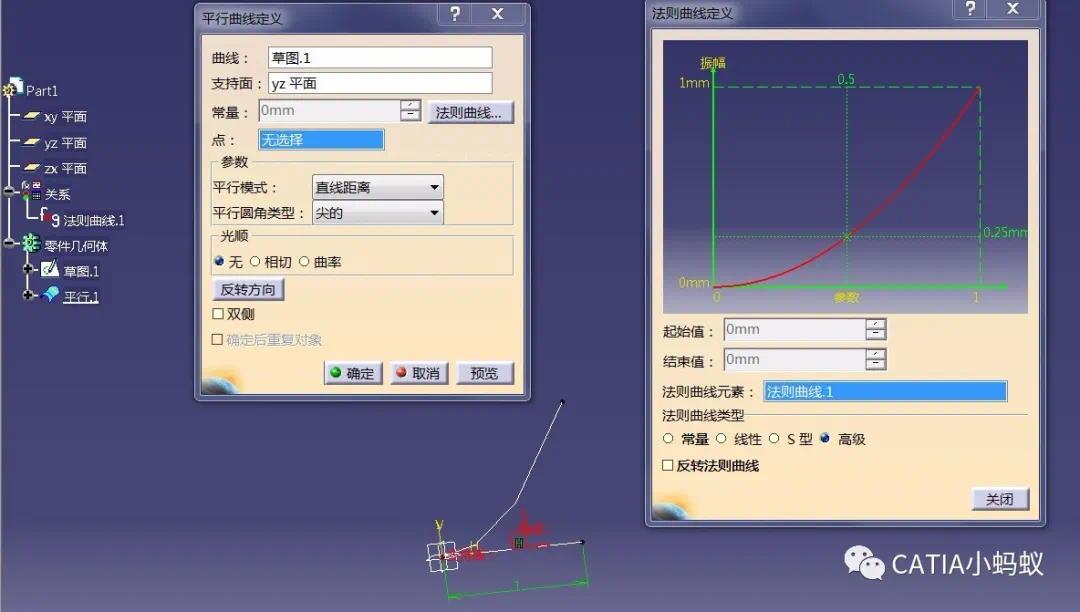
1,先定义法则y=x²

2,点击平行曲线命令,并按照法则曲线偏移
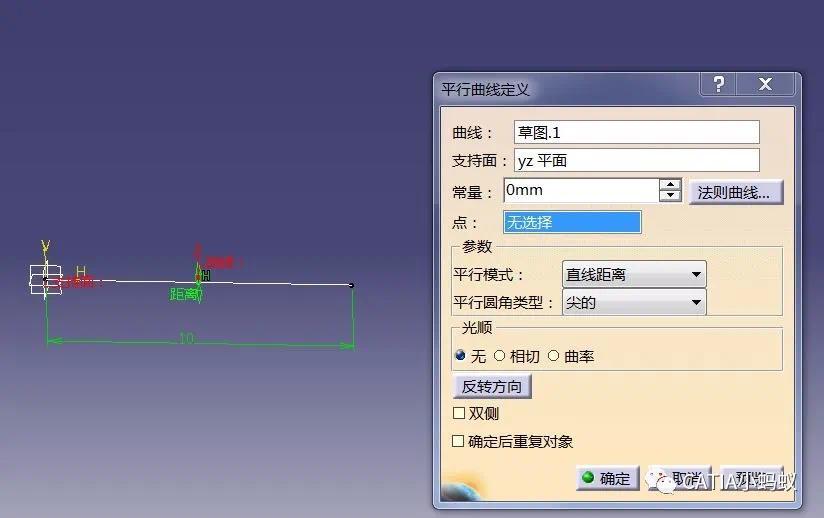
3,如下得到y=x²的抛物线的第一象限函数曲线,再做对称即可
第四种方法,自然就是我们一直以来要学习的二次开发,
我们在y=x²上按照距离单位进行取点,然后采用样条曲线依次连接,自然,取点越多间距越小,绘制出的样条曲线越接近我们要求的抛物线曲线
编程代码如下,
Sub CATMain() Set partDocument1 = CATIA.ActiveDocument Set part1 = partDocument1.Part Set hybridShapeFactory1 =part1.HybridShapeFactory Set hybridShapeSpline1 =hybridShapeFactory1.AddNewSpline() hybridShapeSpline1.SetSplineType 0 hybridShapeSpline1.SetClosing 0 For i = -10 To 10 Step 0.1 Set hybridShapePointCoord1 =hybridShapeFactory1.AddNewPointCoord(i, i * i, 0#) Set hybridBodies1 = part1.HybridBodies Set hybridBody1 = hybridBodies1.Item("几何图形集.1") hybridBody1.AppendHybridShapehybridShapePointCoord1 Set reference1 =part1.CreateReferenceFromObject(hybridShapePointCoord1) hybridShapeSpline1.AddPointWithConstraintExplicitreference1, Nothing, -1#, 1, Nothing, 0# Next hybridBody1.AppendHybridShapehybridShapeSpline1 part1.Update End Sub |
动画演示如下

the end





