艾力应力函数法
来源:力学酒吧,作者:张伟伟。
本文将介绍力法求解二维问题的一种杰出方法,该方法将应力分量(矢量)用一个势函数(标量)表示,这样就相当于进行了进一步消元,把3个未知的应力分量(矢量函数)用1个未知的势函数(标量函数)来表示,大大简化了弹性力学方程组的求解。
19世纪大量铸铁材料应用于桥梁工程,为了确定桥梁结构的强度,亟需有一种求解桥梁内部的应力、应变的方法。这一情况受到了英国数学家和天文学家的艾力 (George Biddell Airy, 1801-1892) 的关注,他意识到求解梁内部所有点应力、应变的重要性,并决定发展一套全新的弹性理论。
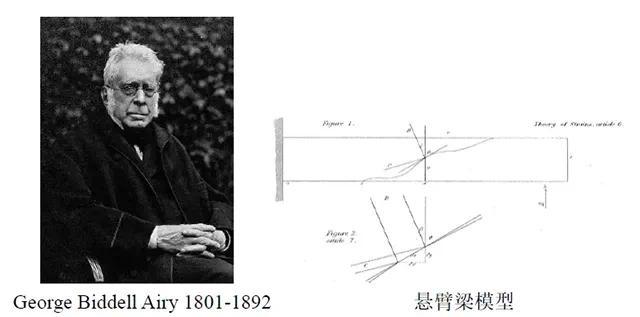
图1 艾力与他分析的悬臂梁
艾力以图1所示的悬臂梁为研究对象,右端下方有向上的集中力R 作用。艾力将悬臂梁视为平面应力问题,画出任意一条曲线,其上选一微元体,写出微元体的平衡方程,并导出了一个势函数用于表示微元体上的力,这个势函数就是现在的艾力应力势函数,这一求解二维弹性力学问题的方法被称为艾力应力函数法。
在艾力的时代,微元体的选取、以及应力的表达还没有固定的形式,这给我们理解艾力的原文带来的一定的困难。随着弹性力学理论的不断完善,后来的学者简化并完善了艾力应力函数法。这里,我们以平面应力问题为例,介绍艾力应力函数法的求解过程。
力法求解二维问题的基本方程,包含2个平衡方程和1个变形协调方程(相容方程)
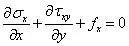
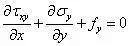

当体力为常数时,上式右侧为0,即可得到常体力下的相容方程

再来看式
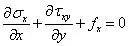
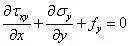
从微分方程的形式看,它们为非齐次微分方程。在微分方程中学过,非齐次微分方程的解可以分解为对应齐次方程的通解,加任意一组特解。我们先考虑其对应齐次方程
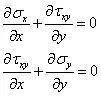
对齐次方程做如下变换
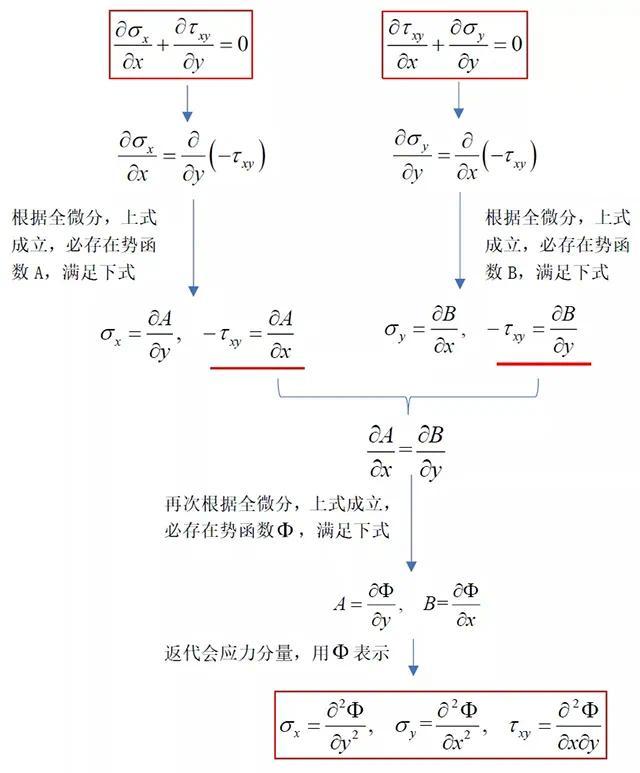
在下式中,式函数Φ,即艾力应力函数。
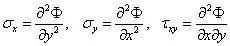
已经看到,三个应力函数由一个势函数Φ 表示,相当于3个未知量消元为1个。上述求解过程中所用到的微积分定理也很容易验证,例如,函数A 可以写成全微分形式
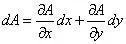
令

当σx 和τxy 在单连通区域内具有一阶导数时,从而
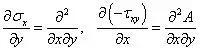
因此,有
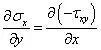
逆过程就是下面推导式时用到的微积分定理。
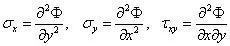
当应力分量用应力函数表示后,只要求得应力函数Φ,就可以获得齐次方程的通解。现在来考虑特解,观察下式至少可以写出三组特解:
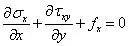
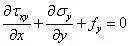
特解一:
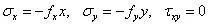
特解二:
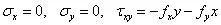
特解三:

不妨选择特解一(其它类似),写出弹性力学二维问题的全部解为
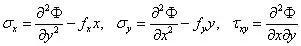
将上述应力分量代入常体力下的相容方程
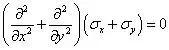
有

即
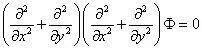
或者
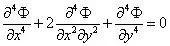
微分算子 (ə²/əx² ə²/əy²) 写成▽²,称为拉普拉斯算子。因此上式也写为
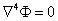
满足下式的函数被称为重调和函数。
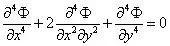
在求解弹性力学问题时,如果体力为常数,先利用上式确定出应力函数Φ,再利用下式写出通解,
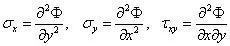
如果需要考虑体力,在通解上叠加任意一组特解,就得到弹性力学的全部解。
由于下式为微分方程,求出的Φ 一般含有积分常数,这就需要用到边界条件来确定。对于多连体,有时还需要考虑位移单值条件。
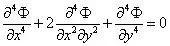
可见,艾力应力函数法求解弹性力学问题的关键在于求出满足上式的应力势函数。但是,应力势函数通常情况下不能直接求解,一般有两类方法确定应力势函数,分别为逆解法和半逆解法。
逆解法,也可以称之为经验法,即先设出某种类型的满足相容方程的函数,然后求解应力分量,再依据应力分量求出面力分布,这样就可以知道哪类弹性力学问题应该选择什么样的应力函数。
半逆解法,就是针对特定的问题,根据边界条件,确定出全部或部分应力分量为某种形式,也可以通过量纲分析,确定出应力函数与坐标或弹性体几何特征之间的某种关系,从而推出应力函数,然后检验其是否满足相容方程,以及原来所假设的应力分量和由这个应力函数求出的其余分量,是否满足边界条件。如果相容方程和边界条件都满足,就得到了正确的解;否则需要重新设定,重新检验。
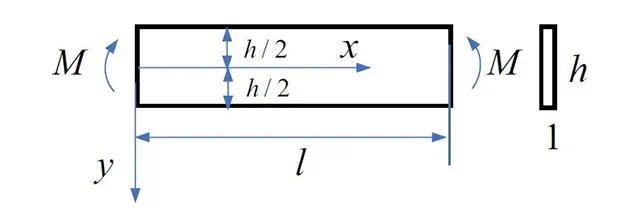
图2 求两端受力偶作用梁的应力分布
解:
第一步,先检验应力函数Φ=ay³ 是否满足相容方程,将其代入相容方程,经检验满足相容方程。
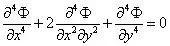
第二步,写出应力分量。
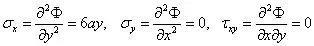
第三步,将应力分量代入边界条件。
上边界,y=-h/2时,σy=0,τxy=0(自然满足)
下边界,y=h/2时,σy=0,τxy=0(自然满足)
左边界,x=0时,利用圣维南原理写等效边界条件
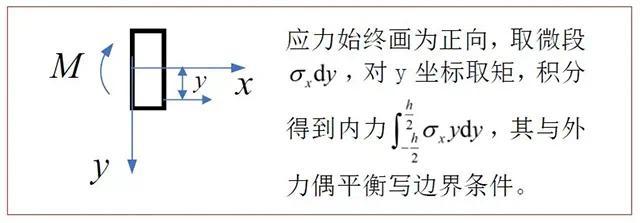
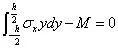
将σx=6ay 代入边界条件,得
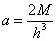
第四步,代入应力表达式,得
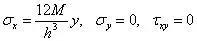
分析:对于矩形截面梁,惯性矩满足
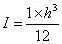
因此,应力分量又可以写为
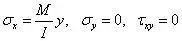
这一结果与材料力学纯弯曲梁的应力解完全一致。在获得应力解后,代入物理方程(广义胡克定律)可得到应变分量,再通过几何方程,可得到位移分量,由于几何方程为微分方程,求位移分量时会出现新的积分常数,这需要再借助于位移边界条件。上述例子中,没有考虑体力,如果需要考虑体力,只需要在第二步写出的应力分量中,叠加任意一组特解,然后使得全部解满足边界条件即可。
参考文献
徐芝纶. 《弹性力学》(第五版). 高等教育出版社
George Biddell Airy. On the Strains in the Interiorof Beams. Philosophical Transactions of the Royal Society of London , 1863,Vol. 153 (1863), pp. 49-79.





