做好弹塑性分析的六大基础!
与弹性分析不同的是,在弹塑性分析中,我们还要知道材料受力到什么程度才开始发生塑性变形。在简单拉伸时,答案是很明显的,即引起塑性变形是因为应力达到了材料的屈服极限,而屈服极限是可以在拉伸曲线上找到的。然而在复杂应力状态时,问题就不这样简单了。
某一点的应力状态是由六个应力分量确定的,显然我们不应该任意选取某一个应力分量的数值作为判断材料是否进入塑性状态的标准。为此,我们要引进应力空间和应变空间的概念,它们分别是以应力分量和应变分量为坐标的空间。在这些空间中,每一点都代表一个应力状态或一个应变状态,应力或应变的变化在相应的空间中绘出一条曲线,称为应力路径或应变路径。
根据不同的应力路径所进行的实验,可以定出从弹性阶段进入塑性阶段的各个界限。在应力空间中将这些屈服应力点连接起来,就形成一个区分弹性与塑性的分界面,称为屈服面。描述这个屈服面的数学表达式,称为屈服函数或称为屈服条件。
屈雷斯加 (H.Tresca) 根据自己的实验结果,认为最大剪应力达到某一数值时材料就发生屈服。即

即最大剪应力条件或屈雷斯加条件。它表示主应力空间内与坐标轴成等倾斜的各边相等的正六角柱体(如图1所示),通常称为屈雷斯加六角柱体。
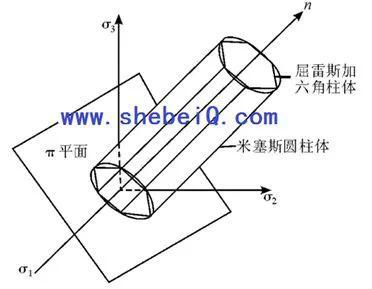
图1 Tresca六角柱体和Von Mises圆柱
畸变能条件认为,与物体中一点的应力状态对应的畸变能达到某一数值时该点便屈服。以主应力表示的畸变能屈服条件为
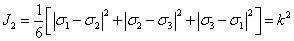
其中,k 为表征材料屈服特征的参数,可由简单拉伸屈服实验确定。此畸变能条件系米赛斯 (Von Mises) 所提出,故称为米赛斯条件。可以看出米赛斯条件在主应力空间是对坐标轴σ1、σ2、σ3 为等倾斜的圆柱体,通常称之为米赛斯圆柱。进一步分析可以证明,米赛斯圆柱外接于屈雷斯加六角柱体。
以上两种屈服条件各有优缺点,最大剪应力条件是主应力分量的线性函数,因而对于已知应力方向及主应力间相对值的一类问题,是比较简便的;而畸变能条件则显然复杂得多。但从理论上讲,最大剪应力条件忽略了中间主应力对屈服的影响,而畸变能条件则克服了这一不足。实验证明:畸变能条件比最大剪应力条件更接近于实验结果。
掌握以上六点,是用好弹塑性分析的必要基础。





