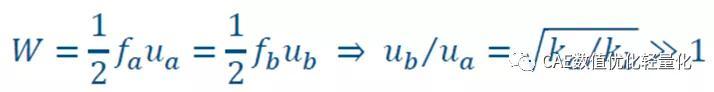ABAQUS屈曲分析之一(线性特征值屈曲分析)
结构稳定性问题是我们日常生活中经常遇到的问题,主要是发生在梁或壳结构中。

屈曲是一种失效模式,其特征是构件在高压应力作用下突然失效。屈曲失效的实际压应力小于材料能够承受的最终压应力。当构件或结构将膜应变能转换为弯曲应变能而外部施加的载荷不变时,会发生屈曲失效。

一个长为L的细长杆,横截面积为A。轴向刚度ka远大于弯曲刚度kb。因此,微小的膜变形可以吸收大量的应变能。然而,需要较大的横向挠度和横截面旋转来吸收弯曲中的能量。如果让弯曲来吸收膜应变能,挠度将会远大于轴向变形。
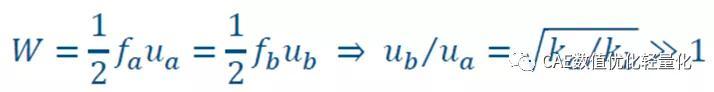
几种典型稳定性问题:
板件屈曲-分支问题:
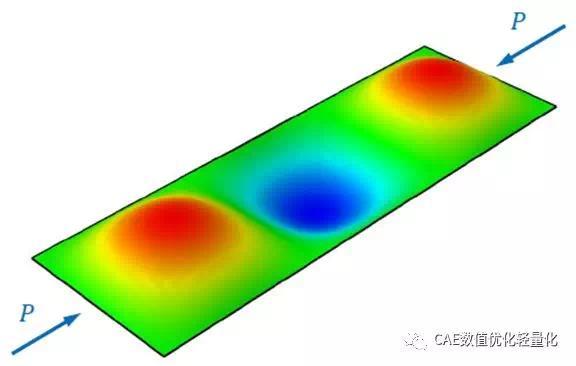
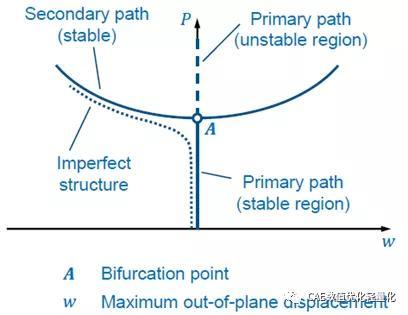
一般情况下,小的初始缺陷对平板的后屈曲响应没有显著影响,但可能影响屈曲方向。突弹跳变(snap-through)-极限载荷问题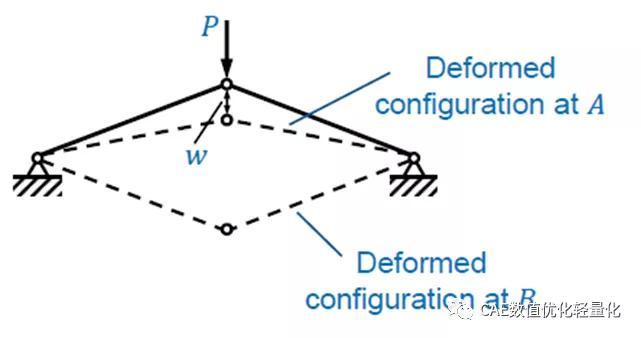
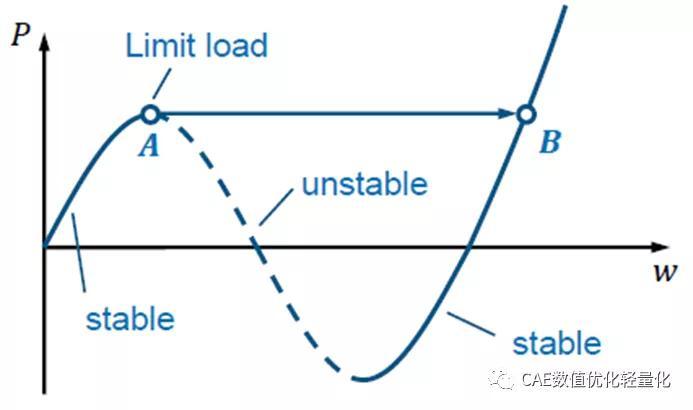
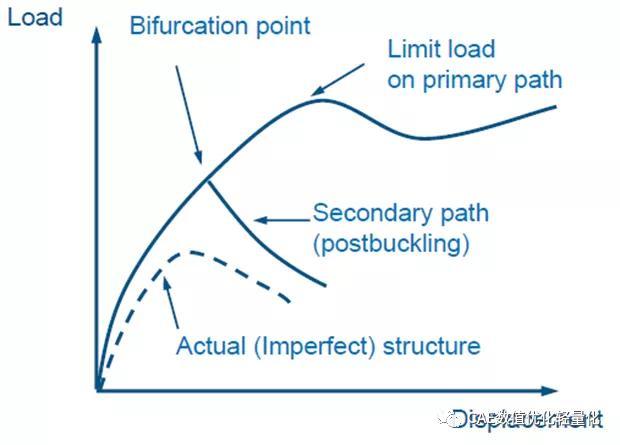
预屈曲段的结构响应是非线性的。因此,需要进行几何非线性分析来准确研究预屈曲行为。结构不稳定发生在一个负载最大(极限载荷𝐴点)位置。一旦解在点A处变得奇异,结构就从A点翻转到B点。在快速翻转过程中,响应变为动态的,结构释放弹性能转化为动能。在B点存在一个稳定的静力平衡状态。超过这一点,载荷P可以再次增加。无加强筋的圆筒屈曲
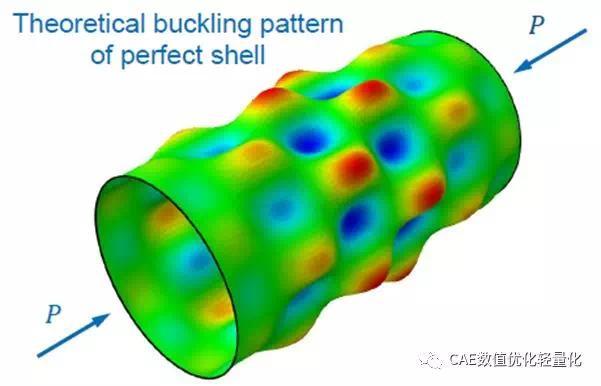
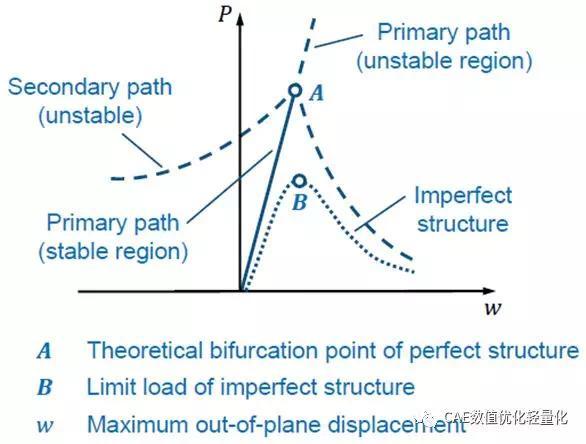
结构对小的初始缺陷表现出很强的敏感性。对初始缺陷的考虑将分岔问题转化为极限载荷问题。
屈曲问题本质特征:
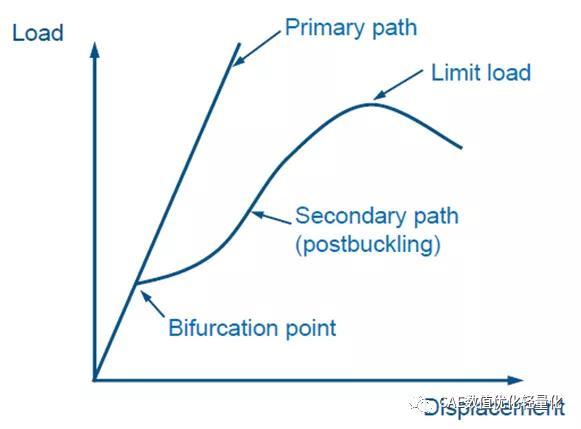
A类问题:在分叉点前为线性响应
缺陷敏感:实际结构的坍塌载荷受载荷方向、支承方式或几何形状的微小变化的强烈影响。这些结构往往是求极限载荷问题。
ABAQUS一般有两种分析手段来处理这类分析问题:特征值屈曲分析和后屈曲分析。 通常用来估计刚性结构的临界屈曲载荷。想要特征值屈曲分析可以得到可靠的屈曲载荷的估计,需要满足以下假设前提:小几何变化、线性弹性材料响应,且缺陷不敏感。如果对于特征值分析出的结构响应、屈曲载荷的估计存在疑问,则可以通过在结构中引入缺陷(屈曲模式的比例形状),并使用通用(非线性)求解来获得完整的前屈曲和后屈曲历史。B:后屈曲和不稳定坍塌失效的几何非线性分析(针对B类问题): 针对于后屈曲和不稳定坍塌失效的几何非线性分析,abaqus可以通过以下几种方法进行求解:实例:经典的框架屈曲问题
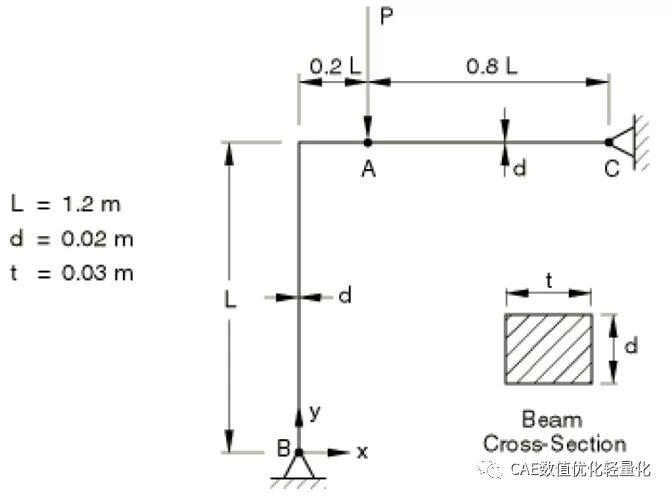
材料属性:E=71.74GPa
约束B、C点的1、2自由度,在A点处承受集中力载荷
ABAQUS中使用B22单元进行分析
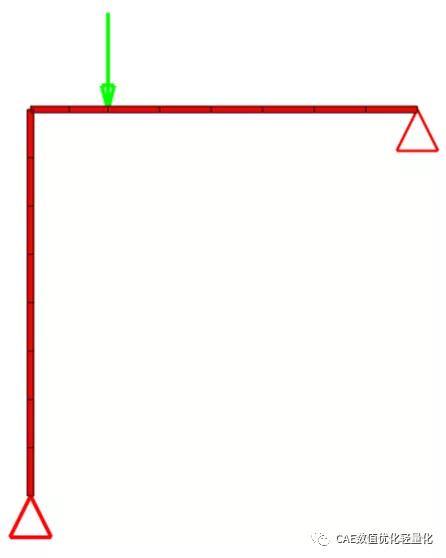
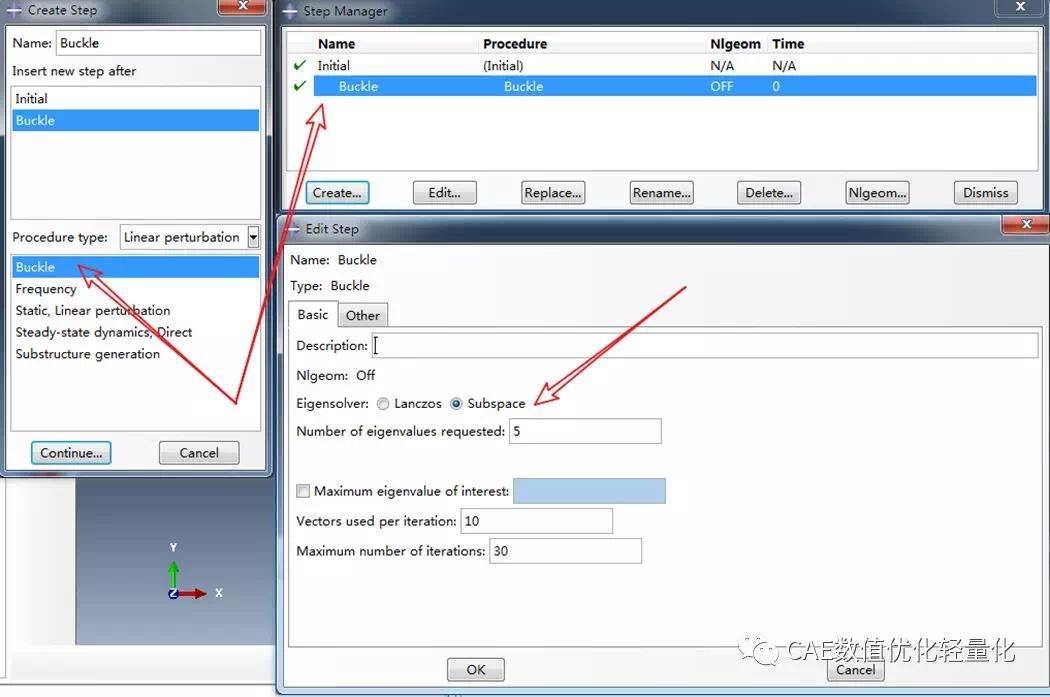
创建Buckle分析步,设置模态提取方法为子空间法,提取5阶模态

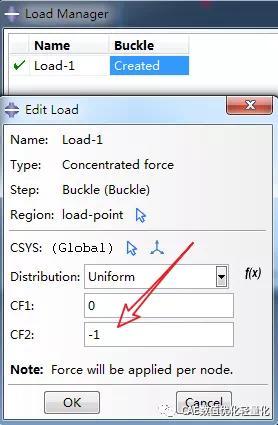
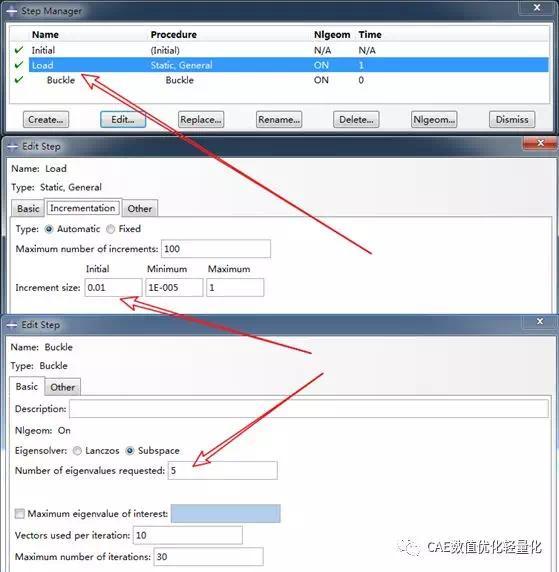
分别创建两个载荷步,首先创建一个非线性分析步,用于施加预载,然后再创建Buckle分析步。打开非线性选项。

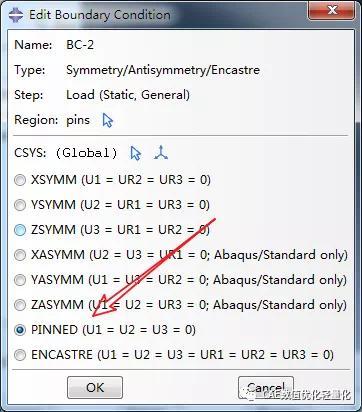
在第一个载荷步中,在A点施加预载10000N,约束B、C点。在第二个载荷步中,载荷及边界条件设置与无预载屈曲分析一致。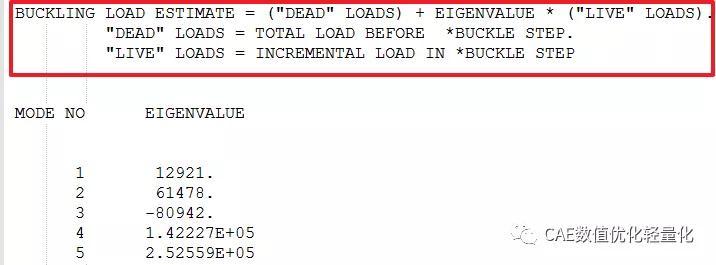
第一阶屈曲载荷为:10000 1*12921=22921N
从结果来看,有预载和无预载的屈曲载荷差别十分巨大,这表明该结构对于初始变形是十分敏感的。因此,需要通过进行非线性分析进行后屈曲分析,获得结构的载荷-位移历程,来详细分析结果的屈曲极限载荷。 我们依次使用几种不同的非线性分析方法来进行对比分析。本文经授权转自CAE数值优化轻量化。

硕士
|
CAE仿真负责人
个人著作《汽车NVH一本通》
获赞 1195粉丝 6725文章 1053课程 21