阻尼比测试方法及谐响应分析!
谐响应分析中,阻尼比的确定是关键问题,工程中阻尼比经常是估计值,导致分析结果跟实际不符。阻尼对模态频率的影响很小,阻尼的主要作用是压低共振处的幅值,如果阻尼取为0的话,共振处的峰值会相当大,理论上是无穷大。目前阻尼问题研究的不是很透彻,并没有很多的理论支持,本文通过试验测试的方法得到板结构的阻尼比,并进行谐响应分析,最后通过振动试验验证了该阻尼测试方法的准确性。
1. 测试原理
自由振动衰减信号的包络线法是一种常用的测量结构阻尼特性的方法。以单自由度为例,说明自由振动的衰减信号的包络线辨识结构阻尼比的原理。有阻尼单自由度系统衰减响应可表达为:
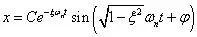
式中,C 为振幅,ωn 为固有频率,φ 为相位角,ξ 为系统阻尼比。可知,单自由度振动的位移衰减信号的包络线方程为:
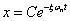
有阻尼单自由度系统衰减响应为位移响应,由于传感器的类型不同,可能获得速度或加速度的时域衰减响应信号。速度及加速度响应表达式:
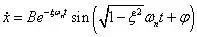
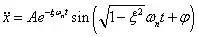
上式与有阻尼单自由度系统衰减响应公式具有相同的数学模型结构,单自由度振动的加速度响应曲线也具有同位移响应曲线相同的包络线,其衰减响应曲线见下图。

图1 自由振动系统响应曲线
由图1,阻尼使系统振动的振幅按几何级数衰减,相邻两个振幅之比:
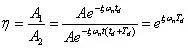
式中,η 为减幅系数,Td 为系统的振动周期,且:
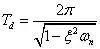
由相邻两个振幅之比得知一个周期内,振幅缩减至初值的1/eωntd。为了避免取指数值的不方便,常用对数减幅δ 来代替减幅系数η,即:

由
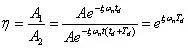
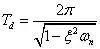
可以得到阻尼比和固有频率的表达式:

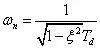
对有阻尼单自由度系统衰减响应取对数:

从上式可看出,lnx 是时间t 的一次函数,如下图所示。
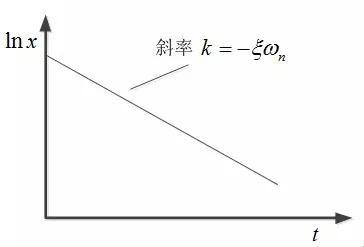
图2 衰减法原理示意图
根据
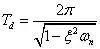
因此,板结构阻尼比很小,存在下式关系:
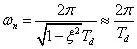
因此,根据图2可得下式:
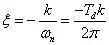
2. 测试分析
对板结构进行阻尼比测试。

图3 悬臂梁阻尼测试
对信号进行巴特沃斯滤波,滤波后的曲线如下图所示。
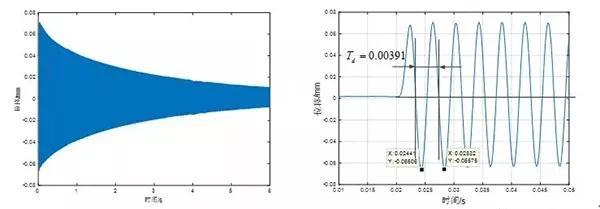
图4 自由衰减位移响应滤波后曲线
对图3的曲线取对数,得下图5的曲线。
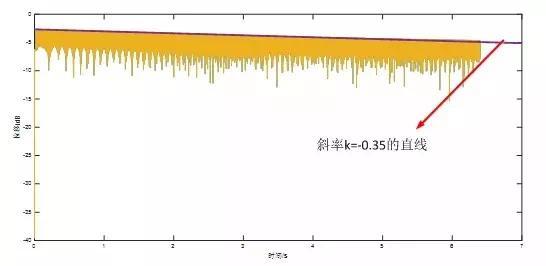
图5 衰减曲线
直线斜率为0.35,Td =0.00391s,根据
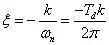
得到板结构阻尼比2.1780e-04。
对上文中的板结构用振动台进行振动试验,与下文中的谐响应分析进行对比。

图6 板结构振动试验
该试验的控制传感器、响应点传感器位置,振动试验方向如下图所示。

图7 控制传感器和响应点传感器
进行正弦扫频振动试验,试验输入条件如下图所示。
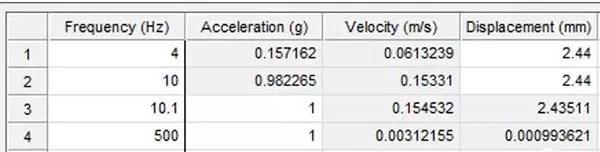
图8 试验输入条件
响应点的响应曲线,如下图所示,可以得到板结构第一阶频率为160.66Hz,最大响应26.97g。
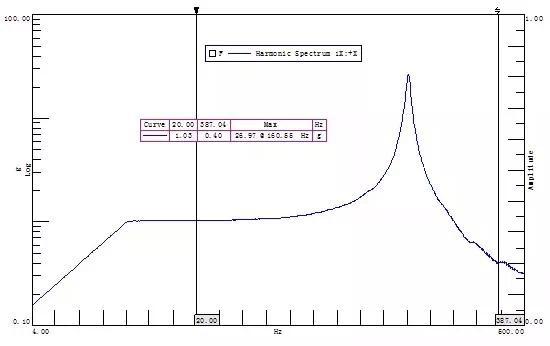
图9 响应点的响应曲线
首先对该板结构进行模态分析,模态的一阶频率为256.2Hz,如下图所示。

图10 模态的一阶频率
板的质量为23.67g,由于在该分析中,传感器和线缆的附加质量不可忽略,板、传感器和线缆总质量为33.67g,因此分析结果的模态频率会比试验结果要低。在传感器的位置添加集中质量重新分析,第一阶模态频率为163.7Hz,与试验误差较小,相符合。

图11 模态的一阶频率
板的质量为23.67g,由于在该分析中,传感器和线缆的附加质量不可忽略,板、传感器和线缆总质量为33.67g。有无附加质量,系统的阻尼是定值,根据上文算出的无附加质量的阻尼比为2.1780e-04,推算有附加质量的阻尼比。已知阻尼的计算公式如下式:
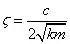
得到
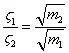
计算出带传感器附加质量的阻尼比为4.407E-4 。将该阻尼比应用到板结构的谐响应分析,得到传感器位置处的仿真的频响曲线与上文的试验曲线进行对比,如下图所示。
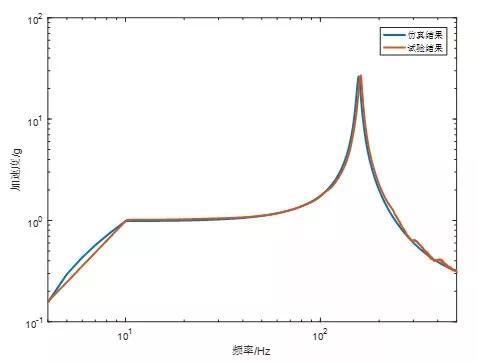
图12 仿真与试验频响曲线对比
从上图的对比结果可知,仿真和试验误差很小,证明本文方法的准确性。





