基于结构应力/应变法的焊接结构抗疲劳设计方法与应用
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐/内容稀缺/全网独家

本文摘要(由AI生成):
本文主要介绍了焊接结构的疲劳特性和疲劳设计方法。焊接结构具有裂纹萌生周期短、疲劳寿命主要消耗在裂纹扩展阶段、焊接结构疲劳具有尺寸效应等特点,动载荷应力幅值为焊接结构疲劳失效的第一驱动力。基于有限元分析的无网格敏感性斜面结构应力法可以有效地描述焊接接头位置的动载荷应力,结合国际疲劳设计标准中S-N曲线族与裂纹扩展速率关系,可以提出一条能够统一描述不同几何形式、不同板厚接头疲劳行为的Master S-N曲线。该方法在2003年SAE“Fatigue Challenge”焊接结构疲劳预测挑战中获得最准确的结果,并以已纳入ASME FFS-1标准等国际标准。
一、写在文前
二、论文作者
王苹 哈尔滨工业大学(威海)海洋工程学院 威海 264209
裴宪军 东南大学机械工程学院 南京 211189;
李向伟 中车齐齐哈尔车辆有限公司 齐齐哈尔 161002
Pingsha Dong University of Michigan Ann Arbor 48109, USA
三、论文摘要
与传统金属材料/小尺寸疲劳试样不同,焊接结构具有其独特的疲劳特性:裂纹萌生周期短、疲劳寿命主要消耗在裂纹扩展阶段、焊接结构疲劳具有尺寸效应,这些因素导致了动载荷应力幅值为焊接结构疲劳失效的第一驱动力。
基于有限元分析的无网格敏感性斜面结构应力法,可以有效的描述焊接接头位置的动载荷应力。该方法结合国际疲劳设计标准中S-N曲线族与裂纹扩展速率关系,可以提出一条能够统一描述不同几何形式、不同板厚接头疲劳行为的Master S-N曲线。该方法在2003年SAE“Fatigue Challenge”焊接结构疲劳预测挑战中获得最准确的结果,并以已纳入ASME FFS-1标准等国际标准。
结构应变方法则是在结构应力方法基础上提出,可以进一步统一描述不同材料焊接构件的高/低周疲劳性能的疲劳评估方法。该方法采用Master E-N曲线将高周疲劳与低周疲劳分析方法统一。目前此方法已经应用于轨道交通、正交异性桥、重型装备等大型复杂焊接结构的疲劳设计与服役寿命预测中,可量化分析焊接变形、焊缝尺寸、熔透率等因素的影响,实现针对复杂焊接结构/接头的抗疲劳设计。
三、论文正文
0 前言*[1]
1 焊接结构的疲劳特性
1.1 材料疲劳 VS 结构疲劳
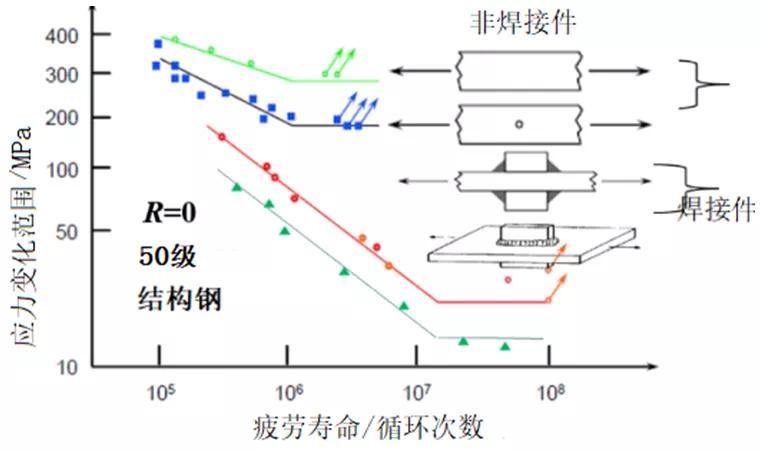
从图中的疲劳试验数据可以看出,同一种均质材料,当结构的局部几何或者宏观几何形式发生变化时,其S-N曲线的位置与斜率发生很大的变化,而焊接试样的疲劳曲线斜率稳定。本文即针对这一问题开展研究,这里要明确的是材料疲劳研究也非常重要,国产新材料试制必须满足疲劳性能要求,在焊接接头各区非均匀性能中要考虑材料变化引起的性能差异,例如铝合金接头中的软化问题。
1.2 焊接结构的疲劳特性
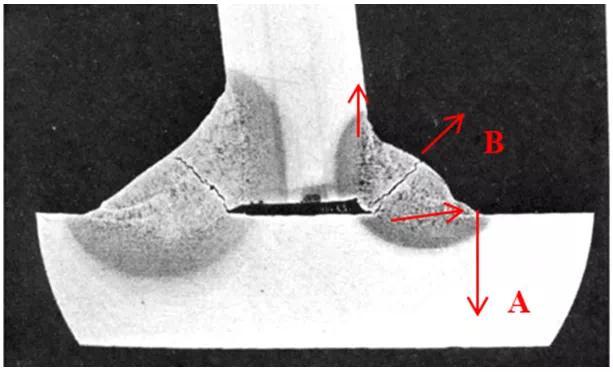
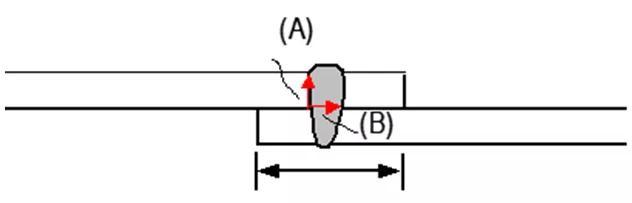
图2 典型焊接接头失效模式示意图
(1)满足一定尺寸要求的焊接构件(标准或者非标准件)其S-N曲线为相互平行的,也就是说具有共同的斜率,斜率接近1/3,而单纯采用均质母材进行试验的斜率不固定,可参见图1;
(2)TWI的疲劳试验数据显示:同种接头类型的焊接结构,即便由不同屈服强度的材料制成,材料的屈服强度范围0~730 MPa,其疲劳数据分布在一个数据带中,这说明结构应力,也就是广义应力集中对疲劳性能的影响远大于材质不均匀引起的差异,参见图3。目前IIW已经将材料强度提升到950 MPa,认为仍满足此项特性[12]。
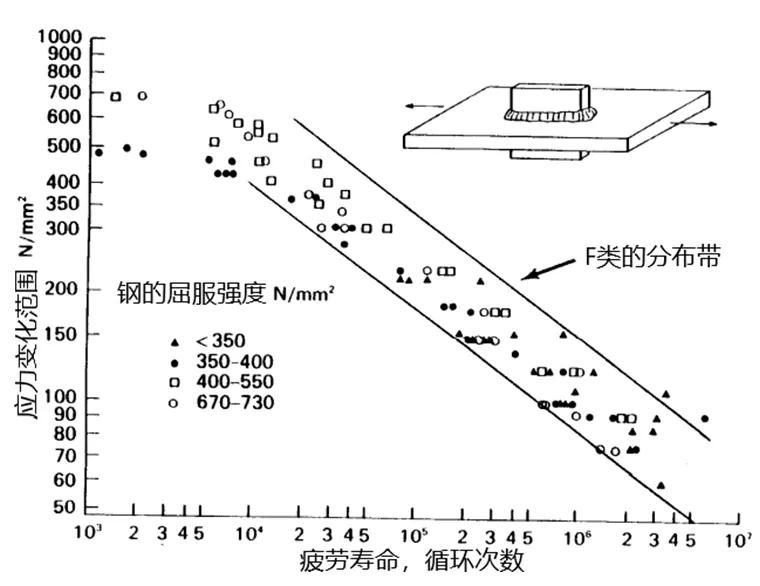
图3 不同材质的Class F接头疲劳数据分布[6]
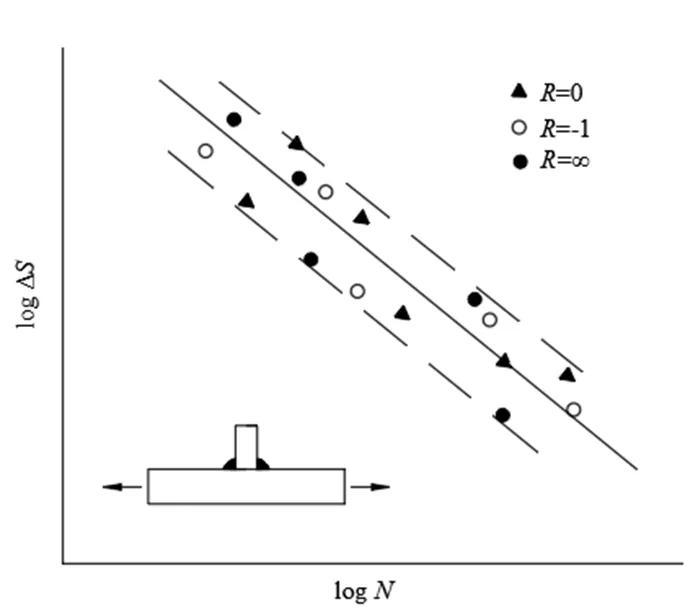
(3)在足尺寸试样疲劳加载中,应力比的影响,即平均应力的影响不用单独考虑,参见图4。当试样的尺寸足够大,残余应力场达到稳定状态时,即满足这一条件,因为残余应力是内应力,为自平衡应力,其影响体现在疲劳试验数据中,因而图4中不同应力比的试验数据仍然分布在一个数据带中。延伸此观点,材料疲劳中的Goodman图不适用焊接结构疲劳设计[13]。
此处提出焊接结构抗疲劳设计的初步建议:
1)焊接结构的疲劳特性与非焊接件大为不同,其疲劳性能与材料自身强度无关,轻量化设计中即使采用高强材料,其结构疲劳性能也不会直接提高;
2)足尺寸焊接构件,其接头存在接近屈服强度的拉伸残余应力,对其疲劳寿命的影响体现在S-N曲线,设计中无需特别考虑,但是不能将材料疲劳数据直接用于设计中;
3)现有国际标准对不同接头类型S-N曲线进行分类处理,说明广义应力集中是控制焊接结构疲劳性能的关键因素,如何量化描述其影响,并降低应力集中系数为设计的重中之重。
2 结构应力法
按照国际疲劳设计标准,描述承载位置的承载参量有:应力/应变或者应力强度因子,从方法上讲有4个不同的层次,即名义应力法、热点/结构应力法、缺口应力法和断裂力学法[14]。各种应力分析方法进一步分为广义和局部。
名义应力为平均应力,属于广义定义,IIW的接头疲劳设计标准给出81个不同结构形式的结构钢和铝合金焊接接头的名义应力S-N曲线,正应力加载时斜率m=3,剪应力加载时斜率m=5[12]。
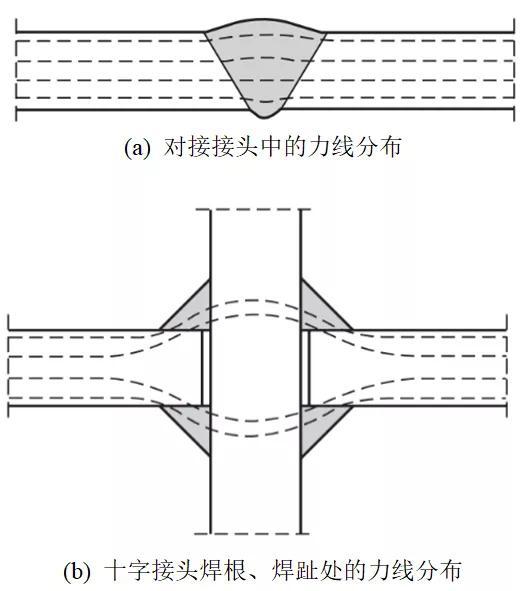
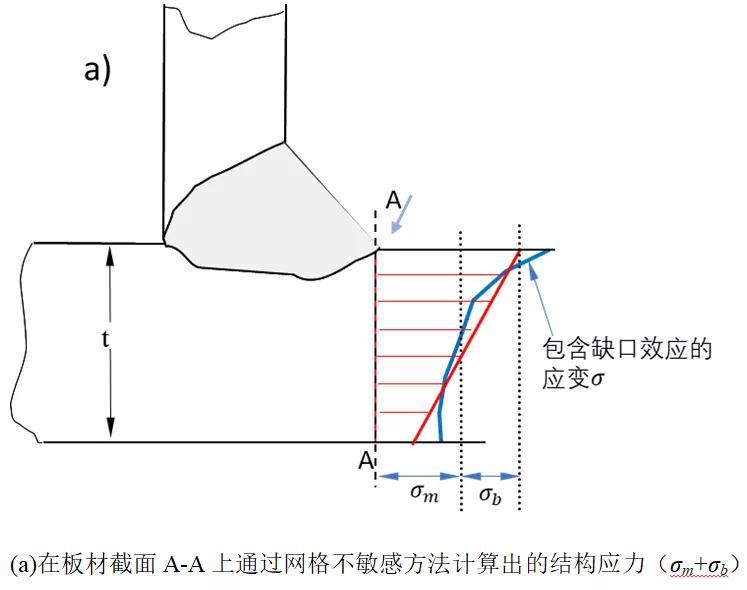
结构应力亦为广义应力,考虑结构宏观的几何特征引起的应力集中,但不考虑焊趾局部缺口效应。结构应力关注焊趾处的疲劳失效,其计算方法有表面外延法[14]、厚度线性化法[16]、E2S2法[17-18]以及1 mm法[19]等,学者Dong提出平衡等效结构应力计算方法,此方法满足力学平衡原理,实现有限元计算结果的网格不敏感性,为目前最准确、快捷的结构应力计算方法[17],承载截面上有正应力、剪应力,正应力包含膜应力σm和线性分布的弯曲应力σb,其中膜应力与外力的合力相平衡,弯曲应力与外力的合力矩平衡,剪应力亦满足力平衡关系,如下述公式所示,二维计算过程示意图参见图6。
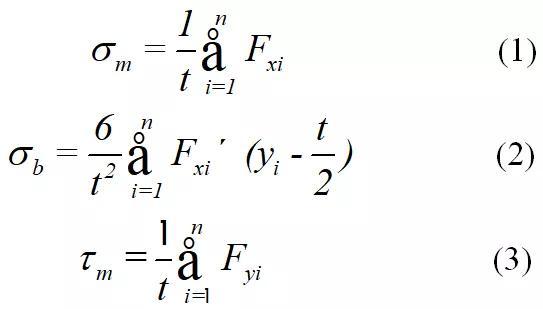
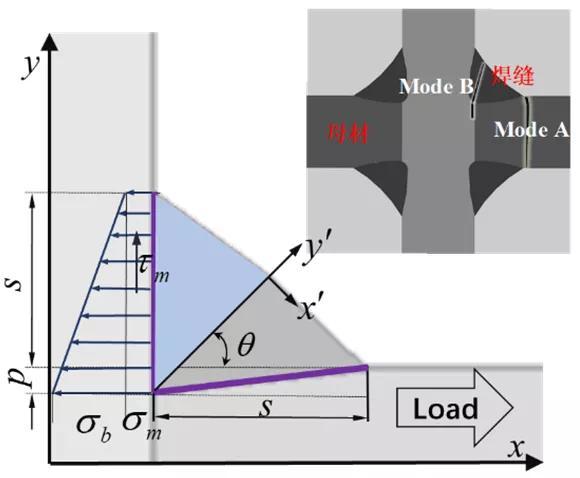
(a) 结构应力计算示意图
(b) 节点力提取路径示意图
图6 角焊缝中结构应力计算示意图[20]
3 Master E-N曲线与应用
董平沙教授在分析TWI等行业权威机构的S-N曲线疲劳试验数据发现,其斜率与裂纹扩展速率的乘积为-1,这意味着在焊接结构中疲劳寿命主要以裂纹扩展为主。这里并不是忽略裂纹萌生寿命,此部分作为焊接接头质量进行考察,体现为疲劳数据分散度。
焊接结构抗疲劳设计工作是解答:结构疲劳驱动力 vs 结构疲劳抗力,前者在上两节的工作基础上,还需要考虑裂纹扩展路径长度,以及载荷性质(正应力、弯曲应力、剪应力)的影响,后者多通过试验测试获得。
目前国际疲劳设计标准中根据不同材料、不同接头形式给出一组S-N曲线参照。试想如果可以准确计算结构的承载应力,那能否考虑将S-N曲线族变为一条S-N曲线,这必将大大的减缓设计难度,在新产品中不用担心无标准可依。
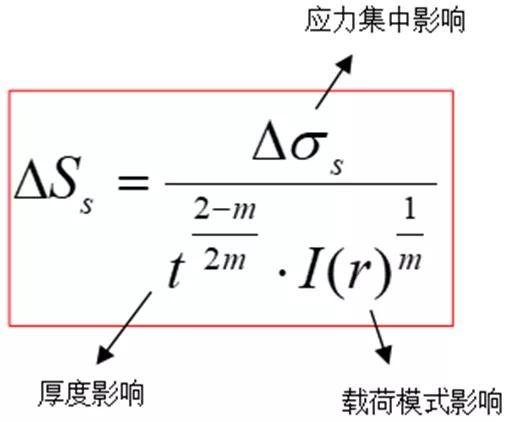
为实现上述想法,提出等效结构应力 (equilibrium-equivalent structural stress),这里equilibrium 指的是采用节点力或者线力计算时满足平衡条件,equivalent是在原有结构应力的基础上考虑板厚与载荷效应获得的新参量[30-31],这里t为裂纹扩展面的扩展路径长度,r为载荷比,I(r)为载荷修正量,无量纲。ASME Div. II在2007年将Master S-N曲线纳入其规范内,相关参量及含义此处不再赘述[31]。
(equilibrium-equivalent structural stress),这里equilibrium 指的是采用节点力或者线力计算时满足平衡条件,equivalent是在原有结构应力的基础上考虑板厚与载荷效应获得的新参量[30-31],这里t为裂纹扩展面的扩展路径长度,r为载荷比,I(r)为载荷修正量,无量纲。ASME Div. II在2007年将Master S-N曲线纳入其规范内,相关参量及含义此处不再赘述[31]。
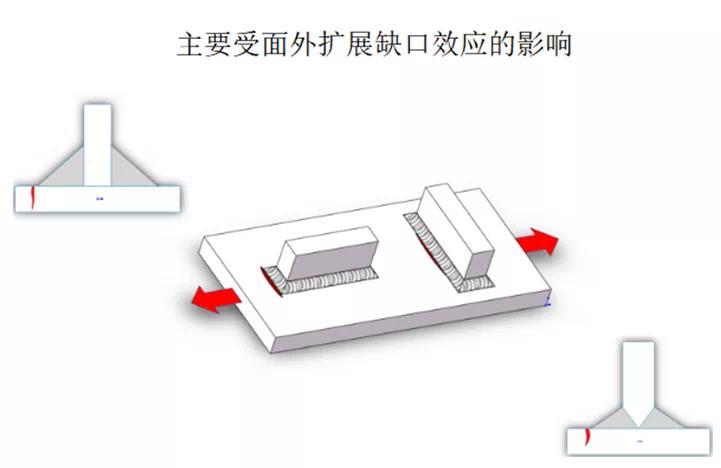
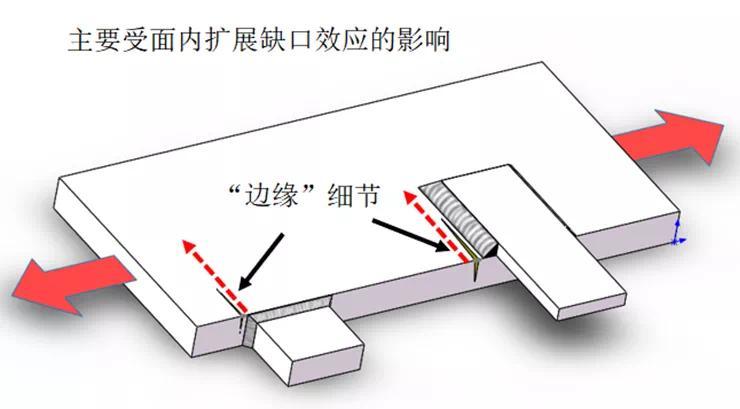
按照典型的裂纹扩展方式,可分为面内扩展(in plane)与面外扩展(out of plane),如图9中所示,面内扩展中板厚与实际板厚尺寸一致,但是面外板厚的取值需要分析疲劳试验中的刚度变化,经验认为刚度增加10%即裂纹达到临界尺寸,以满足此刚度要求的裂纹尺寸作为有效板厚尺寸。
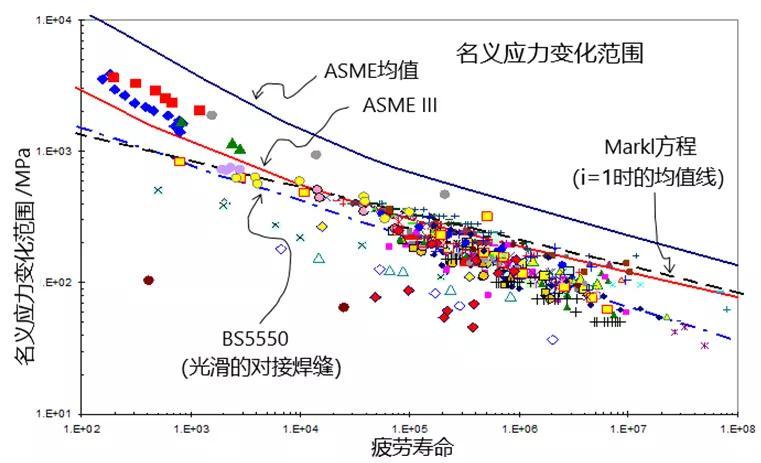
我们初步收集了来自英国标准BS5500,ASME III等权威标准验收通过的疲劳数据,这些数据的板厚范围为1.5-104 mm,包含对接接头、搭接接头、十字接头、带纵向加强筋试板、点焊接头多种接头形式,疲劳载荷类型包含:拉伸、弯曲及拉伸 弯曲组合加载,分别采用图10中名义应力下的S-N曲线与等效结构应力的S-N曲线进行对比,可以发现在名义应力表征时分散的疲劳数据带,当采用等效结构应力表征时,其S-N曲线基本上落在一个数据带中,因此称其为Master S-N 曲线。
图中局部数据点仍较为分散,分析原因是不同行业焊接接头质量差异所致,这里均为原始疲劳试验数据,由于缺乏具体试验细节,后续应加强有效试验数据的判据,使得数据更加科学性和合理性。
(a) 名义应力表征S-N曲线
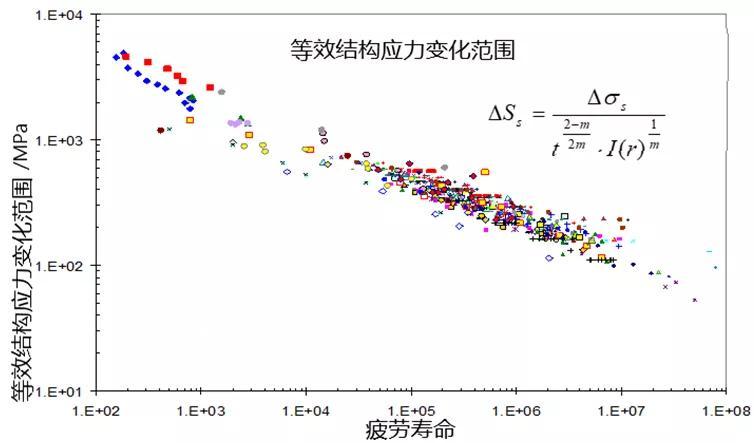
(b) 等效结构应力表征S-N曲线
基于节点力计算的结构应力法在2003年北美SAE FD&E “fatigue challenge”预测中空矩形梁的焊缝疲劳位置与疲劳寿命最为准确,因而被工业界接受[30]。2004年Ford Motor 在疲劳设计中采用此方法,2007年 ASME Sec VIII Div 2,API 579/ASME FFS-1采纳此方法,2013年法国船级社BV NT 3199开始推广此方法[32-34]。
结构应力方法虽然在焊接高周疲劳分析中有广泛的应用,但是往往在载荷控制的低周疲劳问题的处理上力不从心。主要因为接头在较大载荷下会发生宏观的塑性变形,此时虽然接头承担较大的位移载荷,但是接头截面的结构应力并不会明显增加,而是在材料的屈服强度附近变化。
因此直接采用结构应力方法 会大幅低估接头关键位置的应力。同时对于不同母材的焊接结构,在结构应力分析过程中,往往需要采用不同的S-N曲线,因而会给操作带来麻烦。因此用一条疲劳曲线来统一估计焊接结构的低周高周、以及不同母材接头的疲劳寿命是一个亟需解决的问题。目前轻量化制造使得异种材料的焊接需求大幅提升,更加速了上述需求。
在结构应力法基础上发展出来的结构应变法于是在上述使用背景下应运而生。结构应变法保留了结构应力方法网格不敏感性和Master S-N曲线的一致性,在结构应力分析的基础上,计算出接头关键位置的结构应变,进而可以通过一条Master E-N曲线来对低、高周疲劳及异种母材金属接头进行统一的疲劳分析。
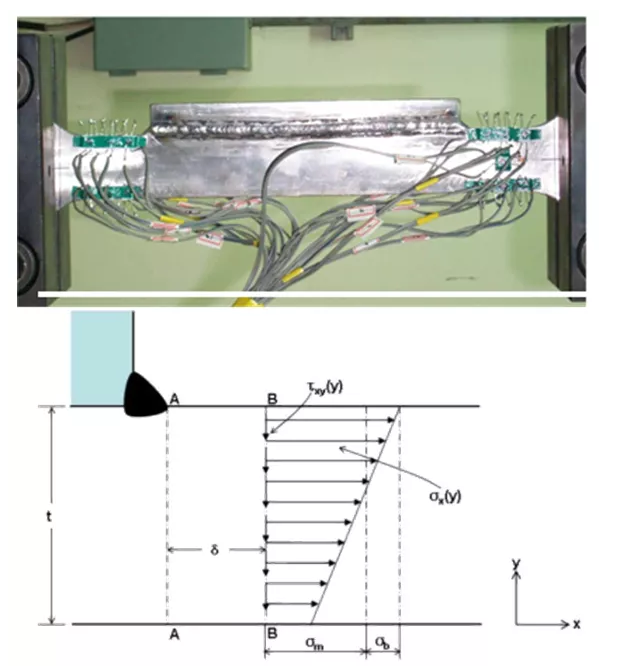
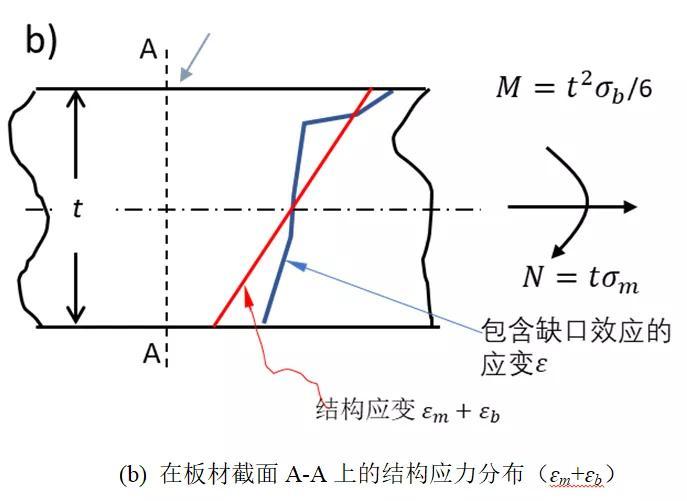
结构应变定义如图11所示。考虑如图中的板材焊接结构,由于焊接接头几何不连续造成的应力集中使得位于截面A-A的张开应力是高度非线性的,如图11(a)所示。然而该截面的结构应力则可以通过网格不敏感的方式计算得到,结构应力可分解为膜应力σm和弯曲应力σb。同理,该截面的局部应变也是非线性的,如图11(b)所示。结构应变在图11(b)被定义成等效截面在相同的结构应力σm σb作用下,产生的线性变形梯度,同样由膜分量ɛm和弯曲分量ɛb表征。
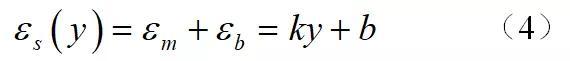
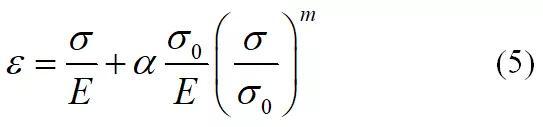
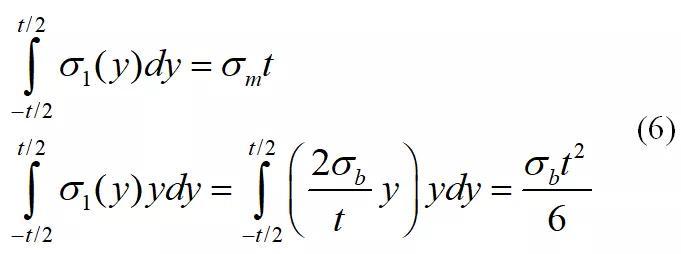
整个截面的应变梯度为线性分布,进而与结构应变的定义一致,可表达如下
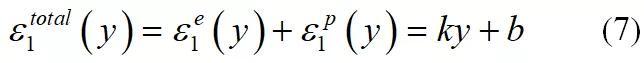
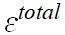 为截面的全应变,可以分解为弹性应变与塑性应变之和。钱令希院士在著作“余能原理”[41]一文中证明过即使在塑性变形下,梁截面的应力分布亦然满足上述线性形式。
为截面的全应变,可以分解为弹性应变与塑性应变之和。钱令希院士在著作“余能原理”[41]一文中证明过即使在塑性变形下,梁截面的应力分布亦然满足上述线性形式。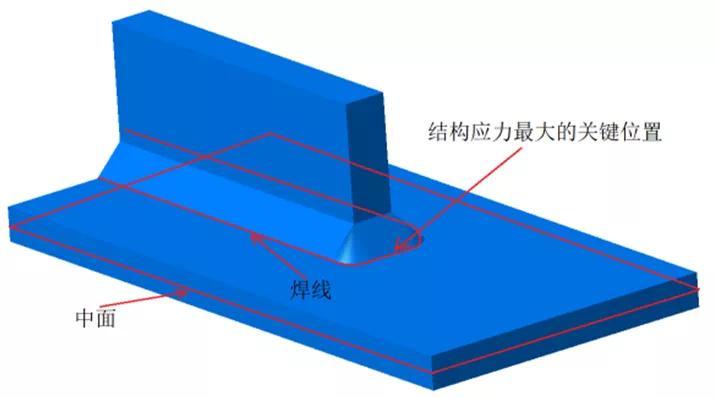
(a)受远端加载的筋板增强的板材焊接结构示意图
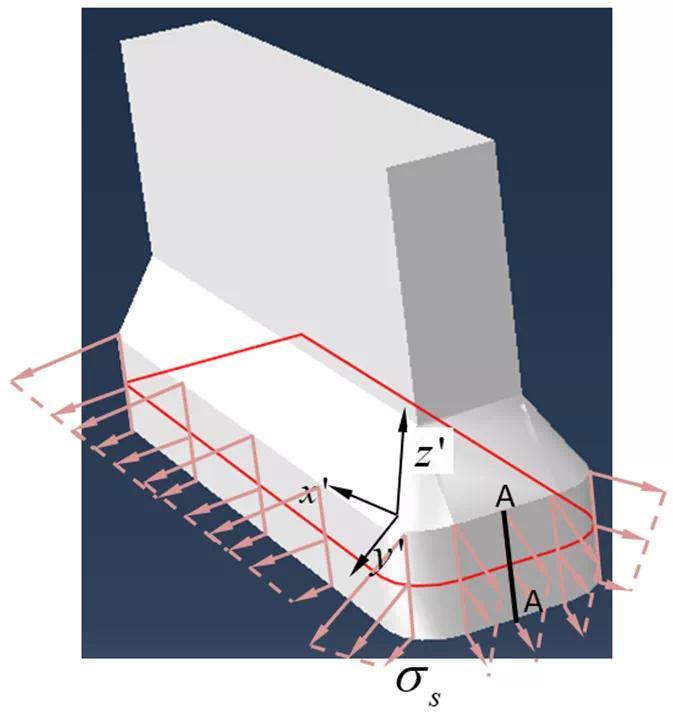
(b) 结构应力的计算
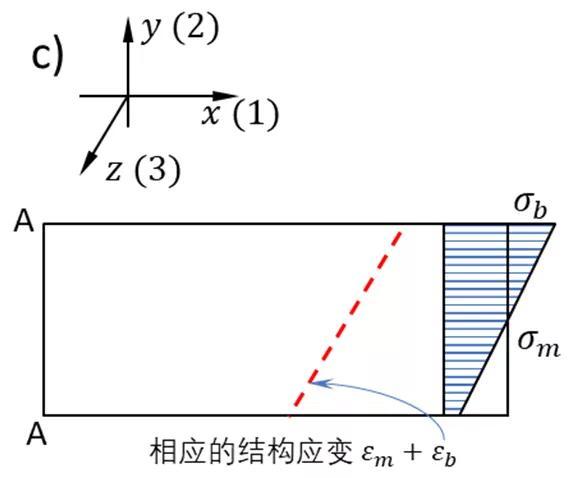
图12 筋板增强焊接接头计算示意图
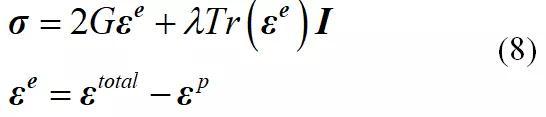
 是弹性应变的迹。G是材料的剪切模量。材料的拉梅常数 表达式如下
是弹性应变的迹。G是材料的剪切模量。材料的拉梅常数 表达式如下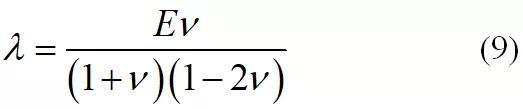
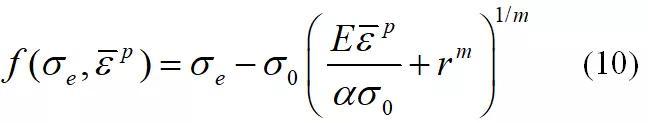
式中,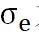 为米塞斯应力,
为米塞斯应力,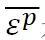 是材料的等效塑性应变。在计算塑性力学的框架下,材料屈服函数(10)应当时刻满足Kuhn-Tucker互补准则,即材料的屈服函数不能大于0
是材料的等效塑性应变。在计算塑性力学的框架下,材料屈服函数(10)应当时刻满足Kuhn-Tucker互补准则,即材料的屈服函数不能大于0
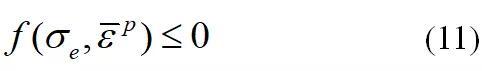
本研究采用塑性力学中广泛应用的关联流动法则,亦即,材料的塑性应变增量正比于屈服函数对应力张量的导数
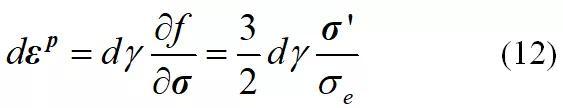
式中,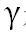 是塑性乘数,并且根据定义,
是塑性乘数,并且根据定义,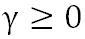 。并且在米塞斯屈服准则情况下材料的塑性应变增量可表达为:
。并且在米塞斯屈服准则情况下材料的塑性应变增量可表达为:
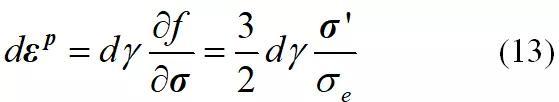
式中,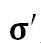 为偏应力张量。
为偏应力张量。
需要指出,根据公式(7),接头的结构应变由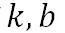 完全确定,因此只要提供一个可以有效求解(
完全确定,因此只要提供一个可以有效求解(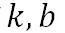 )的方法,使得(
)的方法,使得(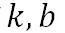 )满足由公式(6)-(13)所限定的条件。具体方法将在下一节展开。
)满足由公式(6)-(13)所限定的条件。具体方法将在下一节展开。
由于采用了非线性弹塑性模型以及考虑到平面应变约束,结构应变只能采用数值方法求解,具体求解的详细过程在[42]中给出。
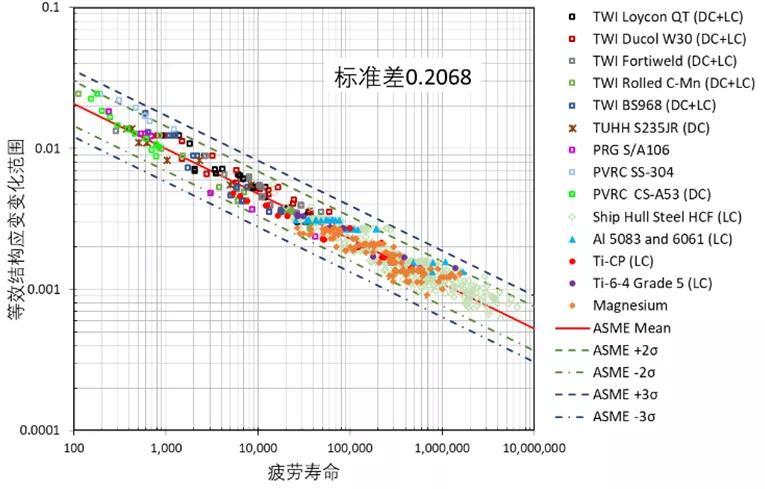
根据求解的结构应变结果,可以用类似图8所示公式计算等效结构应变
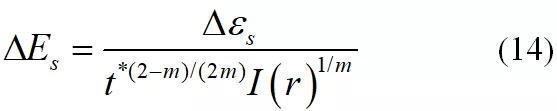
等效结构应变可以用来统一分析不同母材焊接接头高低周疲劳数据,结果如图13所示。分析数据包括不同型号的低合金高强钢、不锈钢、不同型号铝合金、钛合金疲劳数据。疲劳寿命从100周次到1000万周次。从图13中可以看出,结构应变方法是对结构应力方法的有效扩展,可以将结构应力方法应用范围推广到低周疲劳区域,并且用一条Master E-N曲线可以涵盖不同材质金属的接头疲劳行为。
4 焊接结构抗疲劳设计实例
上述章节中,将无网格敏感性的结构应力法及Master E-N曲线基本原理进行阐述,在抗疲劳设计中,此方法更适用于局部焊缝细节的设计与应用。
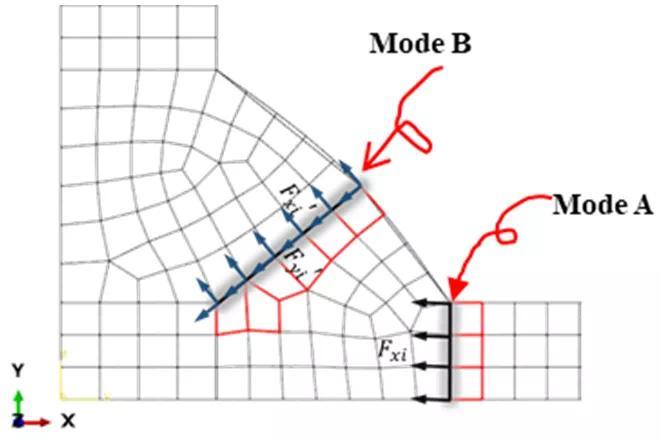
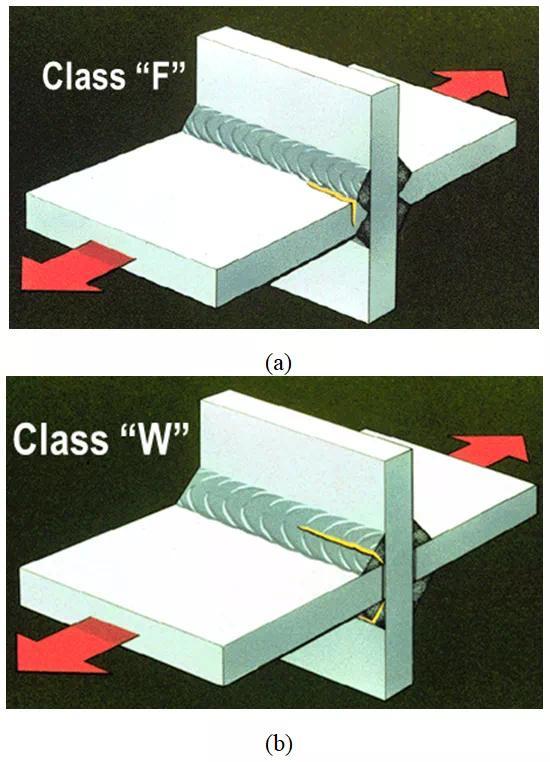
在焊接结构的疲劳特性中,我们提到抗疲劳设计满足的基本要求是焊趾失效,如图14(a)所示,然而设计标准中同时给出14(b)所示的焊根失效模式,并非现有设计标准考虑不足,在实际焊接过程中由于施焊可达性问题,往往更容易产生class W类型的接头。那么焊根未焊透问题如何解决呢?很明显增大焊缝尺寸效果最直接,然而如果无限大的增加焊接填充金属,会导致较大的焊接变形。合理的焊缝尺寸该如何设计呢?我们分析焊趾与焊根的受力状态,提出有效结构应力的计算方法[43-44]。
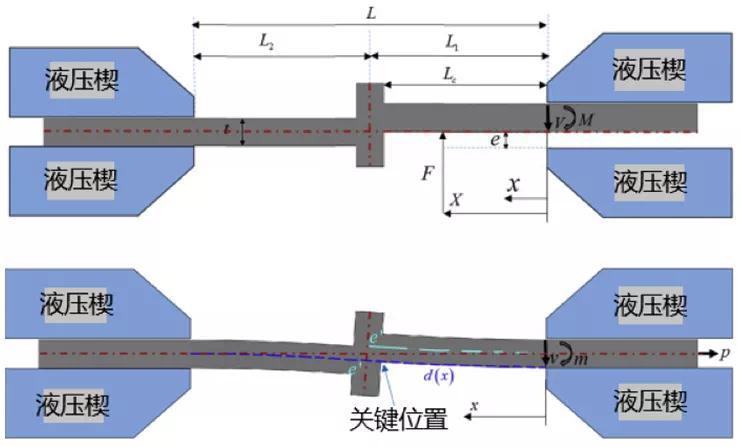
按照测试的十字焊接结构尺寸进行建模(图15),这里采用2D单元分析,由于此方法已被多次证实,2D与3D网格对结果影响很小,这里不再赘述。按照力、力矩平衡计算焊缝与焊趾处的膜应力、弯曲应力,公式如(15)、(16)
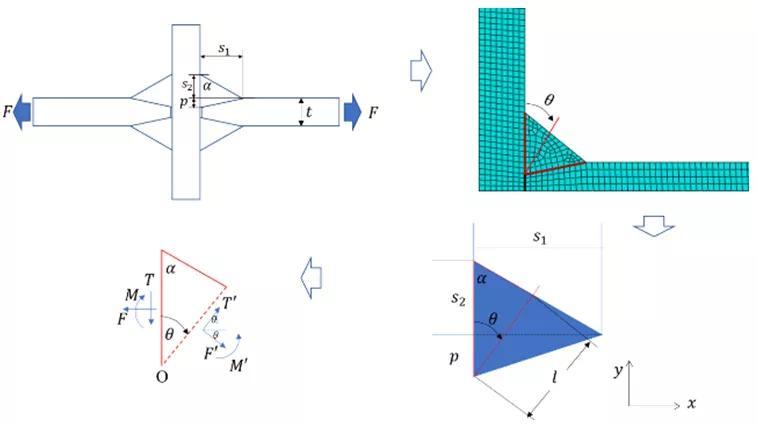
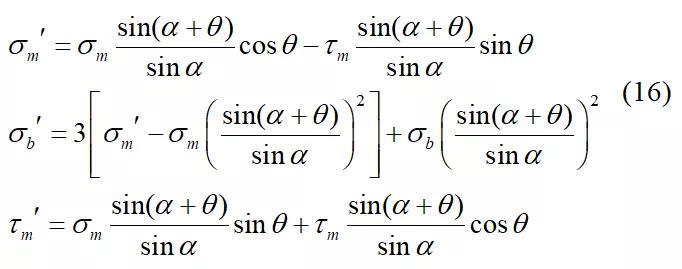
提出有效结构应力(effective traction stress/ETS) σe(θ)
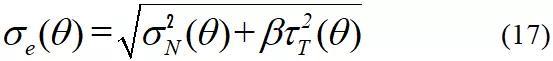
式中,参照Mises应力定义,令β=3;σN为裂纹面上的正应力分量,τT为裂纹面上的剪应力分量。
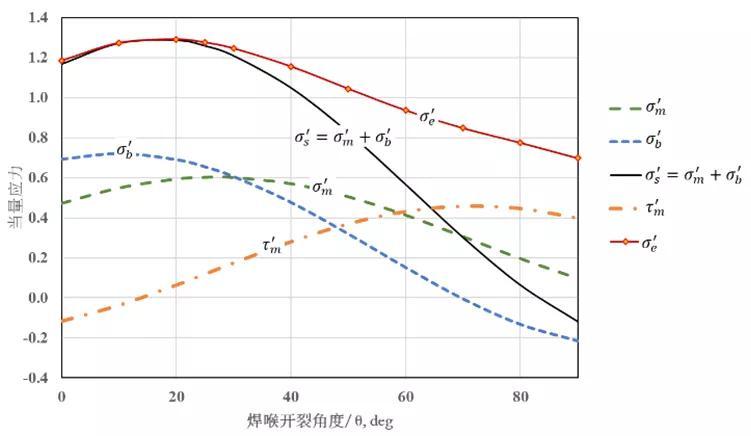
当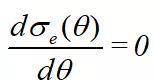 时,有效结构应力达到极值,此时θ即为焊喉的开裂角度,即焊喉的裂纹面。分析可以发现,对于熔透率为零的角焊缝而言,焊喉开裂的角度不是传统中的45°,而是接近20°,如图16所示。对比这里断裂面上等效结构应力与焊趾所在截面的等效结构应力,即可获得此接头的失效模式,在此基础上,可增加焊缝尺寸或者增加熔透率实现接头失效模式的转换。
时,有效结构应力达到极值,此时θ即为焊喉的开裂角度,即焊喉的裂纹面。分析可以发现,对于熔透率为零的角焊缝而言,焊喉开裂的角度不是传统中的45°,而是接近20°,如图16所示。对比这里断裂面上等效结构应力与焊趾所在截面的等效结构应力,即可获得此接头的失效模式,在此基础上,可增加焊缝尺寸或者增加熔透率实现接头失效模式的转换。
十字接头疲劳试验中,通过线切割焊缝根部金属,获得不同的熔透率,增加熔透率相当于增加焊喉的有效裂纹长度,因而可实现失效模式的转换,参见图17,当熔透率高于40%时,铝合金十字接头在焊趾处失效,满足抗疲劳设计要求。

焊接产生的错边、角变形等会影响结构的疲劳性能。错边仅仅影响焊趾疲劳性能,在焊趾处产生附加弯矩,降低其疲劳抗力,图18所示。角变形的影响要远小于错边缺陷[45]。通过测试十字接头的错标、角变形,并分析给出解析计算公式,发现采用结构应力法分析焊接变形的影响比现有标准BS7910准确适用。
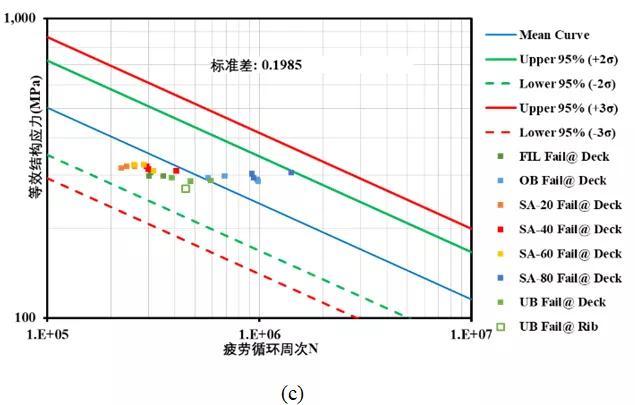
我国现在桥梁建设体量与速度位于世界前列,正交异性桥的疲劳问题备受关注,成为国内外学者研究的热点。正交异性桥面板为大型结构相关的疲劳试验费时费力,迫切需要在行业内建立统一的设计标准,Master S-N曲线满足这一要求。2019年我们采用此方法对上海交通大学与美国ASSHTO的疲劳试验数据进行分析,使用结构应力法计算潜在4种疲劳开裂位置(桥面板焊趾、桥面板焊根、U肋骨焊趾、U肋骨焊根),参见图19,并根据加载条件的不同进行分析,发现其疲劳试验数据均在Master S-N曲线的标准差带中,而且数据分散度最小。