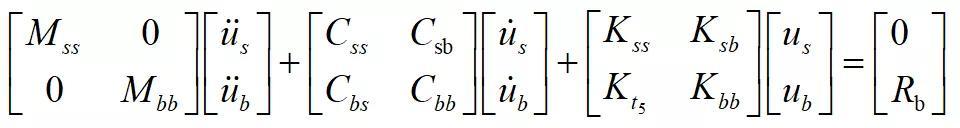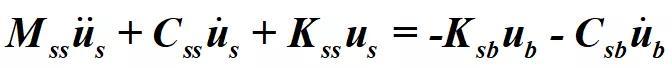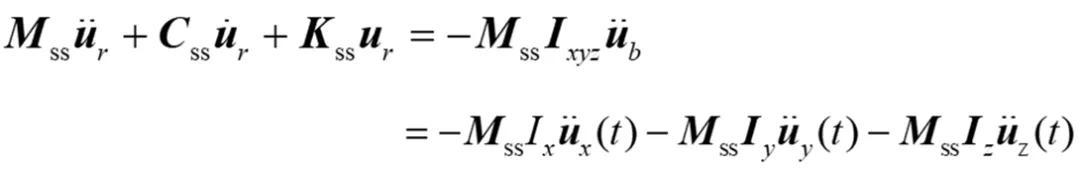建筑结构抗震分析之施加地震波的方法与理论机理


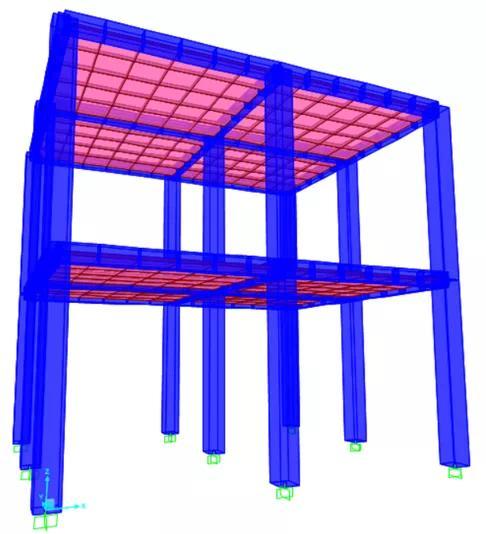
建筑结构抗震分析中,动力时程分析方法是最常见的分析方法之一。最近有人问在软件中施加地震波应该怎么加?其实,在对结构模型进行地震时程分析时,最常见的方式有三种方式。

在大部分软件中,采用的是第一、二种方式进行加载,而对于少部分软件也可采用第三种方式进行施加,具体如图所示。
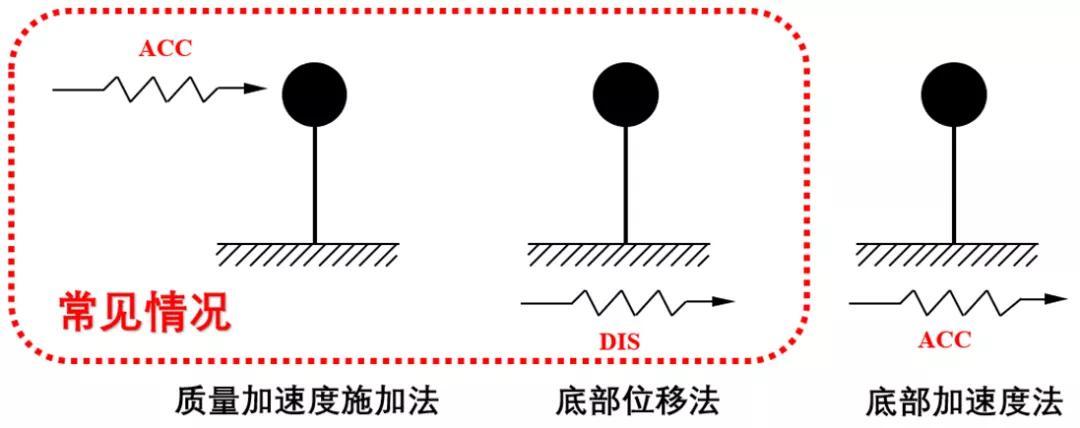
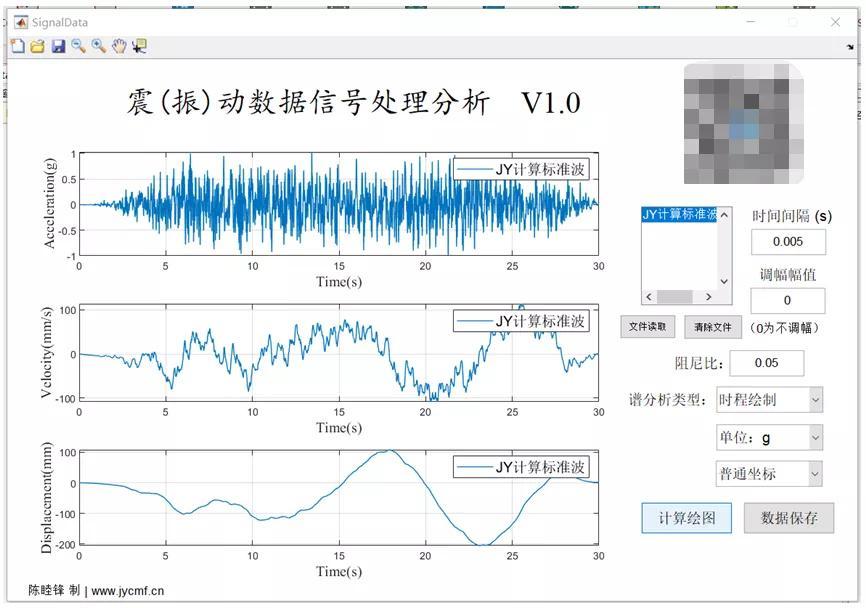
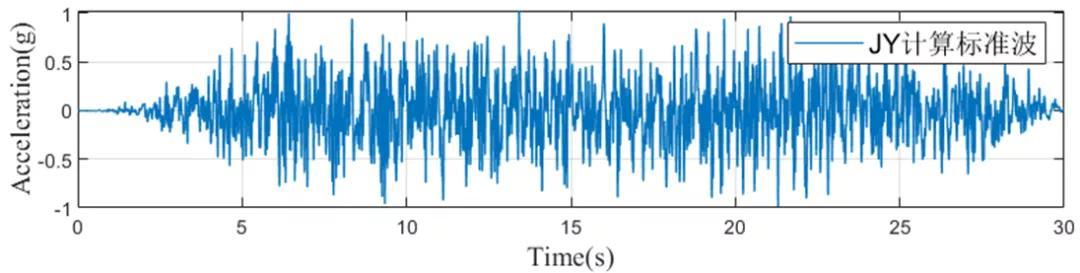
对于施加加速度或者位移,通常我们可以收集得到相关的地震动加速度,首先将地震动加速度进行转换得到位移,可采用自编的SignalData软件进行转换。
质量加速度法,在模型中施加地震波:
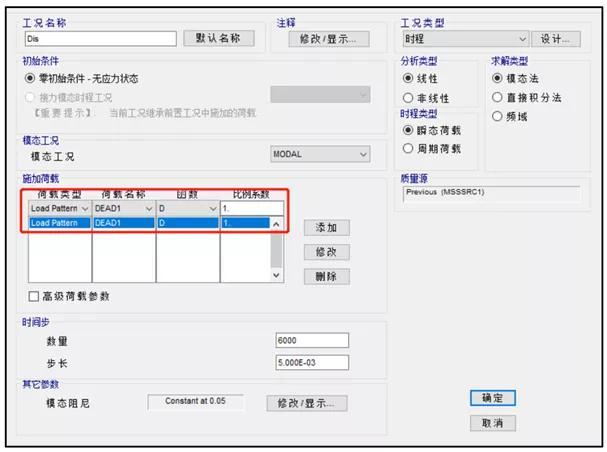
SAP2000软件中质量加速度施加法工况如图所示:
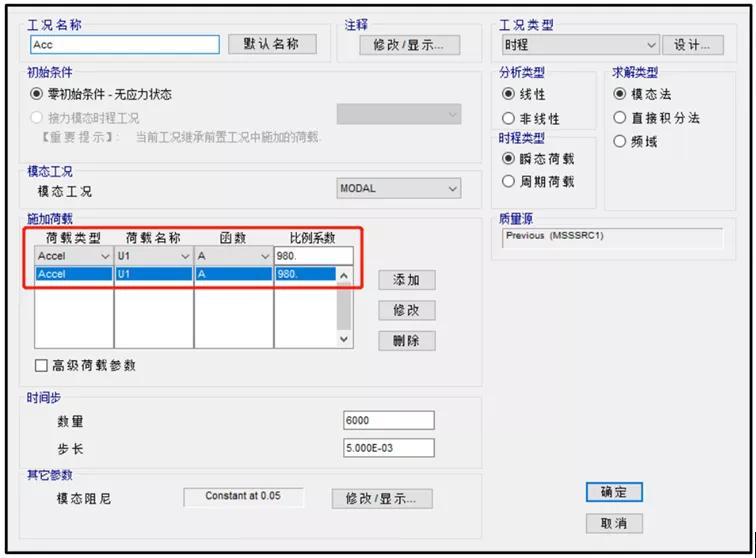
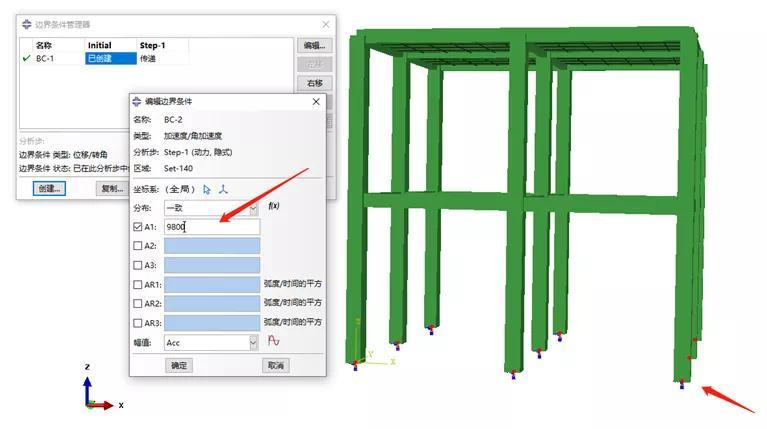
底部位移法,在模型中施加地面位移,不过需要施加支座单位1的位移:
SAP2000两种质量加速度施加法、底部位移法中结构顶部节点绝对加速度对比:SAP2000两种施加方法质量加速度施加法、底部位移法中结构顶部节点相对位移对比:
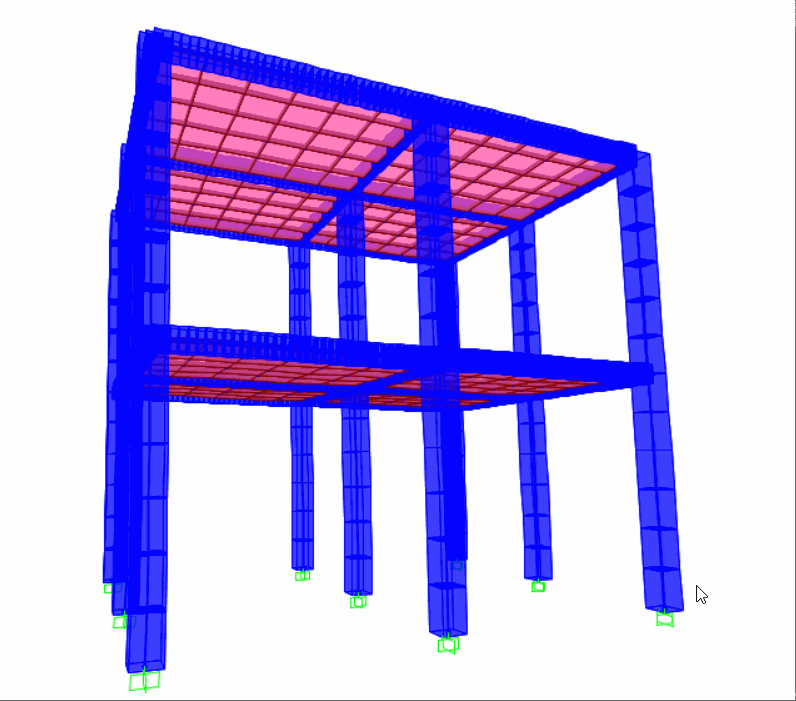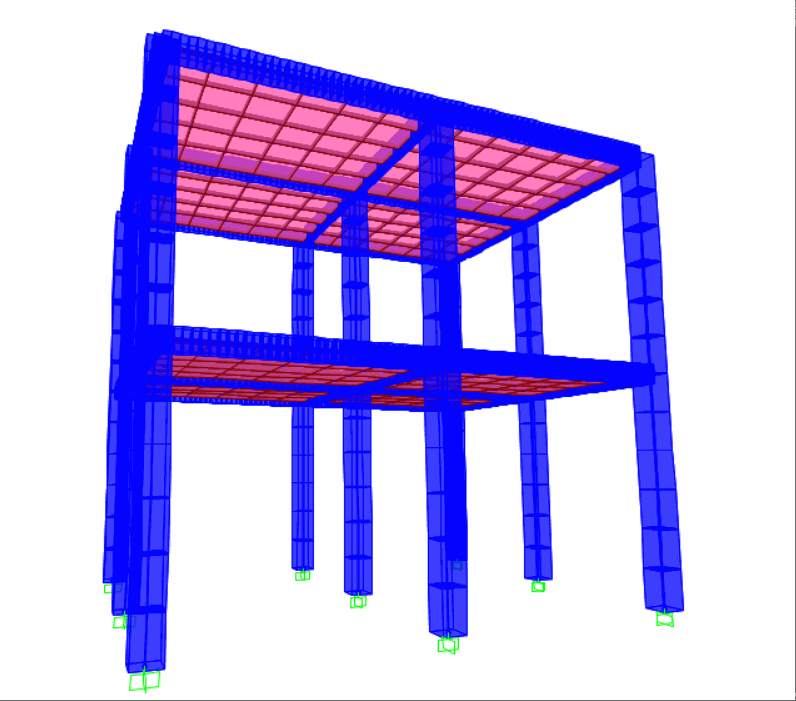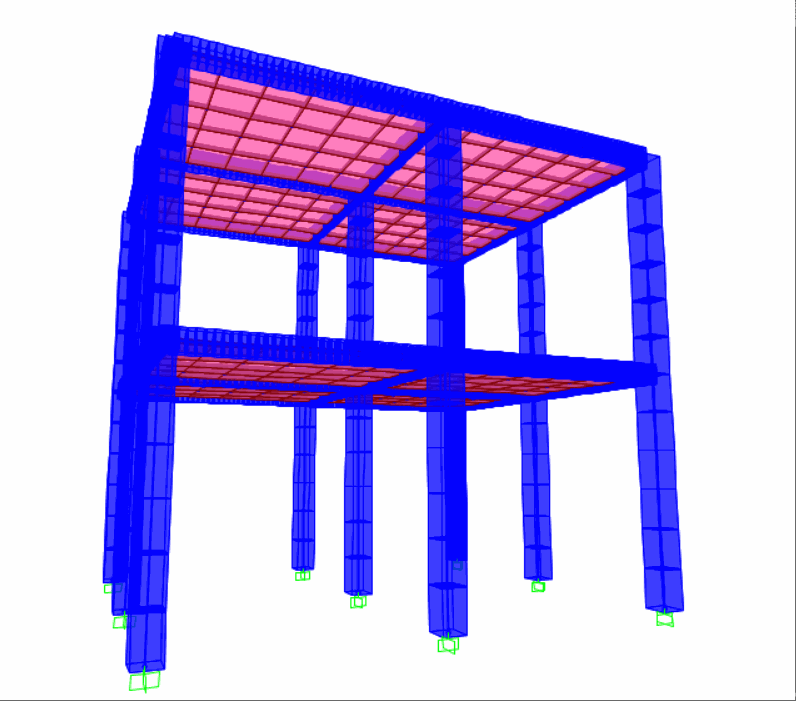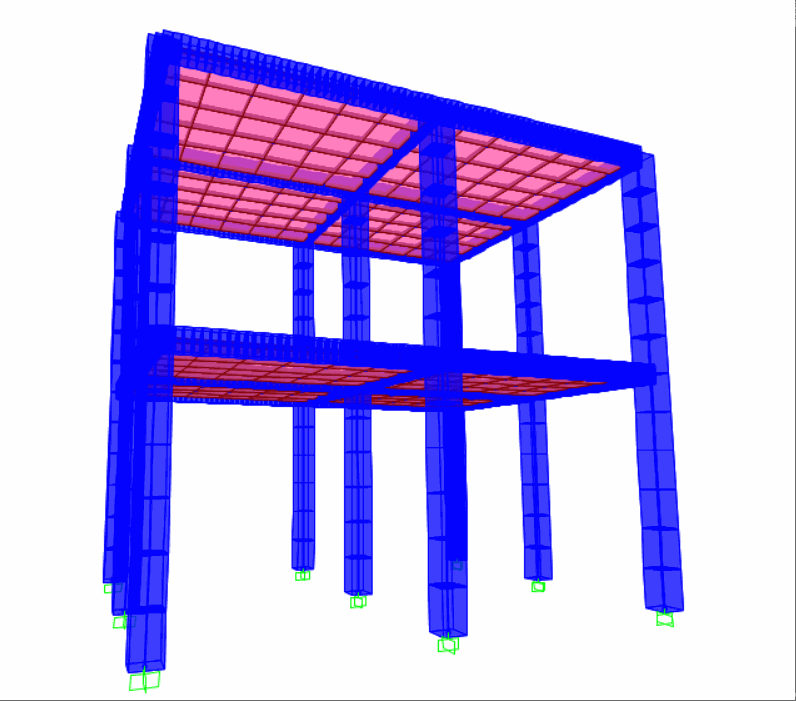
SAP2000质量加速度施加法
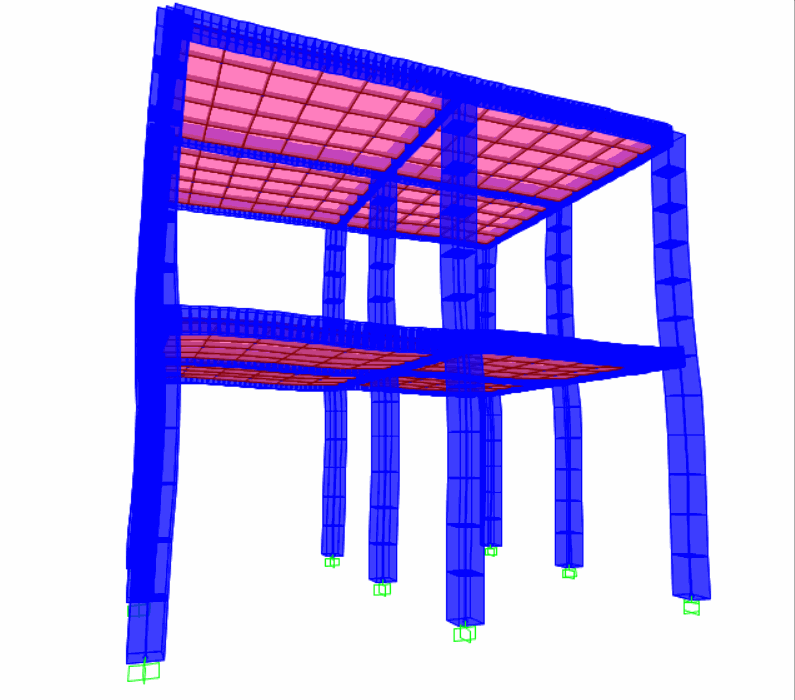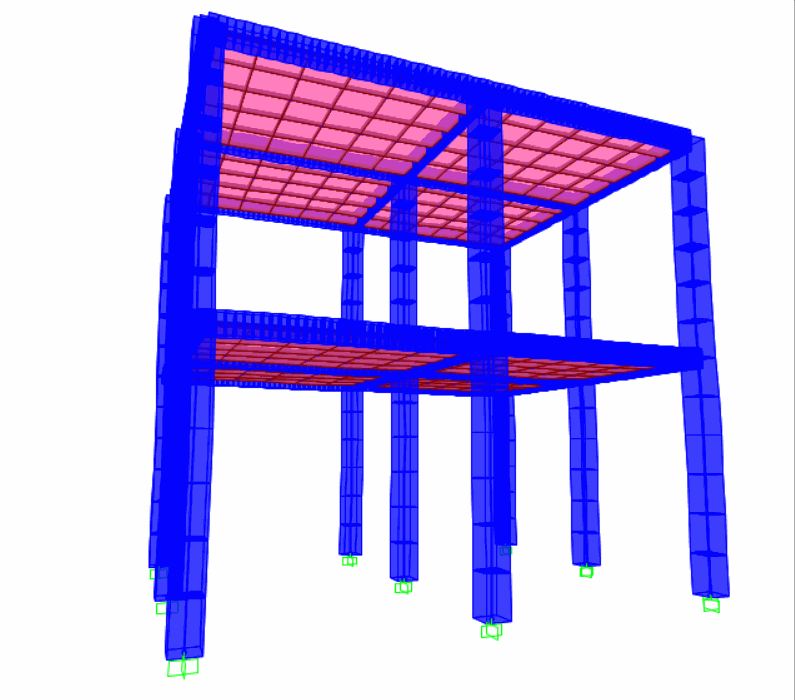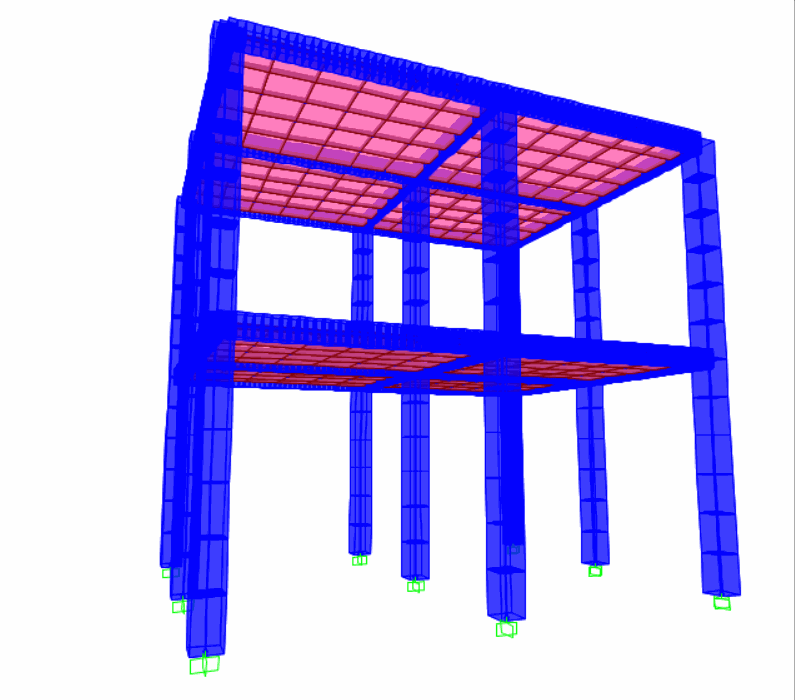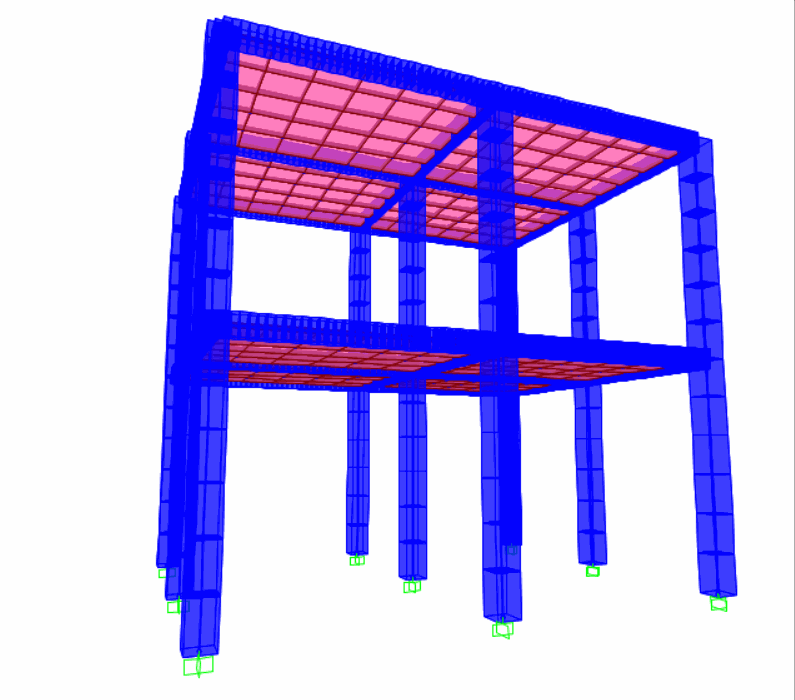
质量加速度施加法(在结构质量上施加加速度荷载);
底部加速度法(以地面加速度方式施加与结构底部);
底部位移法(以地面位移方式施加与结构底部);
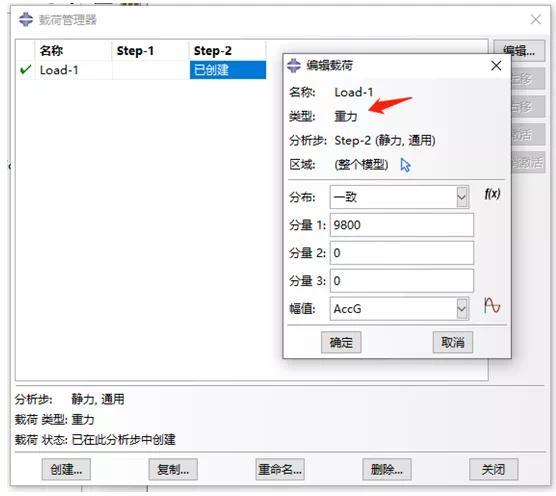
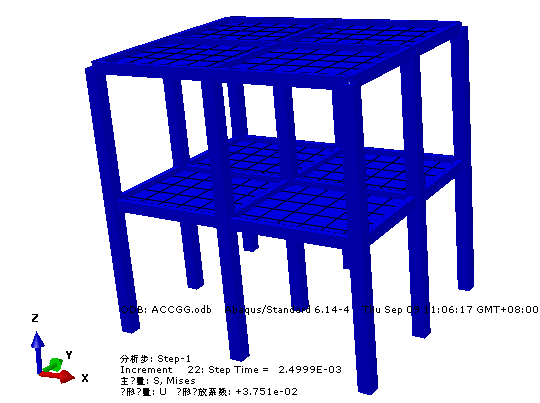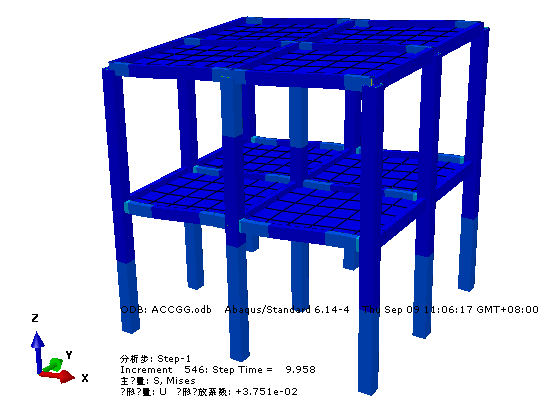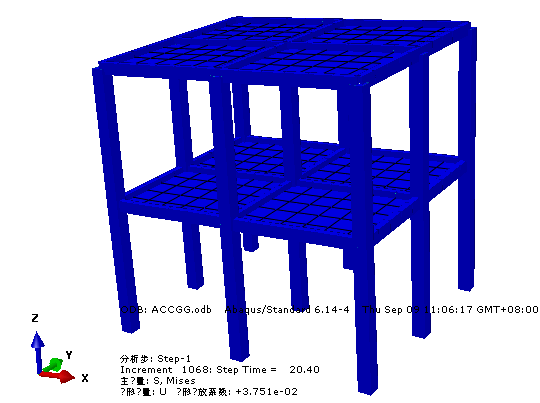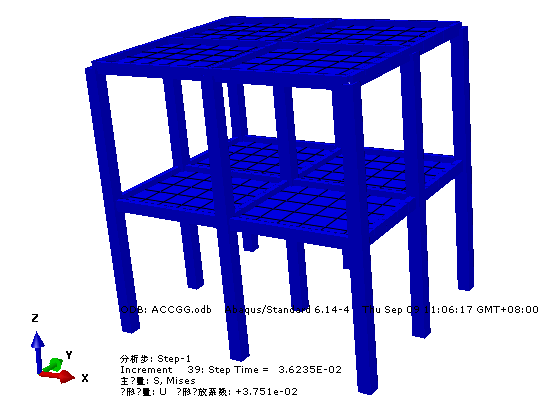
ABAQUS软件中质量加速度施加法施加方式如图所示:
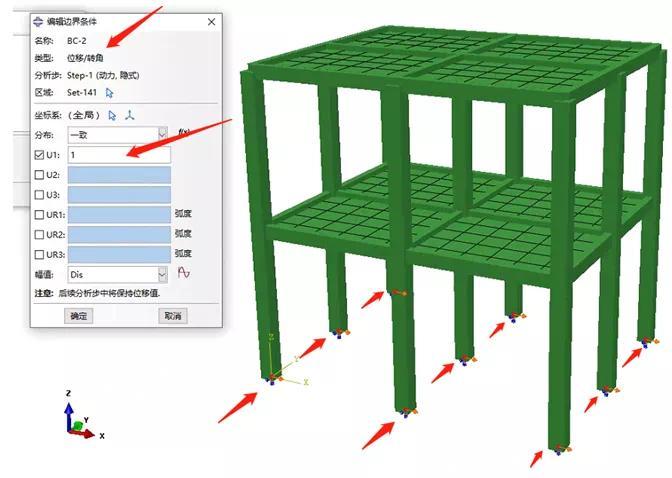
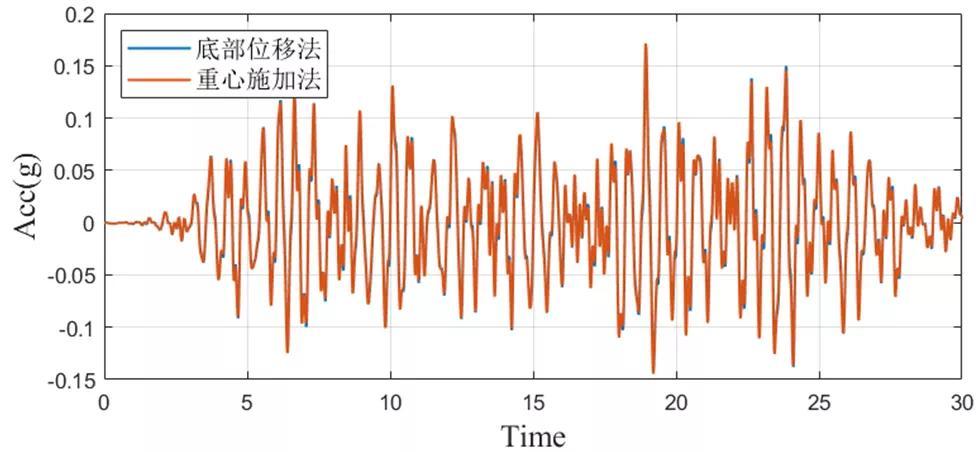
ABAQUS三种施加方法重心施加法、底部加速度法、底部位移法中结构顶部绝对位移对比:
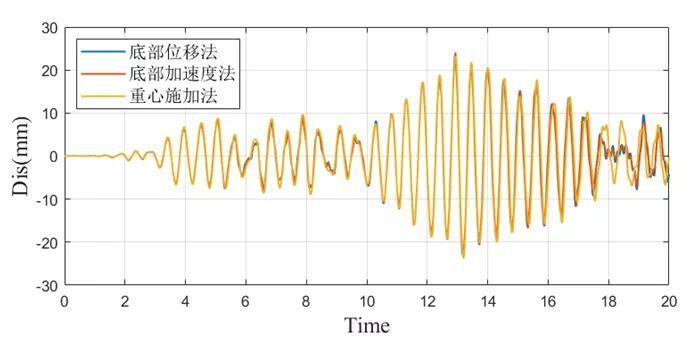

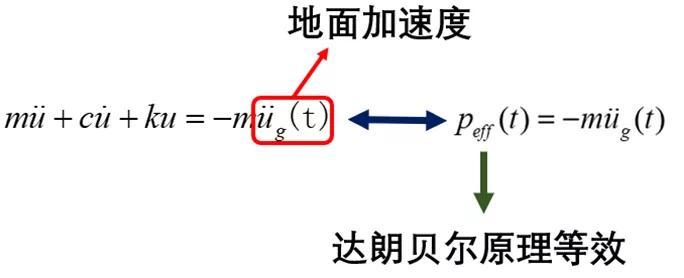
从以上结果对比分析,三种不同的加载方式最后的结构响应结果几乎一致,其中底部施加法的原理都是底部位移施加,不论是底部加速度还是底部位移法;在ABAQUS中,用的是直接积分法HHT法,质量加速度施加法的计算效率高于底部施加法,具体请继续往下看。达朗贝尔原理(D'Alembert's principle)是求解约束系统动力学问题的一个普遍原理。达朗贝尔原理表明,结构分别承受两种激励(地面加速度和外力)的运动方程相同。这样,由于地面加速度产生的结构相对位移(或变形)u(t) 将与地基不动并承受外力作用产生的结构位移 u(t) 相同。因此结构分别承受两种激励(地面加速度和外力)的运动方程相同。该力等于质量与地面加速度的乘积,方向与加速度方向相反。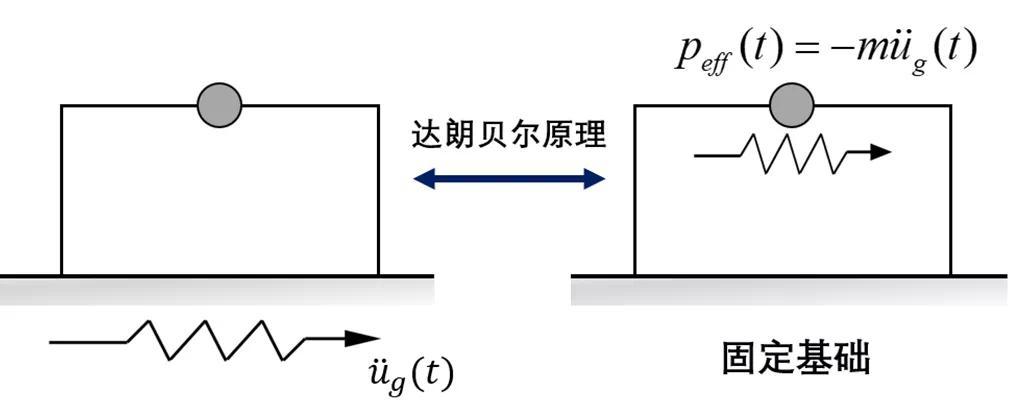
在结构承受随时间变化的支座移动时,结构的反应来源有两部分:1、支座移动引起的结构反应,称为拟静力反应;
2、支座移动加速度导致的惯性力引起的结构反应,称为动力反应。对于一个集中质量系统,动力平衡方程用上部结构内未知的节点位移us和基底节点指定绝对位移ub形式可写为:
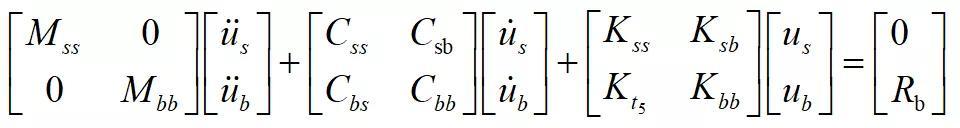
与这些位移相关的质量、阻尼和刚度矩阵由M、C、K指定。注意与指定位移相关的力Rb是未知的,并且可在计算出us之后得到。从上面方程,只对上部结构的平衡方程按在基底节点指定的绝对位移可写做:将待求的相对地面的节点位移us进行变换,得到包含地面位移的节点绝对位移ur,可得到下列方程。由于与结构刚体 位移相关的力为零,实际的阻尼矩阵几乎不可定义,所以在方程右边的阻尼力通常被忽略。
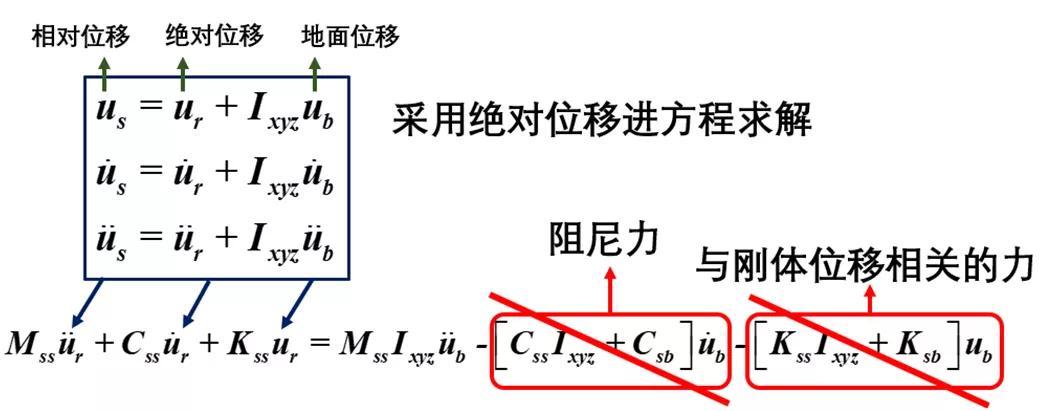
因此,以相对位移形式的三维动力平衡方程,通常写为下面近似形式:通过对上述方程进行动力求解,再进行绝对与相对值的变换,可得到所需的结果。注意相对位移公式中的荷载空间分布与方向质量成正比。当位移在结构内传播时,该类型点荷载空间分布将激发系统的高频振型。如果指定了完全阻尼矩阵而且在上述方程中的右边包含了阻尼项,绝对和相对公式的精确解。因此可以看到是采用位移加载时,可使得底部节点分别得到不同的位移,及该方法适用于多点激励。
事实上,结构真正承受的是地震位移,只是地震加速度更容易测试得到,不过即便是施加位移,该方法最终转换为加速度进行计算分析。因此在上述的三种方法的计算效率为:
质量加速度施加法 > 底部加速度施加法 > 底部位移施加法
以上就是笔者关于结构中如何施加地震波软件实操技能和理论总结,在仿真秀土木工程有限元分析学习月来临之际,9月22日20时,笔者将作为嘉宾给大家带来《建筑结构(震)振动控制与仿真分析入门》公开课。讲课安排如下:

本文课程相关模型和资料,请点击文章附件下载即可,如下图:作者:建源之光,工学博士,结构工程-结构振动控制方向研究。高级技术经理,自主研发软著 4 项,专利 21 项。主要从事超高层建筑结构设计分析,减隔震设计分析,舒适度及其他振动控制分析,减隔震(振)元件设计开发。建源学堂,土木与有限元优质内容创作者,超高层建筑结构设计分析,减隔震设计分析,舒适度及其他振动控制分析,Sap2000,Etabas,Abaqus,Matlab,OpenSeespy。声明:原创作品,首发仿真秀App,部分图片和内容源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。获赞 10732粉丝 22226文章 3773课程 233