最大/最小实体要求的本质是什么
本文摘要(由AI生成):
本文介绍了两种机械领域的批量制造方法:配做和互换性装配,并重点阐述了最大实体要求和最小实体要求的概念和应用。最大实体要求用于保证零件装配无干涉,而最小实体要求则适用于毛坯件和成品件的关系,保证加工余量和最小壁厚等要求。通过引入生活实例,文章让读者更容易理解这些概念,并强调了它们在实际应用中的重要性。最后,文章鼓励读者多看几遍并结合实际案例或生活常识加深理解。
看到这个标题,手机面前的你有没有虎躯一震的感觉,不知道有多少朋友在它们面前折戟沉沙一蹶不振,也有不少小伙伴摩掌擦拳跃跃欲试。说到底还是因为这两个知识点在GD&T/GPS的学习中占据了C位,也是整个公差体系的精华所在。美好的东西总是没那么容易被征服,所以大家可以耐心一点,只要过了这一关,你会发现面前豁然开朗,很多知识点就可以自然地融汇贯通,那感觉不要太惬意。
好了,言归正传。在研究这两个要求之前,得先了解几个概念
最大实体状态MMC(Maximum Material Condition):
一个FOS在其公差允许范围内使零件拥有最多材料的状态。比如直径处于公差下限的孔,或者直径处于公差上限的轴。
我们可以想象,材料最多的状态下,该FOS的截面形状一定是理想的(即形状公差为0)且处处相等。但需要注意的是,最大实体状态本质上只是对该FOS处于最大体积状态的描述,而与要素的整体形位公差无关。如下图例子所示,轴和孔的整体形状可以是弯曲的,但只要处于最大实体状态,其体积总是不变的
最大实体尺寸MMS(Maximum Material Size):
最大实体状态对应的相应尺寸值,如下图中的Φ50.2孔径和Φ49.8轴径
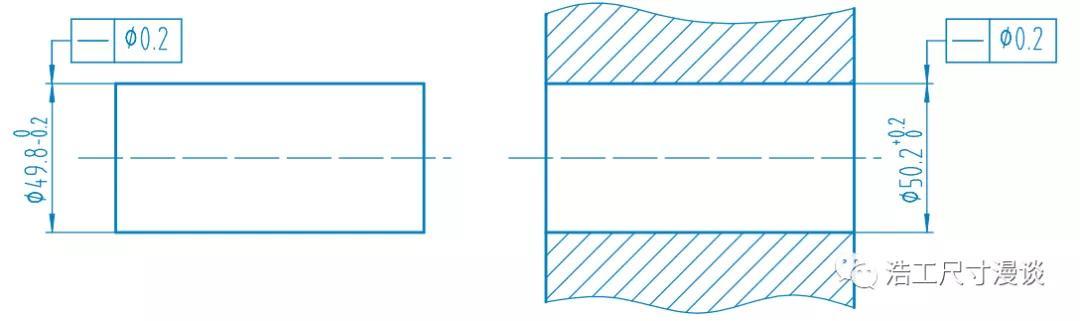
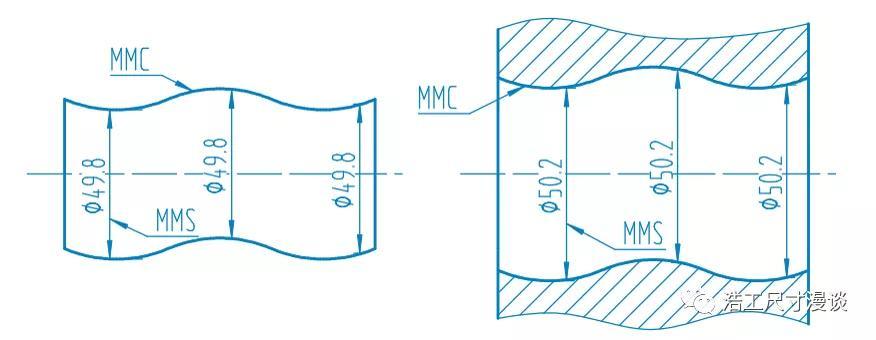
最小实体状态LMC(Least Material Condition):
一个FOS在其公差允许范围内使零件拥有最少材料的状态。比如直径处于公差上限的孔,或者直径处于公差下限的轴
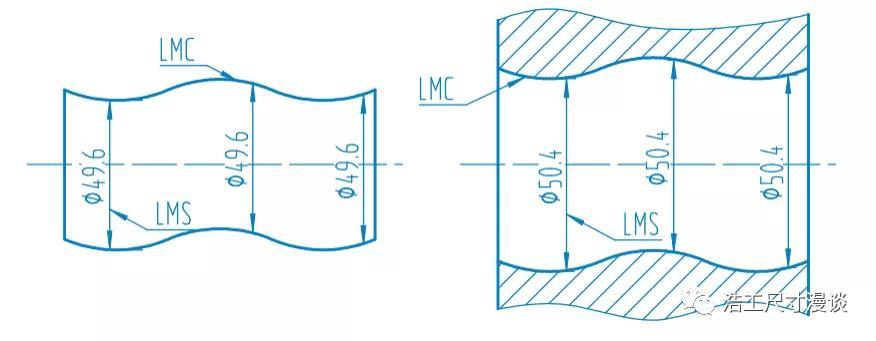
最小实体尺寸LMS(Least Material Size):
最小实体状态对应的相应尺寸值,如下图中的Φ50.4孔径和Φ49.6轴径

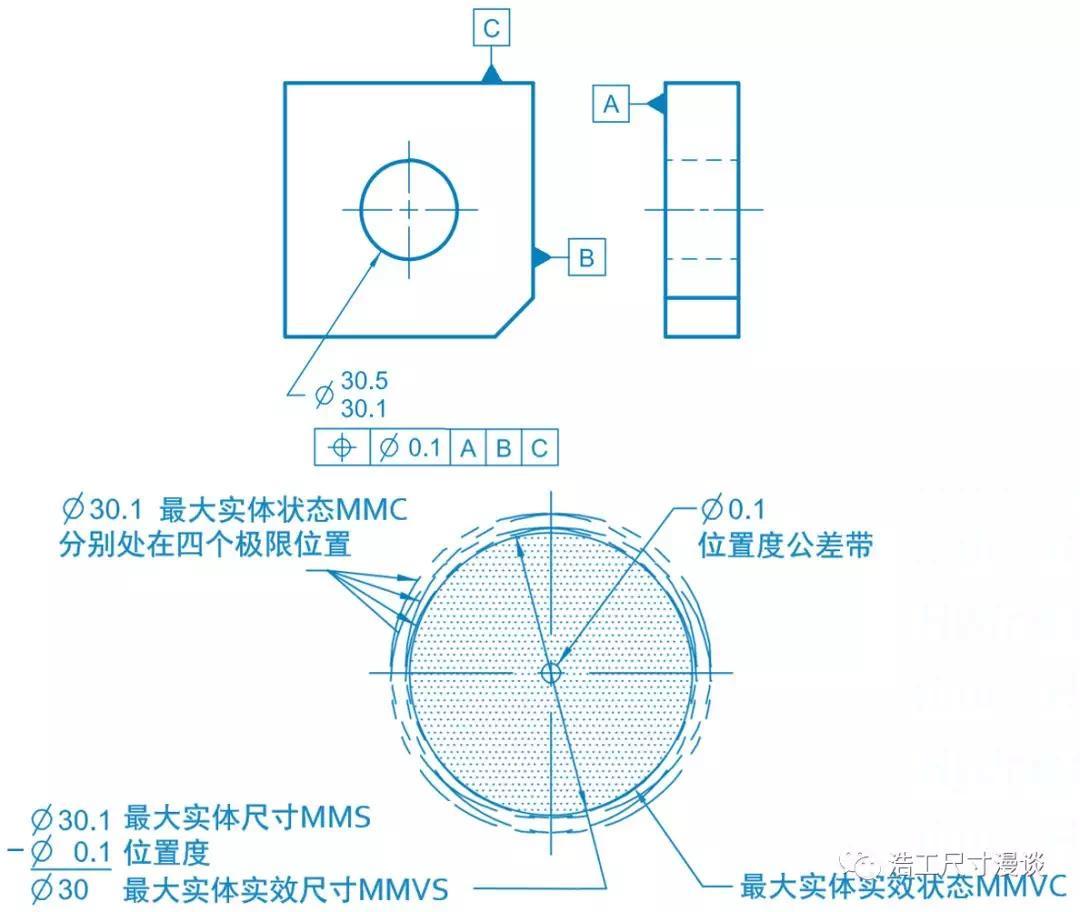
最大实体实效状态MMVC(Maximum Material Virtual Condition):
一个FOS处于最大实体状态时在允许的形位公差范围内自由变形或移动所形成的体外包络边界所构成的虚拟形体。
我们在之前的文章中介绍过,FOS的一大特征是存在中心要素,比如轴线,中面等,而这里说的形位公差主要就是中心要素的形位公差(因为上面提到在最大/最小实体状态下截面的形状公差一定为0)。接下来可以这样来理解,如果我们能已知中心要素的形位公差带,然后让中心要素在这个公差带内任意移动,这时整个尺寸要素的表面也会随之移动,那么在无数次随机移动后会形成一个体外边界(最大实体实效边界),我们可以想像到这个边界也将是一个理想形体,这种状态即是所谓的最大实体实效状态。
最大实体实效尺寸MMVS(Maximum Material Virtual Condition):
最大实体实效状态对应的理想形体的尺寸。
对于外部FOS,如板,轴等
MMVS=MMS 中心要素形位公差
对于内部FOS,如孔,槽等
MMVS=MMS-中心要素形位公差
最小实体实效状态LMVC(Least Material Virtual Condition):
一个FOS处于最小实体状态时在允许的形位公差范围内自由变形或移动所形成的体内包络边界所构成的虚拟形体。
最小实体实效尺寸LMVS(Least Material Virtual Condition):
最小实体实效状态对应的理想形体的尺寸。
对于外部FOS,如板,轴等
LMVS=LMS-中心要素形位公差
对于内部FOS,如孔,槽等
LMVS=LMS 中心要素形位公差
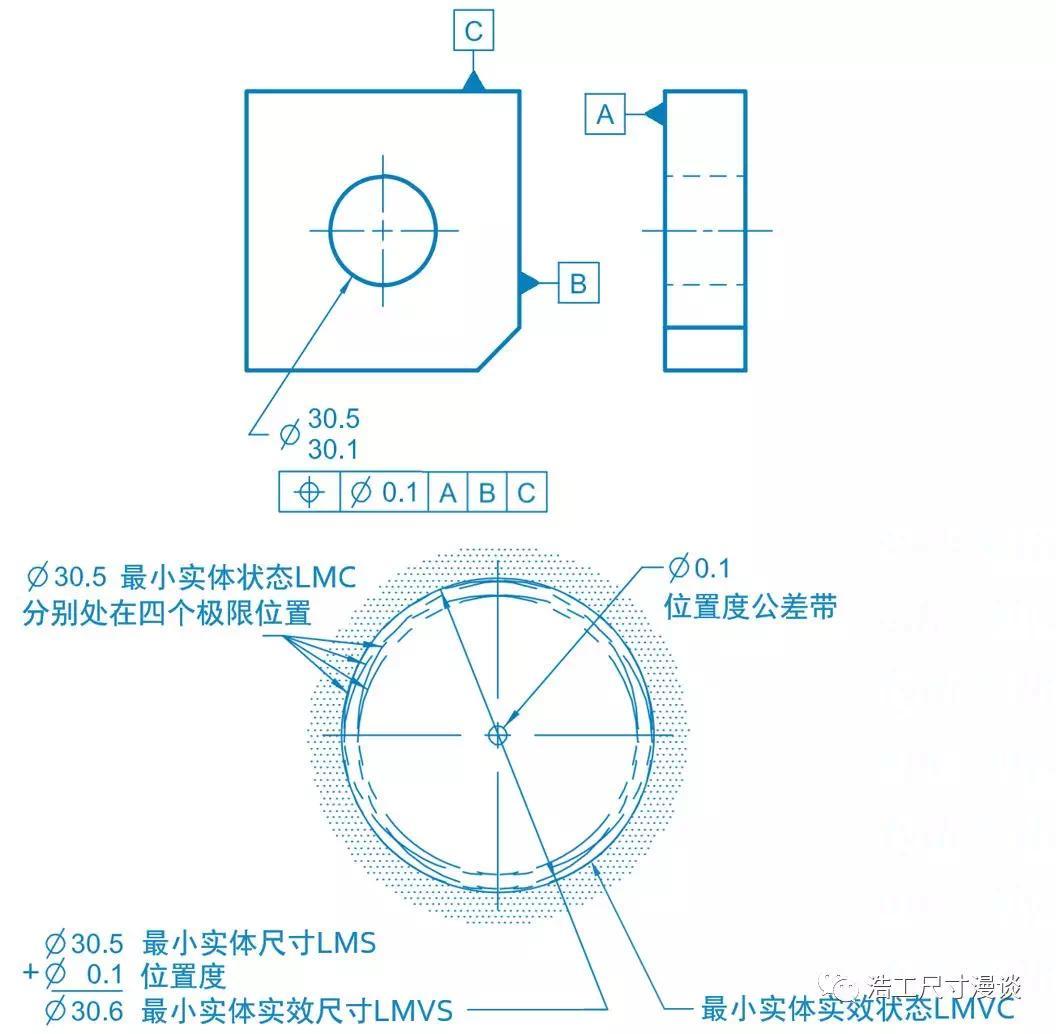
好,聊到这里,我们来思考一下GD&T/GPS为什么要创造出这些概念。
先以最大实体为例,我们之前反复提过,GD&T/GPS的一大重要作用是保证装配,而装配中90%是间隙装配,也就是说相配合的两个零件不能有干涉。
怎么实现呢?咱们来从生活中的例子寻找点灵感。相信大家在小时候上学时都经历过与同桌的桌面空间争夺战,要么你的书压了他的笔,要么他的胳膊把你的本子杵跑了,这就是你们各自的势力范围发生了干涉,这时你们有两个选择:
1,有话好好说,今天你东西多铺不下,我就配合你少占点地方,明天我不小心挤着你了也请多包涵。这样的好处是物尽其用,按需分配,但不便的地方是你自己决定不了,总是要看人家的心情,而且效率低啊,每次都得商量着来,万一换个同桌还得重新磨合...
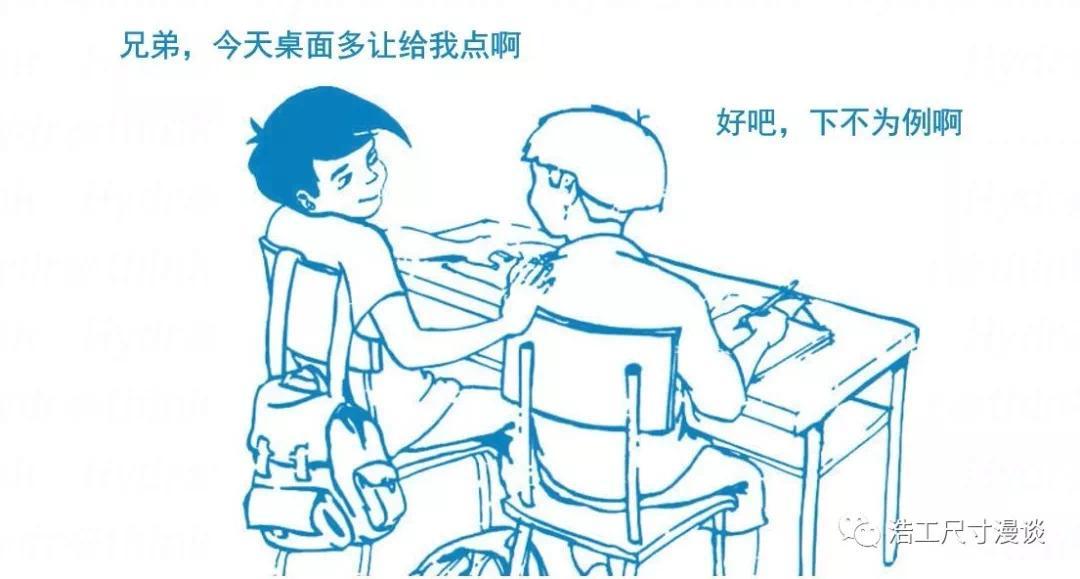
2,劳动人民的智慧是无穷的,下面这个图片说明了一切,划定一个界线,大家都不越线不就不会有干涉了,实现了自主可控,换同桌也不必再担心起冲突,完美!

映射到咱们的机械领域,上面方案1相当于配做,先做出一个零件,根据测量结果做它的配合件,对于单件试制,配合精度高的零件很OK,但是没法实现批量生产;方案2呢就是适用于流水线生产并实现互换性装配的批量制造方法了,也是咱们所要研究的对象。
但是,对于一组装配,刚才提到的那个分界线到底是什么呢?聪明的朋友们想必已经猜到了,就是咱们刚刚学过的“最大实体时效状态”的边界。
再回看下面的例子加深下理解:

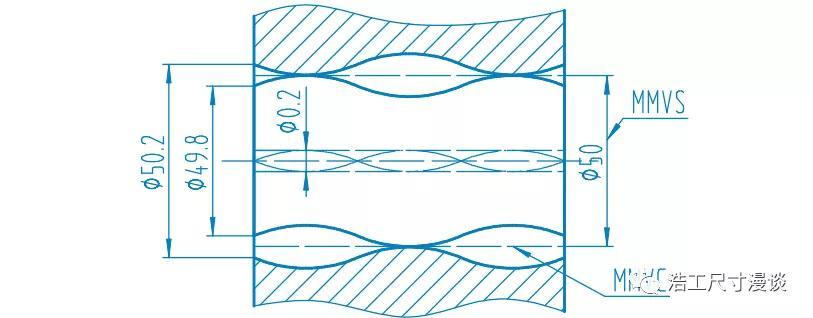
对于这个典型的孔轴配合,如果我们一开始就定义出来一个双方都要遵守的最大实体时效状态的边界,即尺寸为MMVS=Φ50的理想圆柱面,那么双方就分别被约束在了这个边界的两侧,任何材料都不会越过这个界限,这样就保证装配后的零件不会发生干涉。
以上做了这么多铺垫,现在终于要迎来咱们今天的主题之一--最大实体要求了
再回到刚才的课桌,现在已经有了一条清晰的三八线,接下来我们要考虑的问题是如何才能保证自己的书本不会越过这条线。我想了一下,必须给书本们定义一个“位置度”,来约束它可以自由移动的范围。但考虑书本有大有小,用大书的时候最危险,稍不留神就会越界,所以为了保证安全,我就以大书作为基础来定义位置度。
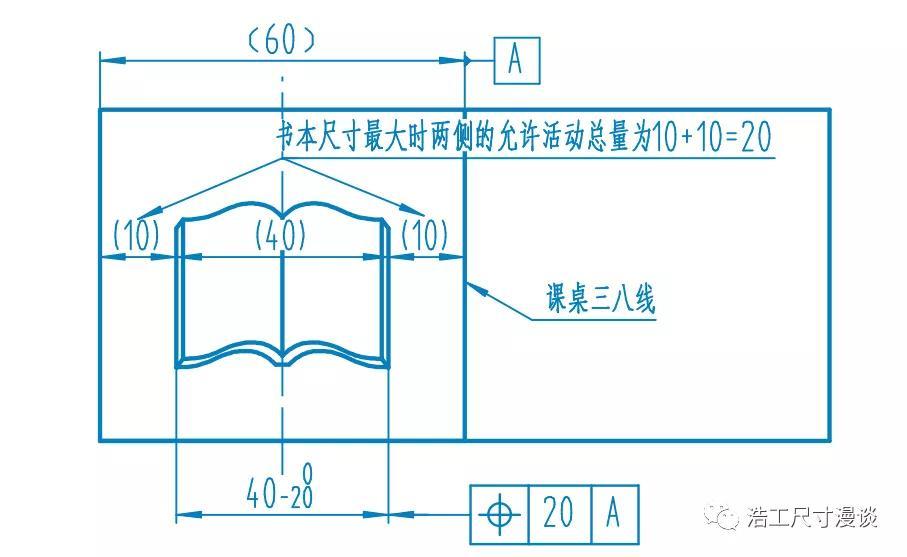
几天后我们发现一个问题,虽然这样是绝对安全的,但是我用小书的时候显得太憋屈了,明明可以多点活动空间但就是被位置度给约束了,那有没有办法让用小书的时候位置度可以自动放宽呢?这时我们就要请出“最大实体原则(M圈)”了,应用了它以后,我们标注的位置度从本质上就不是直接约束书本的位置了,而是划定了一道边界,只要书本的任何一部分都不超出这个边界即为合格。这样一来,我们又发现一个规律,就是书本的实际允许位置度跟书本的尺寸发生了关联,当书本变小时,这个变小的数值就可以补偿到它的位置度上。
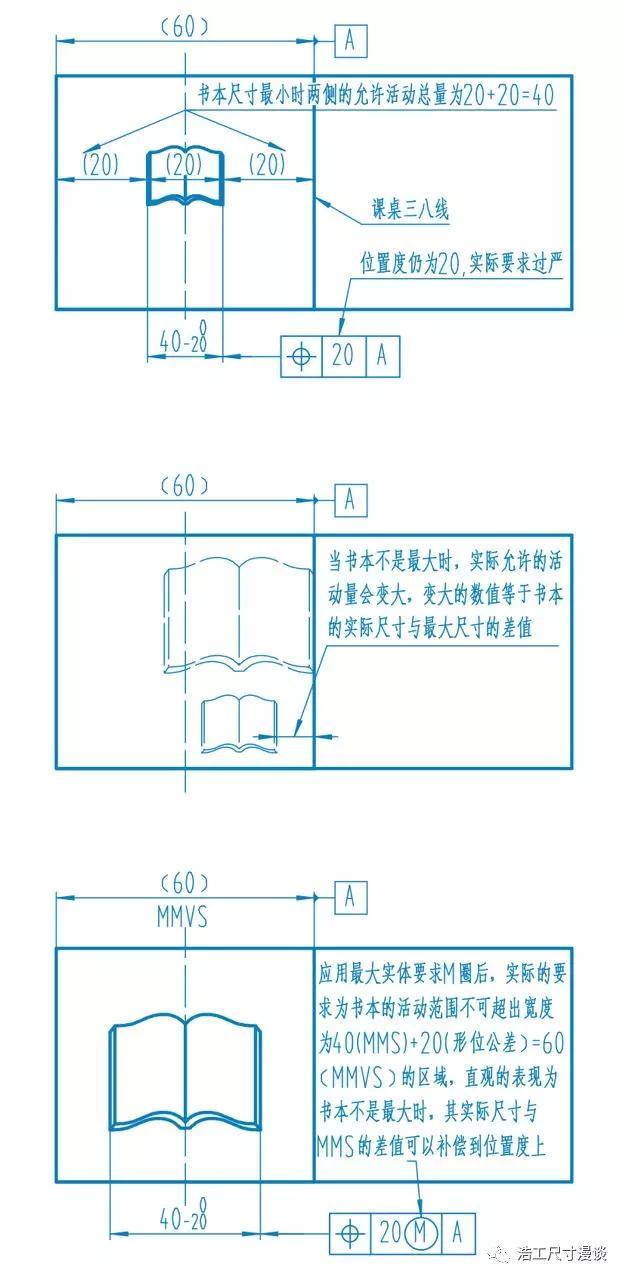
所以,应用最大实体要求时,所给定的形位公差是在最大实体状态下的适用值,当尺寸形体的实际尺寸偏离最大实体尺寸时,这个偏离的值可以补偿到形位公差上,这样在功能被满足的前提下,避免了一些零件被误判报废,太神奇了!另一点好处是,我们可以不去测量位置度,只要做一个最大实体实效尺寸的检具,能把被测对象装进去就可以判定合格了(当然前提是尺寸也要合格)。
介绍完了最大实体要求,别忘了它还有个兄弟--最小实体要求(L圈)呢,我们先照葫芦画瓢给出最小实体要求的定义:
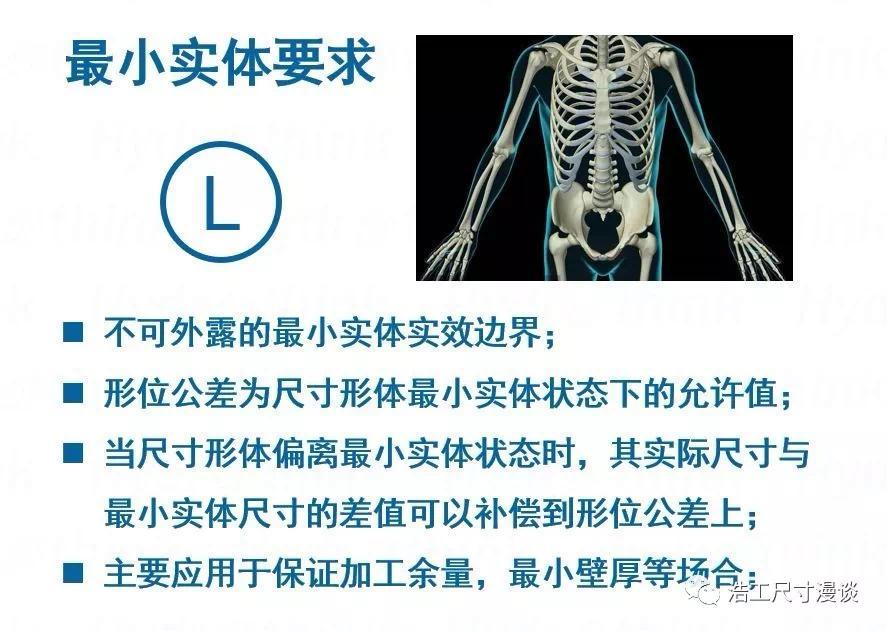
应用最小实体要求时,所给定的形位公差是在最小实体状态下的适用值,当尺寸形体的实际尺寸偏离最小实体尺寸时,这个偏离的值可以补偿到形位公差上。
前面说过最大实体要求是用来保证零件装配没有干涉的,那最小实体要求有什么特长呢?我们还是举例说明。
下面这个游戏都玩过吧,套圈。现在我们把奖品想像成平面的,套圈想象成一个圆盘,那么只要圆盘能完全盖住奖品就赢了。发现了没,圆盘最小也要和奖品直径相等,且此时允许的位置偏移为0,因为一动就把奖品露了出来,我们就失败了;但当圆盘变大时,允许的位置偏差也就相应变大了,正好符合了最小实体要求的定义。

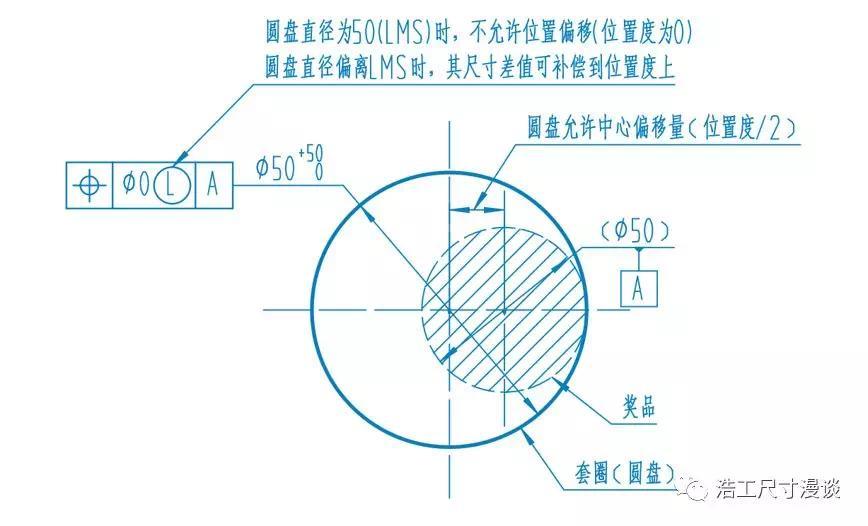
这不就是我们机械上的毛坯件和成品件的关系吗?毛坯件一定要保证能完全把成品件的几何形状包覆起来,并且还要留有最小的加工余量;还有些零件会有最小壁厚的要求,本质上和加工余量是一个道理,所以同样适用最小实体要求。如果我们从几何关系来描述,那就是最小实体实效边界永远要处在目标尺寸形体的材料内部。
OK,相关知识点还很多,但浩工的头已经很大了,所以只好先告一段落。回顾一下,在本文中我们从原理出发介绍了最大/最小实体要求的概念和功能(应用于被测要素时),要点总结如下,希望能帮大家再加深下印象:

本篇概念较多,如果一时吃不透,可以多看几遍,再结合自己实际案例或生活常识加深下理解。这里需要说明的是,以上主要是针对最大/最小实体要求应用在被测要素时的情况,其实它们也可以应用在基准上,那将又是别有一番风味。





