本文摘要(由AI生成):
本文介绍了拟合在尺寸工程中的应用,包括基准要素和被测要素的拟合。常见的拟合方法有相切法、最小二乘法和切比雪夫法。相切法适用于基准的拟合,通过理想线段或面接近实际轮廓线,反映装配需求。最小二乘法拟合追求实际轮廓上各点到拟合理想圆上对应点的距离平方和最小,通过调整圆心和圆的大小实现。切比雪夫法又称最小区域法或最小最大偏差法,通过两个同心圆柱面夹紧实际零件表面,实现最小区域和最小最大偏差的拟合。本文旨在帮助读者理解拟合的原理和应用,欢迎留言探讨共同提高。
随着大家对尺寸知识了解的深入,一个词开始频繁出现,它就是“拟合”。理解拟合是学习形位公差的必经之路,而且它偏偏还是一个需要较多数学知识才能打败的小BOSS,对脑细胞很不友好,所以我就尝试着牺牲一些自己的脑细胞来呈现一种形象化的描述,尽量把拟合的抽象概念具体化。
首先,什么是拟合,我们不去引用那些正统严谨的解释,还是举个例子。我们生活的地球上有山峰,有河谷,有高原,有盆地,看起来非常不规则,然而如果让我们描述地球是什么形状的,我想大家基本都会说“是个球样”,文艺点的会说,是个“赤道半径6378km,极半径6357km的椭球体”。这就是拟合,我们的描述已经把地球拟合成了一种规则的几何体,而忽略了细节的体现。
回到我们研究的零件,在显微镜下这些零件的表面和地球是一摸一样的,坑坑洼洼起伏不定,然而我们仍然会说,“这是一个平面”,“这是一个球面”。也就是说,我们已经在意念中完成了拟合,然而它的具体参数(比如尺寸,位置等)我们没有办法直观获得,这时就需要借助测量设备和分析软件了。
在尺寸工程中,拟合常应用在两种对象上,一种是基准要素,一种是被测要素。基准要素好理解,因为基准一定是理想的几何要素,它就是通过基准要素拟合得到的;被测要素要根据对应的标注来确定,既有可能是实际的表面要素,也有可能是拟合而成的虚拟要素。
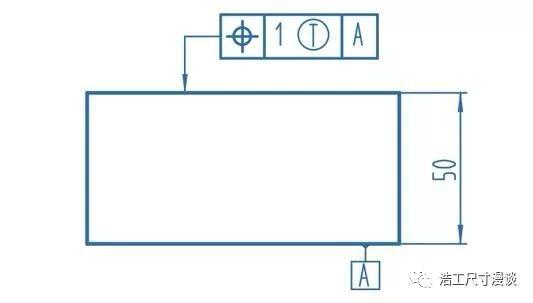

拟合的方式常见的有相切法,最小二乘法以及切比雪夫法三种,我们来一一了解下。
相切法拟合:
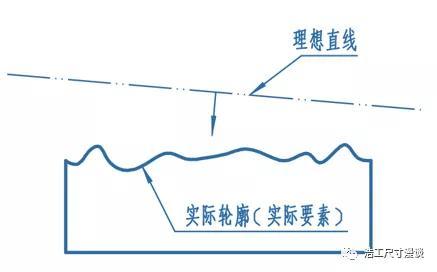
这是最常见的一种拟合方法,也是最亲民,最容易理解的方式,尤其适用于基准的拟合。既然是相切,基本上就离不开线和面了,那么相切线/面如何获得呢?我们看下图,对于一条待拟合的实际轮廓线,我们可以想像一条对应形状的理想线段去接近它,当两者稳定贴合时,该理想线段就是该轮廓线的相切法拟合线。当然相切不仅仅可以应用于直线或平面,像最小外接圆/圆柱,最大内切圆/圆柱等本质上也是由相切法拟合而得。前面文章中我们提到过,GD&T中以装配作为第一考虑,如果我们进一步思考一下会发现,相切法其实就是反映的装配需求,相切法拟合出来的形体通常就是该要素的实际作用形体。

最小二乘法拟合:
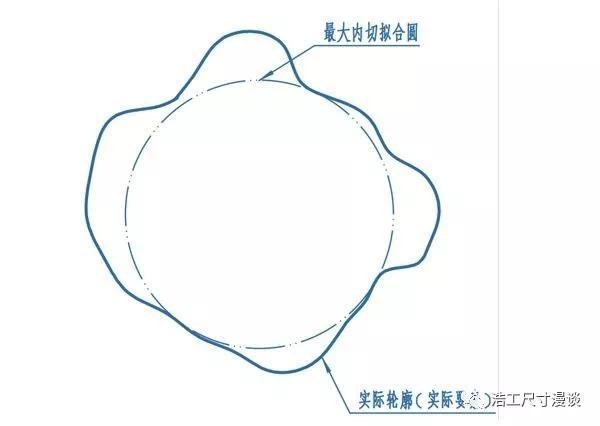
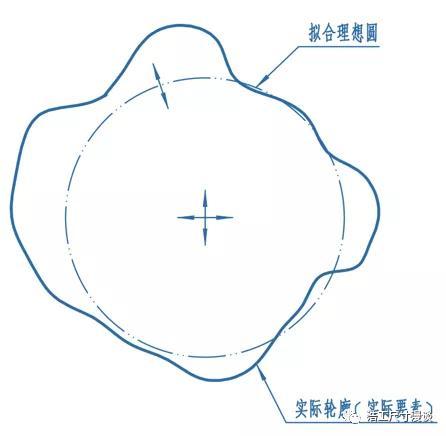
这是ISO GPS中比较偏爱的一种拟合方法,比如孔的位置度,被测要素就是该孔的中心线,即各截面最小二乘法拟合圆的圆心连线。那我们就以一个圆截面为例来看它的最小二乘法拟合圆究竟如何获得。首先,最小二乘法拟合完成的状态是实际轮廓上各点到拟合理想圆上对应点的距离(拟合误差)平方和最小,直观来说,就是下图中各线段长度的平方和最小。
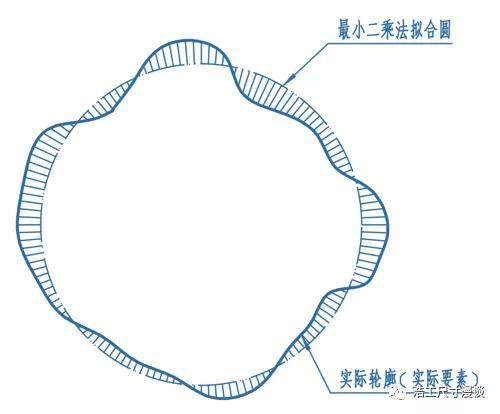
这里事实上有两个变量,一是圆心的位置,二是圆的大小,所以拟合的过程就是反复调整这两个变量,找到一个使误差平方和最小的组合。我们这里不来具体谈这两个参数是怎么算出来的,因为现在的科技基本保证大家无需手算,明白原理就好。
切比雪夫法拟合:
这是一个出现频率很高,让人听了就头大的名字,很多形状公差(比如平面度,圆柱度等)的公差值都是默认用切比雪夫法拟合计算的。它的另外一个名字叫Minimax法,我通常直译为最小最大偏差法,一些资料称它为“最小区域法”也是很贴切的。我们以一个圆柱面为例来直观理解下切比雪夫法是如何操作的。
如下图所示,我们有一个实际的圆柱零件,现在在它的表面内外两侧分别插入一个理想的圆柱面,两个圆柱面保持同心并向彼此靠近,我们可以想象最终的状态是实际零件表面被牢牢夹紧在两个理想柱面之间,没有任何的径向活动空间。这时我们如果再在两个理想柱面之间再插入一个中间面,此中间面就是该零件表面的切比雪夫法拟合面,而另外两个理想圆柱面则分别是切比雪夫法拟合体外边界和切比雪夫法拟合体内边界。
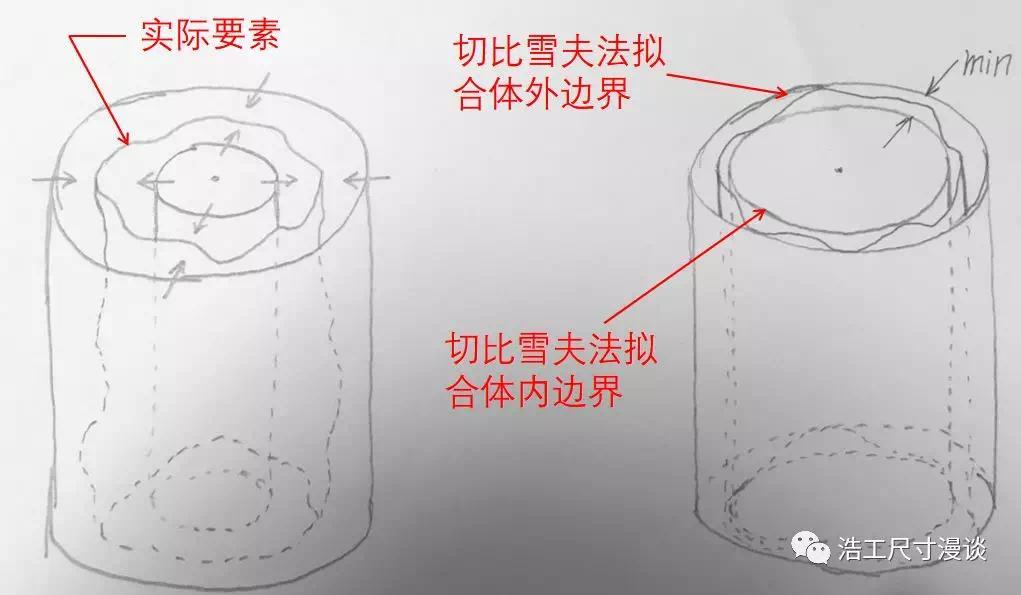
我们再来仔细看下拟合完成的状态,首先内外圆柱面的间距一定是最小的,这也解释了为什么切比雪夫法又叫最小区域法。另一方面,零件表面与切比雪夫拟合面偏差(距离)最大的点分布在拟合面的两侧,且这个偏差是所有拟合状态中最小的,所以切比雪夫法也称为最小最大偏差法。
为了加深理解,我们来考虑一个问题,对于刚才的零件表面,如果我们先找到它的最小外接圆柱,然后从内部做同心圆柱往外撑,当这个内部的圆与实际轮廓表面接触时,是不是就完成了切比雪夫法拟合呢?要回答这个问题,我们只要思考一下此时两个同心圆柱面的距离是不是最小的,咱们一起来分析下。
假设我们的圆柱做成了下面上图的样子,相当于一个正圆被切掉一块,这时它的最小外接圆会和它的弧形轮廓重叠,现在我们从内部做一个同心圆与被切部分相接,就是我们刚才提到的状态。看起来好像此时两个圆的距离最小,但实际上如果此时外接圆变大,这个距离是会继续缩小的,直到下面第二图的状态,所以第二图才是切比雪夫法拟合的完成状态。
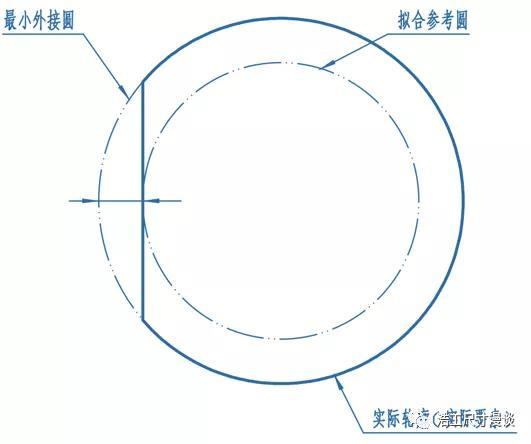
好了,以上主要介绍了三种常用的拟合方法及其原理,能力有限,讲的可能不太严谨,但仍希望对大家有所帮助。同样欢迎留言探讨,共同提高。