频域自适应滤波理论分析获进展
来源:中国科学院声学研究所,作者:中科院噪声与振动重点实验室 杨飞然。
自适应滤波是信号处理学科的一个重要分支,它在声频工程、通信和雷达等很多领域获得广泛的应用。在声学系统辨识和建模(如主动噪声控制、回声抵消、啸叫抑制和房间均衡等)应用中,频域自适应滤波算法因具有较低的复杂度和较好的收敛性能已成为标准解决方案。在过去的四十年里,科研人员针对频域自适应算法做了很多理论分析工作。但是,已有的理论分析大多针对特定类型输入信号且采用了大量的强假设,并缺乏对一些基本问题的回答。
近年来,中国科学院声学研究所的杨飞然、杨军研究员与德国波鸿鲁尔大学通信声学研究所的科研人员合作,提出了一种通用的统计分析方法,实现了对一大类频域自适应滤波算法的精确理论分析。该理论模型解决了一些长期悬而未决的问题,纠正了现有的一些错误观点,加深了科研人员对这一类自适应算法收敛行为的理解。
在这项研究中,科研人员们对频域自适应算法和分块频域自适应算法的收敛性能进行了分析,具体如下。
频域自适应滤波算法收敛性能分析:科研人员用一种新统计分析方法,提供了四种不同版本频域自适应算法的瞬态和稳态收敛性能闭式解,并得到了保证算法稳定的步长上界。该研究适用于具有任意概率密度函数的输入信号,克服了已有研究只对高斯或白噪声信号有效的缺陷;该研究在稳定性步长范围内获得了目前最为准确的理论解,克服了过去分析只对小步长有效的局限。该研究成果2019年1月在线发表于 IEEE Transactions on Signal Processing 。
欠定频域自适应滤波算法收敛性能分析:当自适应滤波器阶数小于实际系统的阶数时,无约束的频域算法收敛到无约束的维纳解,而约束的版本则不能,这使得无约束算法比约束算法具有更低的最小MSE (Mean-Square Error)。科研人员也证实均值最优并不一定带来MSE最优,这纠正了先前一些研究成果中的错误结论,并强调了MSD (Mean-Square Deviation) 和MSE两个技术指标不一定正相关。该研究成果先后2019年6月和10月在线发表于 IEEE Transactions on Circuits and Systems I: Regular Papers 和 Signal Processing 。
分块频域自适应滤波算法收敛性能分析:该研究在充分建模场景下建立了一类分块频域自适应算法的严格理论模型。研究表明约束分块频域自适应算法可以在均值意义上收敛到真实的系统脉冲响应,无约束的版本则总是收敛到有偏解,研究人员给出了该解的表达式,并指出约束和无约束的分块频域算法都可以收敛到维纳解。该结论事实上否定了经典专著 (S. Haykin的 Adaptive Filter Theory 和A. Sayed的 Fundamentals of Adaptive Filtering) 认为无约束频域算法不能收敛到维纳解的观点。该研究成果2021年8月在线发表于 IEEE Transactions on Signal Processing 。
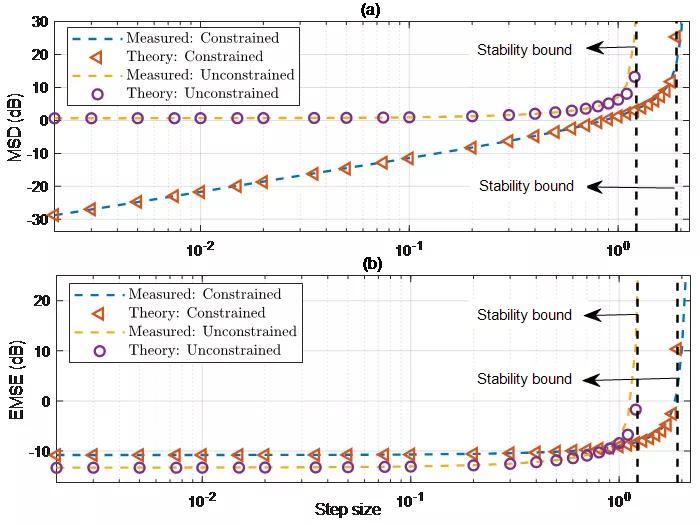
图1 步长归一化的标准频域自适应算法在欠定建模时的稳态MSD和EMSE(Excess Mean-Square Error)。均匀分布的自回归(Autoregressive,AR)过程作为输入。约束的频域算法总是比无约束的版本具有更低的MSD。当步长小于某个值时,无约束频域算法具有更低的EMSE;但当步长大于该值时,约束版本则具有更低的EMSE(图/中科院声学所)
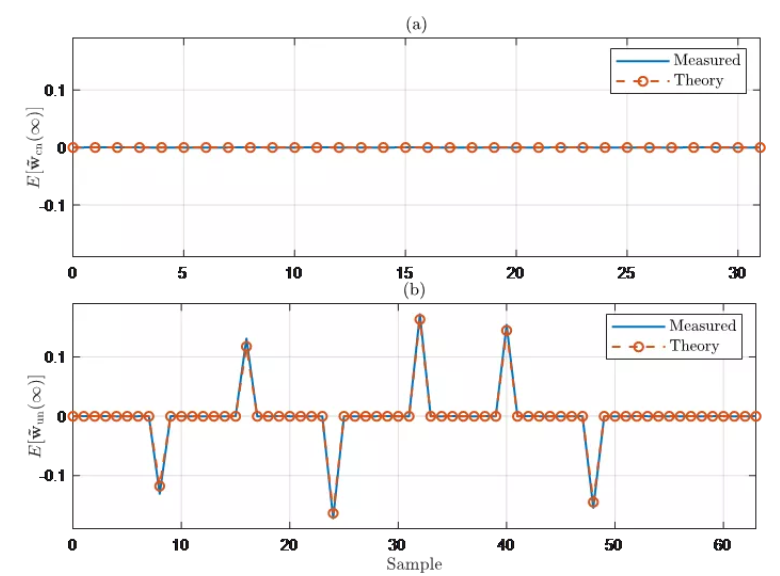
图2 步长归一化的分块频域自适应算法的稳态均值权系数。均匀分布的AR过程作为输入。上图表明约束的分块频域自适应算法能均值收敛到真实的系统脉冲响应;下图表明无约束的版本则收敛到有偏解(图/中科院声学所)
该系列研究得到了中国科学院青年创新促进会和中国科学院声学研究所青年英才计划等项目支持。
参考文献:
[1] F. Yang, G. Enzner, and J. Yang, “A unified approach to the statistical convergence an alysis of frequency-domain adaptive filters,” IEEE Trans. Signal Process., vol. 67, no. 7, pp. 1785–1796, Apr. 2019.
[2] F. Yang and J. Yang, “Convergence an alysis of deficient-length frequency-domain adaptive filters,” IEEE Trans. Circuits Syst. I, vol. 66, no. 11, pp. 4242–4255, Nov. 2019.
[3] F. Yang and J. Yang, “Mean-square performance of the modified frequency-domain block LMS algorithm,” Signal Process., vol. 163, pp 18–25, Oct. 2019.
[4] F. Yang, G. Enzner, and J. Yang, “On the convergence behavior of partitioned-block frequency-domain adaptive filters,” IEEE Trans. Signal Process., vol. 69, 2021.





