惯性和摩擦对一个失重试验的影响
来源:尤明庆科学网博客,作者:尤明庆 河南理工大学教授。
网上的一个演示实验“3 1=3”:细线绕过轴承,两侧分别悬挂1个和3个砝码;其无摩擦运动时轴承的受力正好是3个砝码的重量。
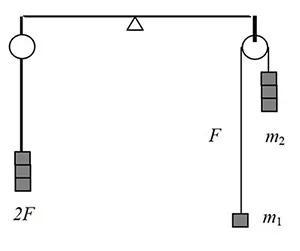
依据牛顿第二定律,砝码的运动满足
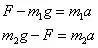
消去加速度a,有
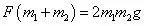
即
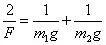
绳中拉力F 是两侧运动砝码重量的调和平均,若m2=3m1,则F=1.5m1g,2F=3m1g。
博友张云老师说“天平应该只能平衡很短的时间,这种昙花一现般的实验现象真是让人惊艳”。我说“看的只有视频没有具体说明。时间很短,说是0.2秒。时间过短是这个实验的一个欠缺,因为天平臂有惯性,短期的水平并不意味着真正的平衡。我主要想说的是,现在我们多用算术平均来评价系统的总体特性,例如居民平均收入,有时候这样的平均值不是调和的”。
试验是建立和检验自然科学(如物理知识)的重要手段。费恩曼认为“数学不是科学,因判断其对错不需要试验”,当然“if a thing is not a science, it is not necessarily bad. For example, love is not a science”。不过,现今中文语境下的“科学”已经不完全等同于英文的 science。
可靠的试验能够准确反映系统参数之间的关系,测试数据具有分析或判断所需要的精度。不过,试验系统中影响因素较多,对试验结果的可靠性需要具体分析。
“3 1=3”试验中加速度约为0.5g,因而砝码在0.3秒时间的运动距离约为22cm,这实在有些短。如果将天平斜放到桌角使其臂端伸出桌面,将砝码可运动的距离增加到1米以上就好了。不过,若真是这样,天平或许就不再能平衡,这个失重的演示试验就不能成立啦。需要知道,轴承旋转部分具有质量,对运动以及细线受力也会产生影响。
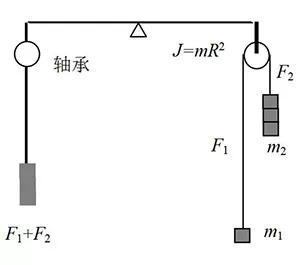
假设轴承外径为R,转动惯量J=mR²,那么
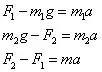
得到加速度
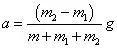
以及
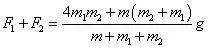
m=0就是前述2F,考虑轴承转动天平受力增大
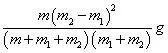
若m2=3m1 而m=0.2m1,天平右端的实际受力将达到3.05m1g,对天平而言并不能忽略。只是天平臂的转动惯量较大,其依稀可见的向右缓慢倾斜被快速下降的砝码所掩盖。
使用固定的圆柱支承细线可以消除上述惯性的影响,但圆柱摩擦可能使试验完全失去可靠性。绕过圆柱半周的细线两侧作用力满足F2=kF1。k≤m2 /m1 时,
砝码运动的加速度为
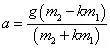
支承细线圆柱受力为
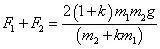
在阻力系数k=2.5时,上式为3.82m1g,天平更不能平衡。
塑料绳绕过不锈钢茶杯,两侧茶杯数为2和5时正好进入临界状态:可保持静止而稍作扰动则滑动。如果绕过圆柱一周半,因2.5*2.5*2.5=15.625,两侧重量的比值达到15也可保持静止啊。

圆柱的摩擦使绳子中张力增大,而张力又引起绳子对圆柱的压力增加,即摩擦力的增大,正反馈引起指数形式的增加。
指数规律与“利滚利”:
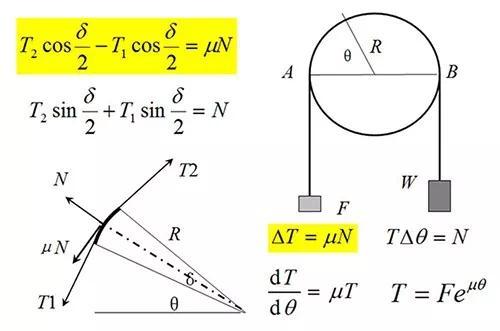
照片中塑料绳绕过不锈钢茶杯半周的阻力系数k 为2.5,相应的静摩擦因子μ 略大于0.29;若是细麻绳与木杆,静摩擦因子或许有0.8,则绕圆柱时半周阻力系数为12.3,而一周半则可达到1880以上呢。





