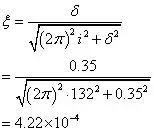衰减法阻尼测试

来源：声振测试，作者：于长帅。

阻尼减振技术是一门与机械、材料、力学等多学科相关的技术，利用能量耗散的机制对设备起到减振降噪的作用。为设计良好的附加阻尼结构，需准确地获得材料的阻尼性能，实际中常用试验的方法获取材料的阻尼性能。悬臂梁法是常用的一种阻尼测试方法，具有附加阻尼小的优点。

悬臂梁法是一种专门针对梁试件的阻尼测试方法，通过测试梁的共振频率，可以计算出材料的杨氏模量，试件的阻尼比可以通过半功率带宽法和衰减法获得，下图为悬臂梁法典型试件的示意图。

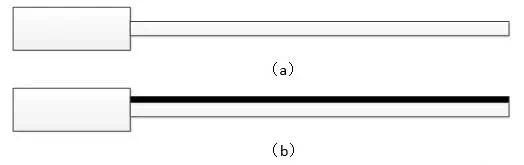
(a) 单层梁试件；(b) 复合梁试件

图1 悬臂梁法典型试件的示意图

本文对单层梁运用衰减法识别第一阶模态阻尼比进行试验测试研究，后续将进行较深入的讨论。

衰减法理论推导

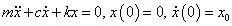
也可以写成：

其中系统的固有频率为：

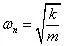
系统阻尼比为：

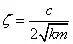
求解上式得：

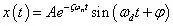
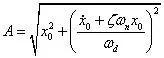
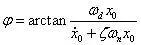
式中，A 为振动幅值，φ 为初相位，ωd 为有阻尼固有频率，ωd =√1-ζ²ωn。

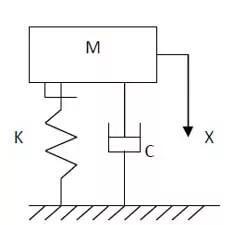
图2 单自由度系统模型

上式的图形如图3所示。

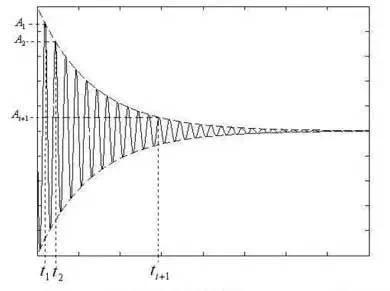
图3 自由衰减曲线

此波形有如下特点，振动周期：

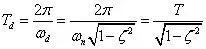
固有频率：

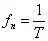
振幅按几何级数衰减，减幅系数：

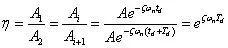
对数减幅系数：

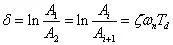
对数减幅系数也可以用相隔i个周期的两个振幅之比来计算。

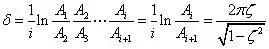
从而可得：

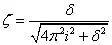
阻尼测试

阻尼测试系统框图如图4所示，力锤单次冲击试件，试件做自由衰减振动，非接触传感器拾取振动的位移信号，送入数据采集分析系统进行保存和分析。对于该测试，力锤敲击应当短促以确保宽带激励，但敲击力不宜过大，以避免试件产生非线性振动；试件夹具应当具有足够大的刚度，夹持力应当足够大，保证试件与夹具间不产生摩擦，避免引入额外的误差。

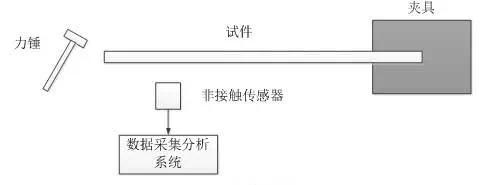
图4 阻尼测试系统框图

对于某悬臂梁，现场测试照片如图5所示。

图5 悬臂梁阻尼测试

悬臂梁的自由衰减位移响应曲线如图6所示，从图中可以看出，位移的时域响应是板结构多个频率的叠加结果，本测试关注板结构第一阶模态频率和阻尼，因此需要对下图的时域数据进行低通滤波处理。

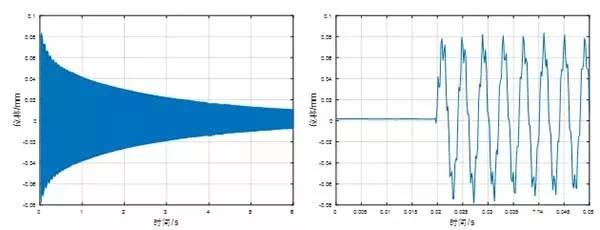
图6 自由瞬间位移响应曲线

巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数。巴特沃斯滤波器是根据幅频特性在通频带内具有最平坦特性定义的滤波器。巴特沃思滤波器的低通模平方函数表示：

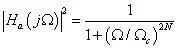
式中，Ωc 为截止频率，N 为滤波器的阶数，下面归纳了巴特沃斯滤波器的主要特征：

• 对所有的N，

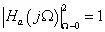
• 对所有的N，

  
  

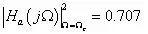
       即

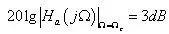
• |Ha(jΩ)|²是Ω的单调下降函数。

• |Ha(jΩ)|²随着阶次N 的增大而更接近于理想低通滤波器。

如下图7所示，可以看出滤波器的幅频特性随着滤波器阶次N 的增加而变得越来越好，在截止频率Ωc 处的函数值始终为1/2的情况下，通带内有更多的频带区的值接近于1；在阻带内更迅速的趋近于零。

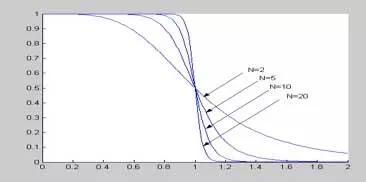
图7 巴特沃斯低通滤波平方幅频特性函数

对图6中的信号进行巴特沃斯滤波，滤波后的曲线如下图所示。

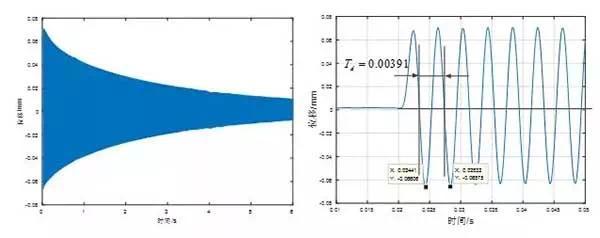
图8 自由衰减位移响应滤波后曲线

从上图8可以识别出一阶振动周期0.000391s，由于振动周期太小，选曲线两个点 (0.03438，0.0708) 和 (0.5506，0.04988) 进行一阶模态阻尼比的计算，两个点相隔的振动周期为132个振动周期。

图9 自由衰减位移响应滤波后曲线（阻尼比计算选择点）

对数减幅

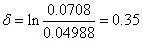
根据

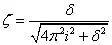
得