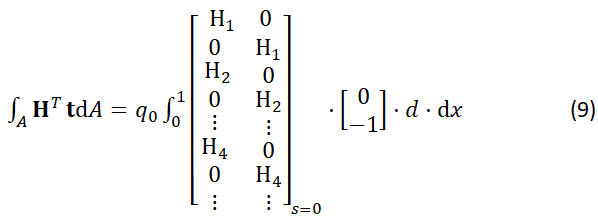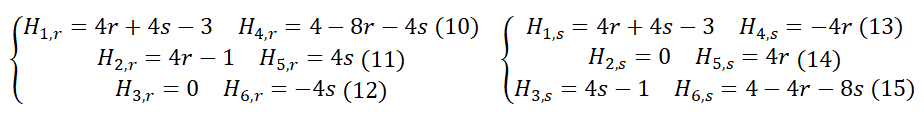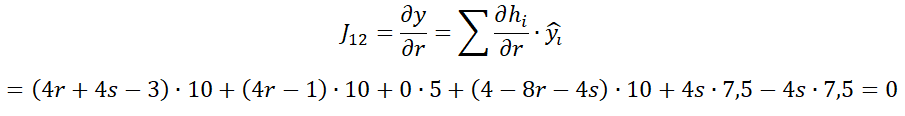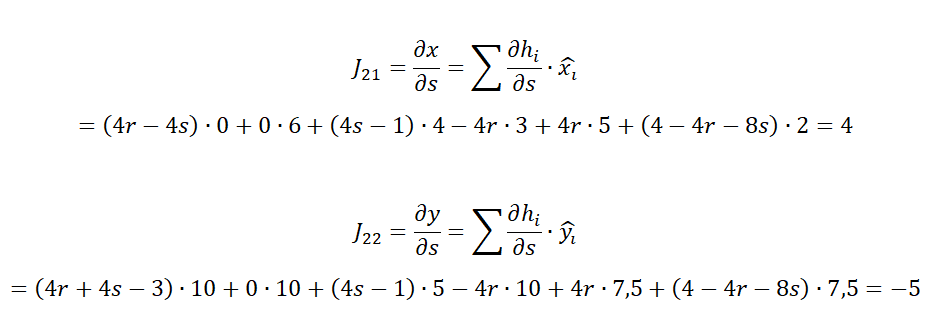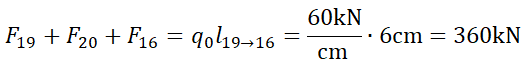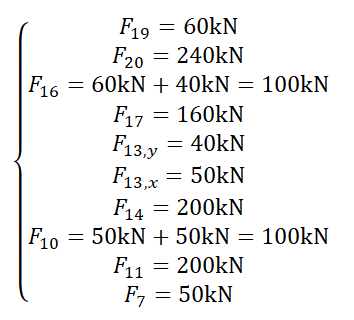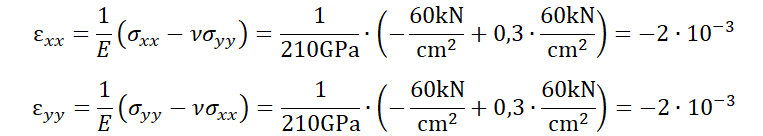我的德国汉诺威大学土木工程有限元学习史
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐/内容稀缺
汉诺威大学 university of hannover导读:受仿真秀平台邀请,我于9月2日分享了一堂线上公开课《有限元分析在岩土工程中的应用概述》,目前在仿真秀官网和App支持回看。其中,我以自己不多的储备与国外求学经历分享了我对这一话题的一些浅薄的看法。荀子曰:“青,取之于蓝,而青于蓝;冰,水为之,而寒于水。”又云:“君子生非异也,善假于物也。”若为诸君所假,吾将不胜欣喜。回想起来,学习有限元的经历几乎伴随着我在德国求学的整个过程。
汉诺威大学土木工程专业的硕士课程里的五门必修课,其中两门课与有限元相关, 固体力学、有限元方法在静力学与动力学中的应用(Finite Elemente Anwendungen in der Statik und Dynamik,以下简称FEA)。再加上我被要求在两学期内补修两门本科课程:弹性力学 (Elastomechanik)与数值力学(Numerische Mechanik)。于是,对我而言的必修课中有限元七占其四。弹性力学为有限元打基础,数值力学讲授线弹性有限元,固体力学(Festkörpermechanik)与FEA这两门课则讲授非线性有限元。所以我和我的同学都戏称,汉诺威大学应该改称汉诺威有限元大学。

N教授与M老师是我有限元方面的启蒙老师。毫不夸张地说,是M老师把我领入有限元的大门,耐心地听我用蹩脚的德语提问,一点一点地讲解。从线弹性有限元的Patch-Test, Jacobi Matrix到塑性力学的 Newton-Raphson, Return Mapping。在另一门有限元的必修课FEA中,对几乎所有的非线性有限元内容进行了全方位讲授,其中重点讲授几何非线性。犹记得每周四下午15:45 在R教授深入浅出的讲授下,我学到了由欧拉杆压杆稳定问题引申出的Verzweigungsproblem (engl. Bifurcation Problem),由Von Mises 桁架引申出的Durchschlagsproblem (engl. Snap-through Problem) 等等。
汉诺威大学读书馆
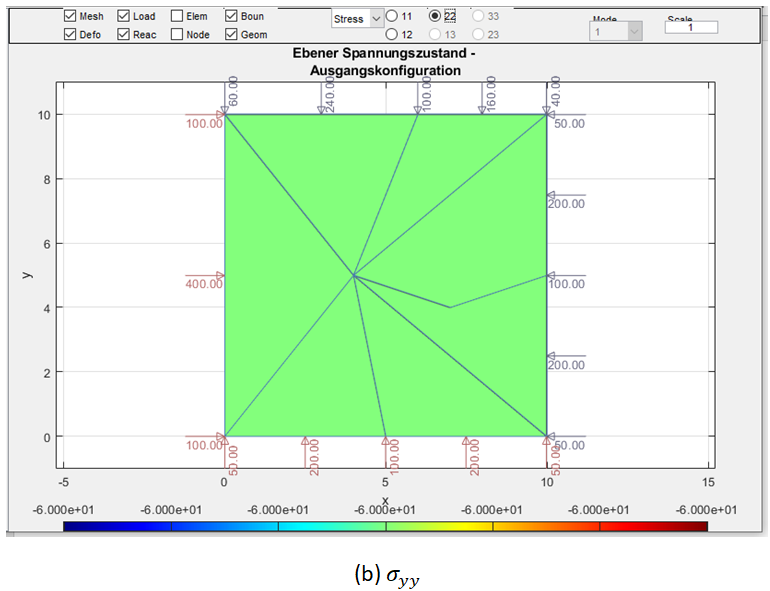
有限元法的实质,是一个基于能量法(如Ritz 方法&Galerkin 方法)配合弱形式基于各种实际情况假设近似求解平衡偏微分方程的工具。口试时被N教授问到的有关有限元的第一个问题是:有限元方法的优点是什么?当时我回答:通过网格的精细划分可以极其精确地模拟几何形状。N教授当时宽容地笑笑,换了更简单的问题继续提问。后来逐渐明白,N教授想听到的答案是“有限元使用了弱形式弱化了平衡方程,使得平衡条件只需要在积分意义上满足,从而可以选择次数更低的形函数求解偏微分方程,同时所有的力亦均可以等效节点力替代,大大降低了求解难度”。下面以有限元经典案例Patch Test为例,拿出有限元里的一小部分内容来示例,即如何计算等效节点力。式中左侧 表示内力虚功,右侧则分别为体力虚功及面力虚功。Patch-Test是在一个平面应力状态的正方形板(边长为l,板厚为d),同时在右侧两个面加均布荷载q0,左侧则分别施以滑动支座,如图1所示。
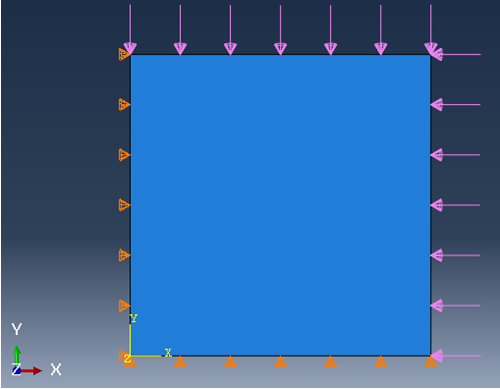
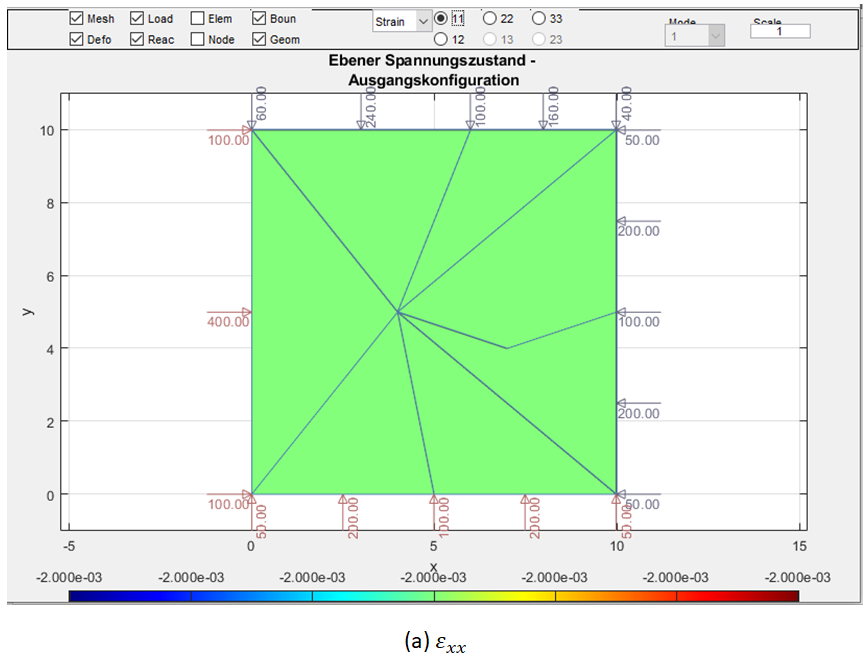
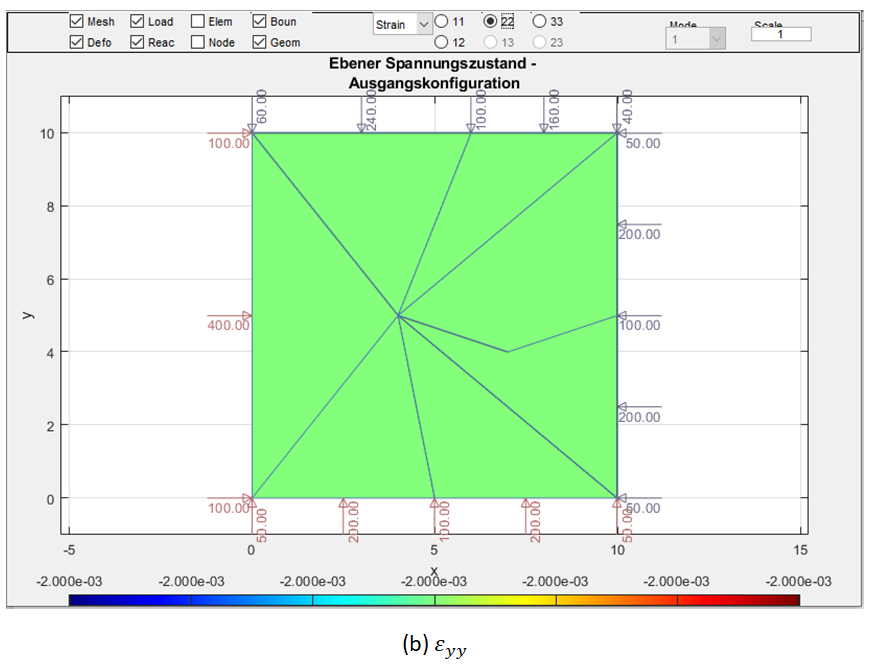
若以解析解求解易知,此时的应力为 。应变为 , 。同时,Patch Test亦可如图2所示建立有限元网格,该网格以二次形函数的三角形单元进行网格划分。在本例中,边长 =10cm,板厚 =1cm。均布荷载 =60kN/cm,所用材料为钢,其杨氏模量 =210GPa, 泊松比 =0.3。

式中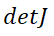 为雅可比矩阵的值。
为雅可比矩阵的值。

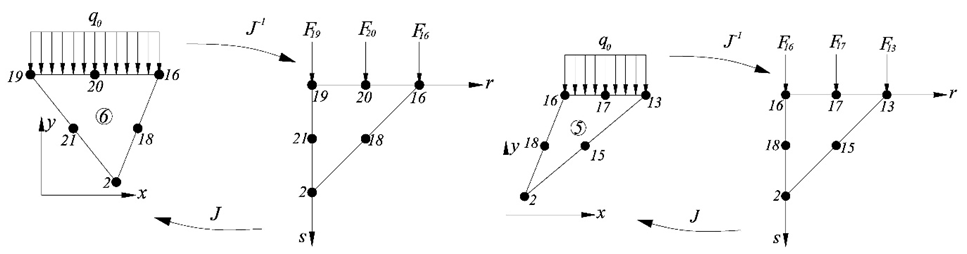
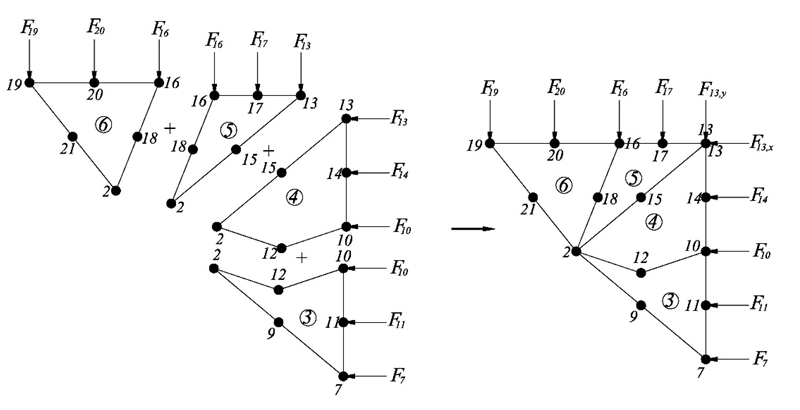
计算等效节点力的前,需用雅可比矩阵对单元进行投影,使之适用于单元的自身局部坐标(参见图3,图4&图5)。
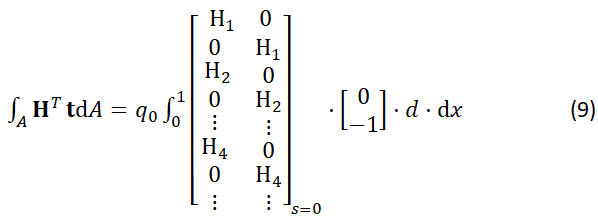
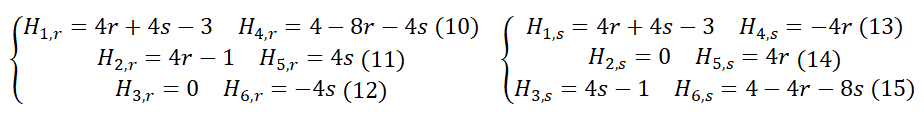
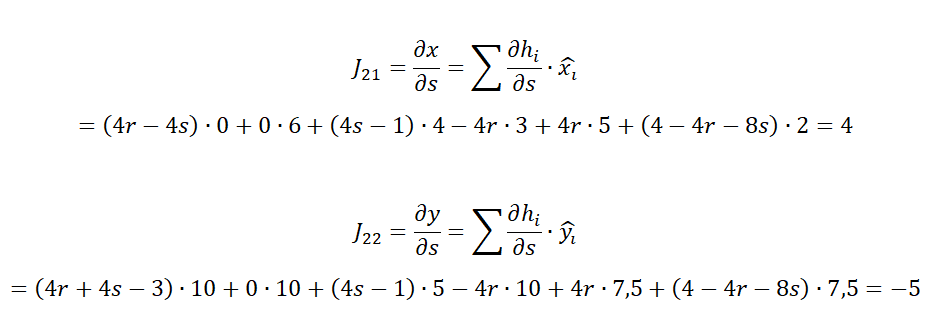

相同过程对3号、4号及5号单元如法炮制(如图4&图5),并组装(Assembly,如图6)得到 kN/cm2(如图8),与解析解 = kN/cm2相符。
总之,在本例中,使用有限元的弱形式计算得到的等效节点力取得了与解析解同样的效果,证明了弱形式在本例中的正确性。三、土木工程有限元分析入门
为了增进与土木工程有限元分析研究人员和理工科学子进一步交流,9月9日19时《超级话题》第十三期,我与老中铁设计孙智道老师将在仿真秀土木工程行业群,畅聊《土木工程有限元分析入门》学习历程、学习方法、学习资料和学习案例等。以下是课程安排,诚邀理工科学子和土木工程有限元分析研发人员进群沟通交流,并为200名用户提供直播回看和资料下载。
本期主题
土木工程有限元分析入门
《如何成为年薪30-50万的土木工程师》
本期嘉宾
曹舒瀚,现为汉诺威大学(Leibniz Universität Hannover) 岩土工程研究所 (Institut für Geotechnik) 研究员,在读博士。主要研究方向为浅基础在循环荷载作用下循环变形的数值模拟。授课内容包括土动力学、地下特种结构与填埋场技术、岩土工程数值模拟等研究生课程。

孙智道 仿真秀专栏作者
孙智道,现就职于中铁工程设计咨询集团有限公司,主要从事铁路桥梁设计及涉铁安全评估工作。累计完成近五十项安全评估工作,包括隧道、桥梁、基坑、框架、顶管、路基等下穿铁路安全评估,以及软土路基计算等项目。于集团内开展安全评估培训课程,并两次通过直播开展PLAXIS在涉铁安评的应用讲座。
分享主题
曹舒瀚 汉诺威大学岩土工程研究所研究员
1、我的土木工程有限元学习成长史
2、土木工程有限元分析理论学什么
3、土木工程有限元分析工程应用难吗
孙智道 中铁工程设计咨询集团工程师
1、土木工程有限元行业流程与方法
2、土木工程有限元分析案例实操
活动时间
2021年9月9日(周四晚19:00)
活动形式
活动专属行业群分享(图文\语音)
如何报名
长按二维码
可申请加入土木行业交流群【限200人】

对于本次活动有任何疑问
即日起,仿真秀平台将开启土木工程有限元分析交流月,将给理工科学子和研发工程师带来多场精彩直播和社群讨论,在文章末尾附件下载仿真秀土木行业仿真学习包(持续永久更新),如果遇到问题,请在文章下方留言,或者联系平台小助手人工领取。
声明:原创作品,首发仿真秀App,部分图片和内容源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。喜欢作者,请点赞和在看 
获赞 10106粉丝 21586文章 3547课程 219



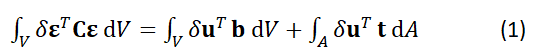




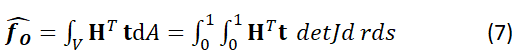
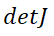 为雅可比矩阵的值。
为雅可比矩阵的值。