关于自由模态和约束模态分析的几点常识

概述

在汽车结构有限元分析中，模态分析是最简单的分析项。我们通常所进行的模态分析都是实模态分析，计算中不考虑阻尼，计算结果提供了无阻尼的固有频率和振型。

模态分析得到的模态参数可用来预测结构与路面激励或其它系统发生相互作用的可能性，通过结构的合理设计来避免共振。

模态分析的结果也可用来将系统振动方程中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标描述的独立方程，从而实现模态叠加法求结构响应，进而可以确定动刚度、频响函数、动强度以及疲劳寿命。

此外，利用模态分析所提供的各阶模态参数,联合结构响应求得外激励，从而实现载荷识别。

关于自由模态分析

所谓自由模态分析，指的是对处于自由边界的结构进行模态分析，此时结构未受到任何位移约束。自由模态分析可能会得到固有频率为0的模态，称为刚体模态。一般情况下，特征值计算得到的前六阶模态为刚体模态。除了刚体模态，其它各阶模态称作弹性模态。

刚体模态和弹性模态的区别

弹性自由模态的固有频率必然大于0。而刚体模态的固有频率理论上应该为0，计算误差会导致刚体模态的固有频率结果不绝对为0，而是非常接近于0的数值。

弹性自由模态是一种弹性变形状态，描述的是结构上各位置之间的相对变形，其应力分布不为0（通常叫做模态应力）。而刚体模态描述的是结构刚体移动（通常是绕质心的平动和绕质心的转动；当采用不同的坐标系时，也不一定绕质心平动或转动），不存在弹性变形，所以其应力分布处处为0。

既然刚体模态不产生应力，我们在用模态叠加法求结构动应力时，可以忽略掉各阶刚体模态，仅对弹性模态进行模态分解、求模态坐标响应和叠加模态应力等操作。

弹性自由模态是质心位移为0的变形状态

弹性自由模态描述的是结构以某种弹性变形模式做自由简谐振动，在振动过程中结构变形程度是按正弦曲线不断变化的，但变形后的质心位置始终保持不变。也就是说，对于任何一阶弹性自由模态振型，虽然弹性变形导致了不为0的位移场分布，但结构质心的位移一定为0。

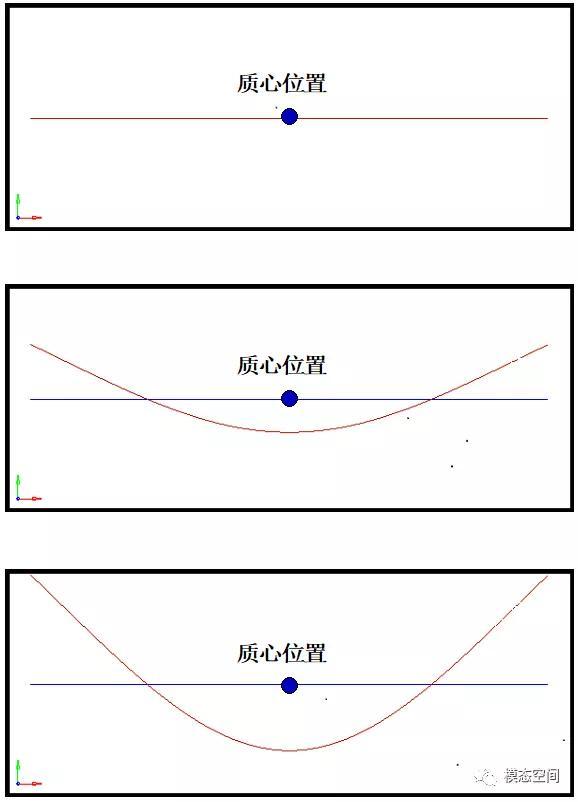
图1 弹性自由模态的结构质心保持静止

以上结论可用公式推导来证明，也可从物理上简单论证。结构按某阶弹性自由模态做自由简谐振动时，结构上所有的点同时达到最大振幅，此时刻各点的速度为0，即此时刻结构的总动量为0。结构在做自由简谐振动时，未受任何外力作用，振动过程中结构的总动量必然保持恒定。所以振动过程中结构的总动量始终为0，这意味着结构质心的速度为0，即结构质心始终保持静止。

弹性自由模态中存在模态节点

对于任一阶弹性自由模态，我们指定任意一个方向，则质心在该方向的位移一定为0。这就要求结构某一部分在该方向的位移为正，而另一部分在该方向的位移为负，考虑到位移场的连续性，必然有某些点在该方向的位移为0。

在弹性模态中，位移为0的点称为模态节点，如图2所示。

图2 模态节点示例

有一点需要注意，对于某阶弹性自由模态，针对任意一个方向，我们都可以找到在该方向位移为0的点，但是我们不一定能找到XYZ向位移同时为0的点。所以我们在讨论模态节点时，严格说来应该预先指定位移方向（主要关注方向），因为所有方向的位移都为0的模态节点未必存在。

关于约束模态分析

如果我们对结构的某些自由度施加约束（通常是0位移约束），针对这种约束状态计算得到的模态就叫做约束模态。

约束模态中也可能出现刚体模态

如果我们对结构施加的约束并不足以完全限制结构的刚体的位移，则约束模态的前几阶仍然是刚体模态。例如我们约束某个三维结构中某点的X向自由度，然后做约束模态分析，则前五阶模态均为刚体模态，描述了结构在除X向之外的其他五个方向上的刚体移动。大多数情况下，我们施加的约束都足以限制结构在各个方向的刚体的位移，此时所有的约束模态都是弹性模态。

约束模态可等效为无约束状态下的受迫振动

弹性约束模态是受约束结构的固有振动特性。在约束点位置，约束实质是以约束反力的形式作用于结构，约束反力阻碍该点的运动，使该点受约束自由度的位移为0。因此，我们可以将弹性约束模态等效为在无约束状态下的受迫振动，即结构去掉约束，处于完全自由状态，在原约束位置处施加力或力矩（约束反力）激励，激励的频率、大小和相位经过仔细调整，恰好能保证原受约束自由度的位移为0。

弹性自由模态可视为约束模态

前面提到过，弹性自由模态中存在位移始终为0的自由度，我们如果对这些点的0位移自由度中的一个或者多个施加约束，并不会产生约束反力，对结构的自由间隙振动无任何干扰。此时的约束模态跟原自由模态是在振型和频率上都是一致的。前提条件是针对某一阶模态，因为不同阶的模态节点位置会发生变化。

所以弹性自由模态可以看做是一种特定的约束模态，位移约束恰好施加在其0位移自由度上。

受约束结构必须用约束模态分析吗?

在实际工程应用中，像飞行中的飞机、太空中的卫星这种完全自由状态的结构是很少见的，大部分情况下结构都是受到各种约束。有人考虑到约束模态跟自由模态无论是在振型上还是固有频率上都存在非常大的差别，所以他们应按实际情况施加约束条件，进行约束模态分析。

但实际操作时，施加符合实际的约束极其困难。有些约束非常复杂，且包含有非线性因素，很难简化为可用于线性有限元分析的边界条件。而且大部分约束不是完全刚性的，用简单的0位移边界条件来模拟实际上是夸大了约束刚度，很可能得到不符合实际的结果，对于这类约束需要使用弹性支撑来模拟，建模复杂，且弹性支撑的刚度值不易获得。

汽车上的各种结构件通常都不是自由状态，或多或少受到约束，但是在汽车结构分析中，自由模态分析的应用范围远比约束模态分析广泛。适用于自由模态分析的结构件可分为以下三类：

第一类是受到柔性约束的结构。例如车身，在与底盘接附点处受到约束，但是接附点处是衬套等柔性件，因此约束刚度并不高，所以通常可忽略掉接附点处的约束，对车身做自由模态分析。

第二类是受到复杂约束的结构。例如副车架，在多个位置受到车身和悬架件的约束，这些约束有刚硬的，也有柔软的，而且涉及到接触、摩擦、螺栓预紧、橡胶大变形等多种非线性。对这些约束进行比较准确的模拟非常困难，所以我们通常将所有约束忽略掉，只做自由模态分析，并将计算结果与标杆副车架进行对比研究。

第三类是我们刻意忽略约束影响的结构。例如白车门，它在铰链和锁扣处都受到刚性很大的约束，进行有限元分析时，在这些位置施加适当位移约束是比较符合车门实际工作情况的。但是我们希望避开铰链和锁扣布置位置和局部结构特征的影响，考察车门整体结构设计方案。这种情况下我们仍然会选择自由模态分析，自由模态结果能够体现白车门本体的固有特性，可以根据它们来优化车门结构。

自由模态频率一定低于约束模态吗？

很多人认为约束的存在增加了结构的刚度，所以第一阶弹性约束模态的频率一定会高于第一阶弹性自由模态的频率，甚至某些正规文献中也有这样的观点。

实际上，约束的存并不是增加刚度，而是改变了结构的总体刚度矩阵。总体刚度阵的改变意味着自由状态和约束状态分别对应着不同的动力学方程系统，它们的固有频率之间没有关联，所以无法直接确定哪个高哪个低。例如图3的梁模型，自由状态下第一阶弹性模态固有频率为2582Hz，两端简支时第一阶固有频率为1414Hz，一端固支的第一阶固有频率为407.5Hz，中间两点固支的第一阶固有频率为6296Hz。可见约束模态频率可以高于自由模态频率，也可以低于自由模态频率，由具体的约束方式决定。

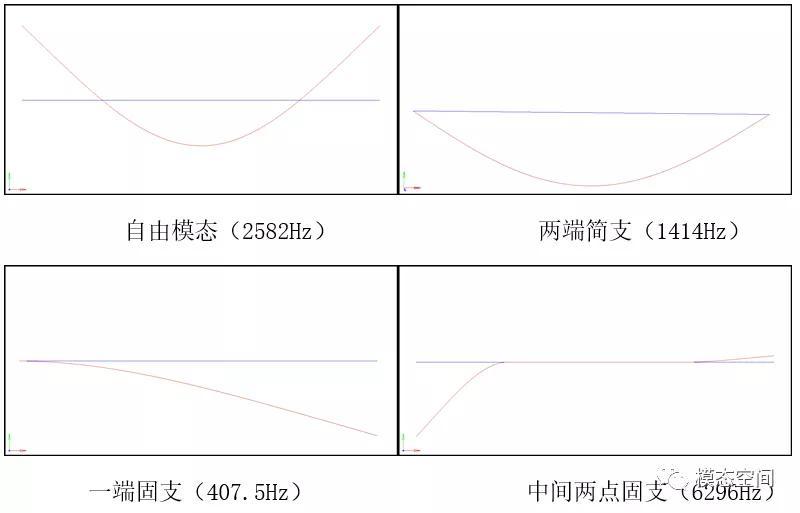
图3 梁的自由模态频率和约束模态频率

原点反之共振与约束模态

所谓反之共振，指的是在某些特定频率下的简谐激励下，结构的某些自由度振幅为0的情况。其中，在原点自由度（即在激励位置和激励方向上）发生的反之共振叫做原点反之共振。

发生原点反之共振时，结构在做简谐振动，但原点自由度响应为0。这种现象许多文献用动力吸振来解释．即外力激励将振动能量输入给原点自由度，而结构的其它自由度吸收了原点自由度的振动能量，从而使原点自由度振幅为0。其实上述说法并不正确，虽然原点受到激振力作用，但原点自由度的振幅为0，激振力做的功为0，所以根本不存在振动能量的输入。

原点反之共振时，结构没有能量输入；原点自由度受到激励力作用，但振幅为0；其它自由度未受到外界激励，进行不耗能的简谐振动。所以原点反之共振实质就是约束原点自由度的约束模态，原点所受激励力就是约束反力。

因此，原点反之共振频率就是结构在约束原点自由度之后的固有频率，通过约束模态分析就可以计算得到。

小结

• 自由模态分析可以得到刚体模态和弹性模态，前者描述结构随质心平动和绕质心转动，不产生应力；后者描述结构上各位置的相对变形，有非零应力分布。

  
  

• 任何一阶弹性自由模态振型，虽然结构变形产生了不为0的位移场分布，但结构质心位移一定为0。

  
  

• 对任意一阶弹性自由模态，针对任意一个方向，结构中都存在在该方向位移为0的点，但不一定存在XYZ向位移同时为0的点。

  
  

• 如果所施加的约束不足以控制结构在所有方向上的刚体的位移，则约束模态中仍可能有刚体模态。

  
  

• 约束模态可以视为可等效为无约束状态下的受迫振动。

  
  

• 弹性自由模态可以看做是一种特定的约束模态，位移约束恰好施加在其模态节点处。

  
  

• 受约束结构并不是必须采用约束模态分析，实际上自由模态分析的应用更加广泛。

  
  

• 第一阶弹性约束模态的频率未必高于第一阶弹性自由模态的频率。

  
  

• 原点反之共振实质就是一种约束模态。原点反之共振频率就是结构在约束原点自由度之后的固有频率。

  【免责声明】本文经授权转自模态空间，版权归原作者所有，仅用于学习！对文中观点判断均保持中立，若您认为文中来源标注与事实不符，若有涉及版权等请告知，将及时修订删除，谢谢大家的关注！