【JY】浅谈结构多点激励之概念机理(上)
简介
传统的结构地震响应分析是基于一致地震激励,只考虑地面运动随时间的变化特征,认为结构各支承处的地震动是完全相同的。而实际上地震波在传播过程中受到行波效应以及非均匀地形等地质条件的影响,场地各点的地震波动存在明显差异。
什么是行波效应?
由于传播路径的不同,地震波从震源传至两测点的时间差异导致相干性的降低,称为行波效应。

因此以一致激励对超长大跨结构进行抗震设计显然是不够精确的,需要进行多点激励地震响应分析。对于多数结构地震分析来说,使用地面加速度作为基底输入是可能的,而且产生的结构位移是相对于绝对地面位移的。在多支座输入运动的情况下,必须以不同支座处的绝对地面运动的形式来表达该问题。
根据国内外目前对于多点输入地震反应分析的研究,得到的一致结论是:一致地震动激励下的结构响应是高于或低于多点输入激励下的响应,取决于结构的动力特性、截面形式位置、反应类型以及地震动变异性的大小等。
即使是最简单的结构形式也无法确定何种激励会引起最大的响应。因此实际计算时只能针对具体的结构进行具体分析。通常情况下,应当对超长结构进行多点输入地震反应分析,这样做可以使超长结构的抗震计算更加安全合理。
地震动传播过程中对长条型或大跨度结构有什么影响呢?
(1)地震波从震源传播到两个不同测点时传播介质的非均一性效应。
(2)由于传播路径的不同,导致两测点的时间差的行波效应。
(3)由于两测点到震源的距离差异导致相干性的降低的衰减效应。
(4)由于两测点处表层土局部场地条件的差异,在传播的过程中,使两测点的地震动相干性降低的局部场地效应。
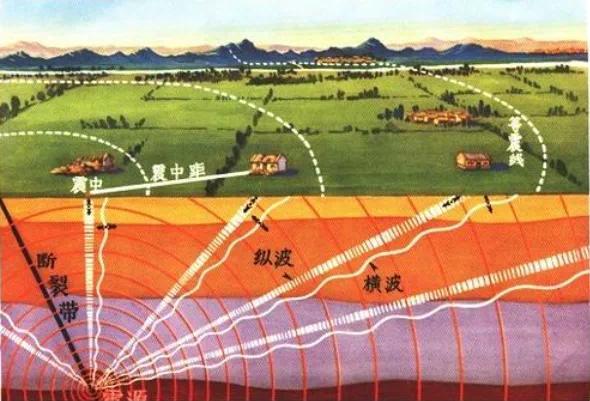
由于建筑规模所限,衰减效应影响较小,通常情况下可不考虑。根据以往的研究成果,相对于一致地面运动而言,考虑行波效应产生的计算修正占主导地位,而考虑激励点间相干性部分损失(非均一性效应,局部场地效应)产生的计算修正则小得多,而且多半是略微缩小行波效应的修正量的。
那我们应该怎么分析方法这个问题呢?
目前在进行多点输入地震反应分析时,时程分析法、随机振动分析法和反应谱方法均有所涉及,并有其各自的优势和不足。
时程分析方法虽可以考虑地震波的振幅特性、频谱特性,同时可以考虑结构的非线性特性。但由于为了体现地震荷载的随机性,必须采用多组时程进行分析,工作量较大。
随机振动分析方法是在支承点上输入地震动的自谱密度和互谱密度,由已知输入的功率谱求解输出的功率谱。但其依然存在巨大的计算量,并且目前还未达到完全实用的程度。
对于多点输入问题,由于目前长周期反应谱方面存在的问题,加上地面运动时空变化特征难以模拟等因素,反应谱方法的精度难以得到保证。
虽然时程分析方法工作量大,不妨可试试?(真香~~)
对于多支座的时程分析,采用位移加载还是加速度加载制度呢?分析过程我们该注意什么呢?
在多支座的地震输入分析中,由于采用位移荷载与加速度荷载明显不同。可使用位移荷载的地震分析,但采用位移荷载激发大量的振型。
一方面由于加速度在一个时间增量中是线性函数,而且通常平衡方程的解是精确的解。另一方面,源自线性加速度函数的位移在每个时间增量中是一个三次函数。因此,需要一个较小的时间增量,或必须使用一个更高阶的求解方法,建议采用绝对位移的加载模式。
相对位移公式中的荷载空间分布是与质量直接成比例的,通常我们用90%的模态质量参与法则可用来确保结果是准确的。然而,在基底位移输入的情况下,模态质量参与系数不能用来估算可能的误差。对于绝对位移荷载,集中力应用在结构固定基础附近的结点上。这样将激发出很多高频振型,所以需要引入可替代的误差估计,这样的做法是需要大量的振型数量,因此对于位移荷载的多点激励不建议采用振型叠加法进行分析,此时振型叠加法的振型截取可能会引起构件内力的较大误差。
对于相同的阻尼比,当指定位移输入时,与高频响应相关的有效阻尼比较大。并且,如果使用质量比例阻尼,将会因为结构的刚体运动而引入额外的阻尼。因此,如果加速度与位移分析使用相同的阻尼,将获得不同的结果。
换句话说,目前广泛使用的经典阻尼与Rayleigh阻尼所包含的质量比例阻尼在多点激励的物理意义上是不可能的。因此,如果要用现代计算机程序精确模拟承受位移荷载实际结构的真实动力性能,必须开发新的能量损耗数学模型。




