Abaqus|U形夹的拓扑优化设计
1.简介
结构优化设计是研究工程结构在满足约束条件下按预定目标(如重量最轻、造价最小等)求出的最优设计,从而降低结构成本、提高设计质量。拓扑优化是结构优化方法之一,通过以材料分布为优化对象在均匀分布材料的设计空间找到最佳的分布方案。Tosca是实现该目的的主流软件之一,已经集成在了Abaqus的优化模块中。下面通过Abaqus对U形夹进行拓扑设计来展现该设计流程。
2.问题描述
U形夹有限元模型如图1所示,约束A点的XYZ自由度,约束B点Y自由度,C点和D点分别施加方向相反的集中力,大小为100N。其材料为1mm厚的铜材:密度8.82e-9t/mm3,弹性模量为131e3MPa,泊松比为0.34,屈服强度为473MPa,极限强度为816MPa。
优化目标:最小化体积;
约束条件:C和D点的绝对值位移小于0.1mm;
设计变量:设计区域的单元密度。
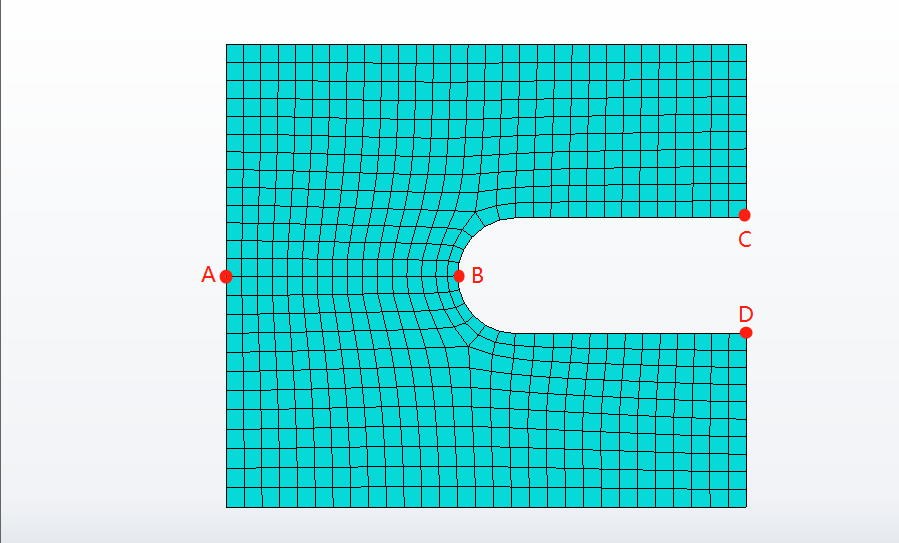
图1 C形夹有限元模型
3.技术路线
本节首先进行了U形夹的初始设计分析;然后,对U形夹进行了拓扑优化。
3.1初始设计分析
通过建立图1有限元模型并提交分析,图2所示为初始的位移和应力云图。其中在C、D处的位移最大,为0.088mm。由应力云图可知,在结构蓝色云图处应力值几乎为零,对结构强度并无贡献,这也正是需要拓扑优化删除的区域。
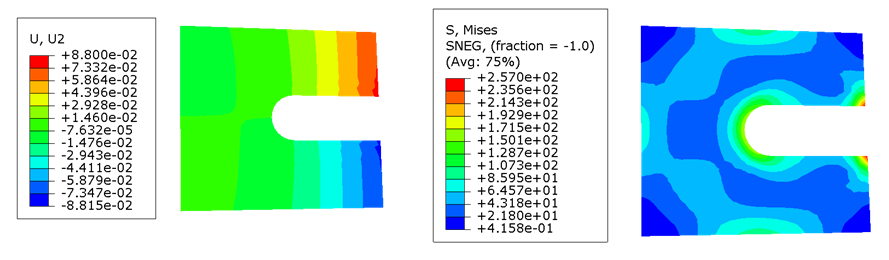
图2 初始位移、应力云图
3.2拓扑优化设置
针对3.1中的有限元模型,CAE界面切换到优化模块进行优化设计。
1、 创建优化任务
选择拓扑优化,勾选如图3所示的红色线框内容,完成优化任务的创建。
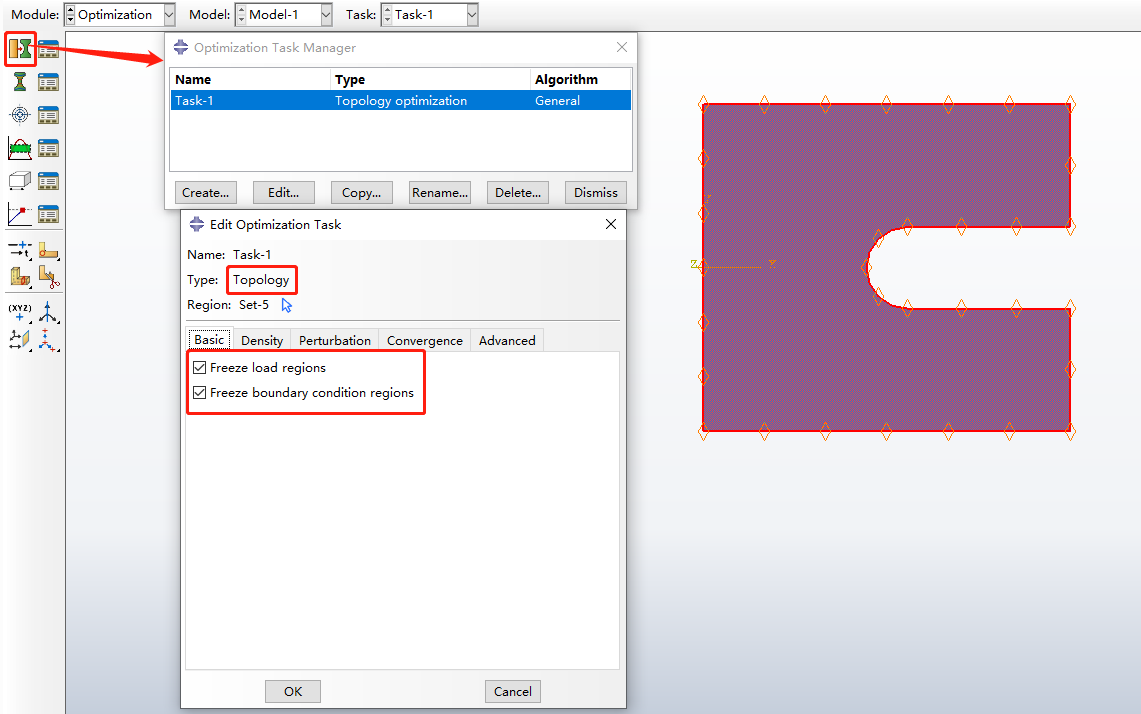
图3 创建优化任务
2、 创建设计响应
图4展现了创建的设计响应,分别为C、D两点的位移以及整个模型的体积。
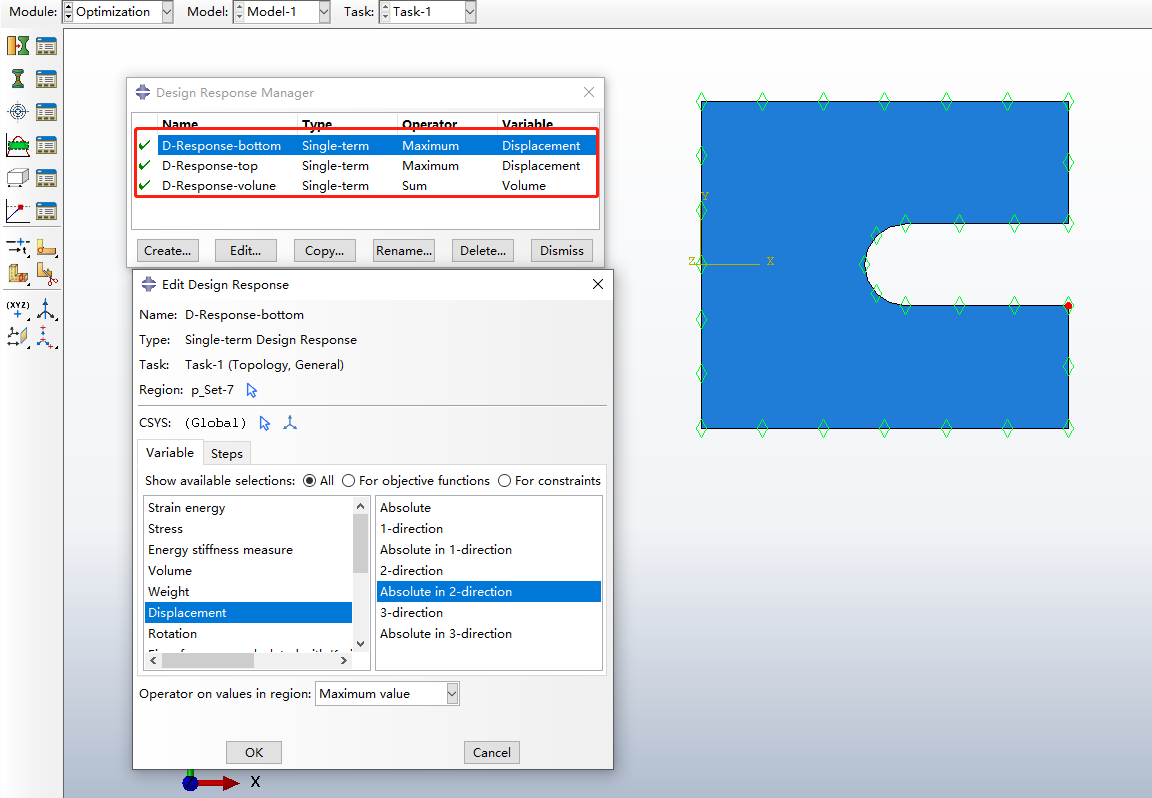
图4 创建设计响应
3、 创建目标函数
体积最小化的目标函数在这一步被设置了,如图5。
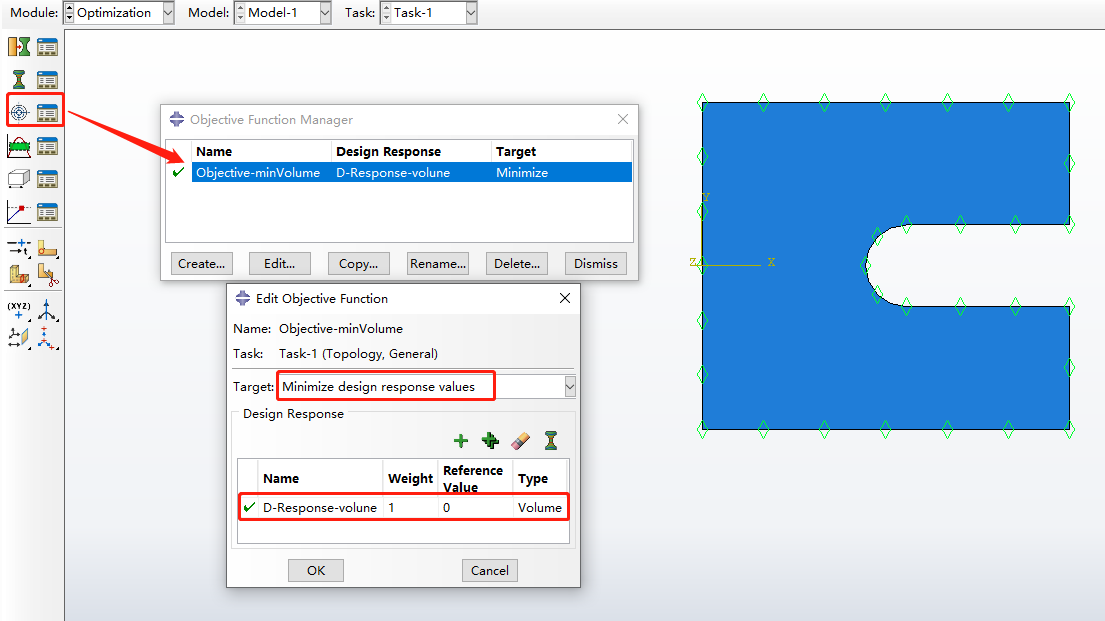
图5 创建目标函数
4、 创建约束
图6为创建的约束情况,其中C、D两点的最大位移小于0.1mm。
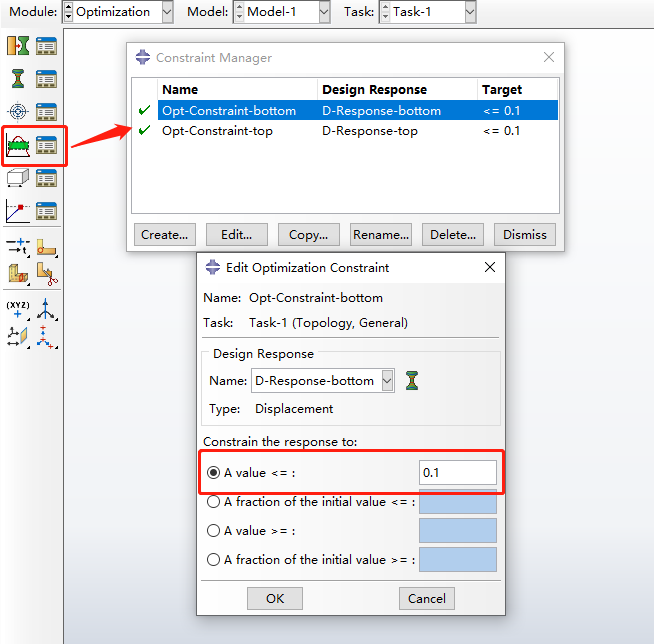
图6 创建的约束
4.优化结果
图7-8分别为拓扑优化第12次优化结果和最终优化结果。不难发现,随着优化次数的增加,拓扑优化达到收敛结构的最佳形状。对比图2初始分析时的结构,拓扑优化的结果是挖掉了初始分析中应力值接近零的蓝色的区域,因为这一部分对结构的强度没有影响。同时,经过拓扑优化,优化结构的最大应力相比于原始结构减少了60MPa。因此对构件进行合理的优化设计,不仅可节省材料还能增加结构的承重能力。
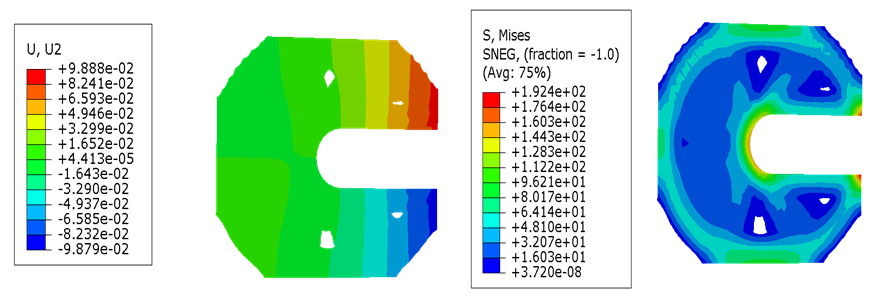
图7 迭代12次的结果
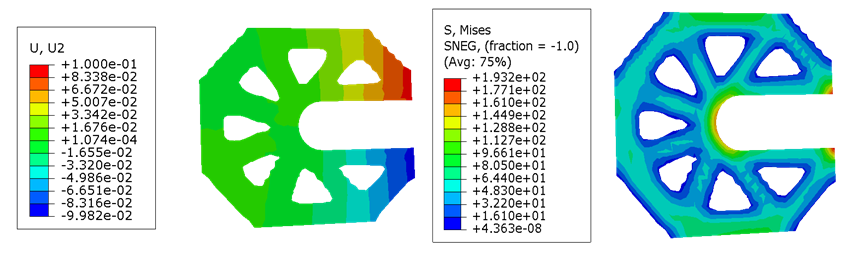
图8 迭代30次的结果




