【JY】基于Ramberg-Osgood本构模型的双线性计算分析
本文摘要(由AI生成):
FNA(快速非线性分析方法)用于结构系统的静力与动力分析,通过减少求解规模并迭代计算非线性单元力,比传统方法快几个数量级。FNA已加入SAP2000程序,能计算并绘制总输入能量、应变能量等,并评估时间步长。该方法适合设计或改型抗震结构,结合不同类型的非线性单元使用。算例对比显示SAP2000的HHT算法下滞回曲线耗能效果最显著,与Matlab和OpenSees结果基本一致。
很多实际结构都有有限数量的点或构件,当承受静力或动力荷载时,在这些点和构件上就会产生非线性行为。斜撑的局部屈曲、基础的隆起、结构不同部分之间的接触以及某些单元的屈服,都是具有局部非线性行为的结构范例。对于动力荷载,常见的做法是添加集中阻尼、基础隔震和其他耗能单元。在多数情况下,这些非线性单元易于确定,对于其他结构,则需要进行初始弹性分析来识别非线性区域。
主要计算方法(非线性方法仅在线性方法中迭代Newton—Raphson法)请看上一期:
【JY】结构动力学初步-单质点结构的瞬态动力学分析
小编今天带大家看新东西——FNA法。FNA(Fast Nonlinear Analysis Method,快速非线性分析)方法将应用于线性或非线性结构系统的静力与动力分析。假定存在有限数量的预定义非线性单元,采用弹性结构系统与刚度和质量正交的、荷载相关的Ritz向量,来减少要求解的非线性系统的规模。在每次迭代或加载步骤结束时,非线性单元中的力用迭代法进行计算,对每个时间增量都可准确地求解出非耦合模态方程。
所谓的FNA快速非线性分析方法,是与一般计算速度与非线性分析的传统方法进行了比较,后者采用了在每个荷载增量时形成完全的平衡方程并进行求解。对于许多问题,FNA方法要快几个数量级。
FNA方法是一种简单方法,这种方法能满足基本力学方程(平衡、力——变形和协调性)的要求。在时间t处,结构计算机模型的精确的动力平衡方程。

如果没有非线性单元计算机模型不稳定,则可在非线性单元的位置添加任意刚度的“有效弹性单元”。如果在方程的两边加上有效力[Ke]{u},则精确的动力平衡方程可写为

再通过模态叠加法进行求解该方程,达到事半功倍的效果。
FNA 方法已经添加到用于通用目的的结构分析程序SAP2000中。SAP2000计算机程序通过把模态阻尼和非线性单元作为时间函数来计算并绘制总输入能量、应变能量、功能和能量的损耗。除此之外,能够计算出能量误差,我们可以评估适当的时间步长。因此,这种能量计算的功能可以对不同的结构设计进行比较。在大多数情况下,对于特定动力荷载的优秀设计是在结构系统内吸收最少应变能的设计。
与进行标准线性振型叠加分析的情况一样,我们可以使用多次分析来核对是否已经使用了足够小的时间步长和适当的振型数。此途径将确保这种方法收敛到精确解。
许多不同类型的实际非线性单元可与快速非线性分析(FNA)方法结合使用。FNA方法对于设计或者改型抗震结构都是非常有效的,因为该方法的目的就是要对具有一定数量的、预先定义的非线性或能量消散单元的结构进行高效计算。这与地震工程学的现代理念是一致的,即在大地震后耗能单元应该能够进行检查和更换。
基础隔震器是用于抗震设计的最常用的预定义非线性单元类型。除此之外,隔震器、机械阻尼器、摩擦装置和塑性铰是另外一些常用的非线性单元类型;另外,还需要间隙单元来模拟结构构件与结构上抬之间的接触;一个具有挤压和耗能能力的特别类型的间隙单元对模拟混凝土与土壤的相互作用是非常有用的;只受拉力并且在屈服中损耗能量的单元多用于桥梁类型结构上。
Ramberg和Osgood(1943年)首先提出了钢材的三参数应力-应变关系曲线,即著名的Ramberg-Osgood曲线。RO模型常被用于描述刚度退化模型,RO模型由骨架曲线和滞回曲线组成,骨架曲线的表达式为:
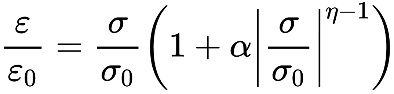
则滞回曲线表达式为:

RO模型的力与位移关系式为:

滞回曲线面积也就是一个周期内消耗的能量为:



例题
为了对比各软件与理论计算结果的误差和展示建模过程,以一个简单的单质点体系作为算例,地震波选取三条人工波,单质点体系的m=100kg,屈服后刚度是541.5N/m,屈服前是13倍,屈服力100*9.8*0.2N,提取质点的加速度、位移时程及滞回曲线进行对比。


为了对比简洁以下结果仅呈现RGB1的计算结果。
Sap2000模型中分别以:直接积分方法中的Newmark、Willson、HHT算法和FNA法分析,其中等效刚度分别采用屈服前刚度k1和屈服后刚度k2计算。



OpenSees



Matlab
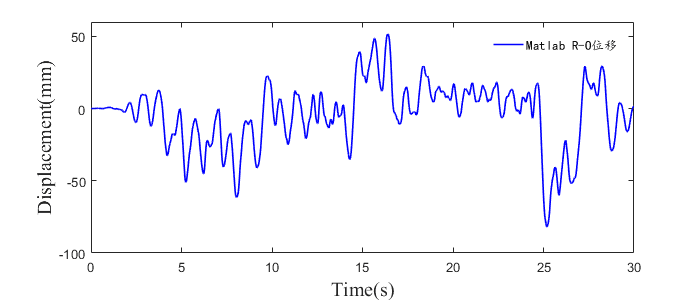
Mat:基于R-O模型双线性


Mat:双线性模型双线性



对比结果:



结论:
1 .SAP2000各种模型分析结果可知:各种算法下的加速结果基本一致,HHT 算法下的位移最大,同样的,HHT算法下的滞回曲线耗能效果最为显著;
2 .Matlab R-O、Matlab 双线性滞回 、OpenSees和SAP2000 计算结果基本吻合,与上述结论一致,SAP2000 HHT算法下的滞回曲线耗能效果最为显著。




