【JY】板壳单元的分析详解
本文摘要(由AI生成):
本文讨论了工程模拟中板构件的边界效应、分类以及在不同软件中的模拟方法。板的边界效应需通过细化网格来体现,且板可根据其厚度与宽度的比值分为厚板、薄板和薄膜。SAP2000/Midas软件中的板壳对象分为膜单元、板单元和壳单元,各自具有不同的力学特性。通过算例A对比了基于不同假设(Kirchhoff和Mindlin-Reissner)的壳体模拟结果,发现薄壳在较厚板时失真。算例B则区分了SAP2000中壳、板和膜单元的平面内外刚度特性,强调了壳单元作为完全单元的优势。文章强调了理解板构件力学特性的重要性,并期待后续内容的深入讨论。
简介
板壳是平板和壳体的总称,是最常见的物体形式。其外形特点是厚度比其余两个方向尺寸在数量级上小得多。平分物体厚度的分界面称为中面。若中面是平面,则称此物体为平板;若中面是曲面,则称此物体为壳体。(注意,此处和软件中的板单元、壳单元非同个概念)
为什么要研究板壳单元?
由于厚度小、质量轻、耗材少、性能好,使板壳成为具有优良特性的结构元件,不仅广泛应用于各种工程结构作为最基本和最主要的构件,而且在自然界和日常生活中也常常碰见,它们与每个人的生活休戚相关,与人类的生存紧密相连。
人们希望建立一种这样的板弯曲单元,即厚薄板通用单元。这将为工程计算与理论研究带来极大的便利。希望建立一种单元,同时又希望当厚度趋向薄的情形时,该单元的解也能趋于薄板的解。表面上,这对有限元法而言,容易实现,而实际上,当厚度趋于零时,并不能收敛于薄板数值解,出现所谓的剪切闭锁现象。(剪切锁死(shear locking),简单地说就是在理论上没有剪切变形的单元中发生了剪切变形,该剪切变形也常称伴生剪切。)
板壳单元分析的历史
板壳结构的分析的故事起源于18世纪,Euler最先探索了板的弯曲问题。1850年,Kirchoff给出了第一个完善的薄板弯曲理论,接着Aron(1874)做了薄壳的分析工作。1945年Reissner放松了Kirchhoff假设,考虑了横向剪切变形的影响,因而,使其能够应用于中厚板壳,随后Mindlin(1951)也以略为不同的方式放松了该假设。
1977年,Hughes首先提出基于Mindlin理论的双线性四节点四边形板单元。该单元考虑横向剪切效应,因此适于中厚板,同时若选择适当的高斯积分点,亦可分析薄板问题。但是当板较厚时,由于存在零能模式使计算结果出现震荡,为此Hughes提出修正积分法。(零能模式(zero-energy mode):采用一阶减缩积分时会出现零能模式,即单元只有一个积分点,在受弯时该积分点没有任何的应变能,此时此单元没有任何刚度,就无法抵抗变形。)
板壳结构是三维实体结构的特殊形式,为了简化求解,远在实体单元可行之前,就引入了几种经典的假设对板壳单元进行计算,其中以Kirchhoff假设和Reissner-Mindlin假设的两类板壳理论最为常用。
Kirchhoff (基尔霍夫) 薄板壳理论
基于Kirchhoff假设的经典薄板壳理论,忽略了剪切变形的影响,常适用于薄板壳结构分析;
Kirchhoff理论的基本假设有三个:
(1)平行于壳中面的各层互不挤压;
(2)直法线假定:变形前垂直于中面的直线段,在变形后仍保持为直线且垂直于变形后的中面,这相当于忽略横向剪切变形;
(3)中面内无平行于中面的位移。
基于上面的假定,我们可以理解为板上的直线元最初垂直于中面,变形后它仍然垂直于变形后的中面;中面上的所有纤维是不可伸长的。从上可以得到通过该理论来推出这个薄变形体的近似数学理论,如果薄板任一部分的线性尺寸和截面尺寸的大小是同一数量级的,那么一般弹性力学方程在它的任何一个微小部分都适用。这段薄板的运动方程可以由其变形运动学的一阶近似简化得到。
Reissner-Mindlin (瑞斯纳-明德林) 中厚板壳理论
基于Reissner-Mindlin假设的中厚板壳理论,则考虑了剪切变形的影响,适用于中等厚度的板壳结构分析。
(注意:很厚很厚的实体块(如坝体),可用实体单元,也可视问题简化采用平面应变/平面应力)
Mindlin/Reissner 理论的基本假定是:
(1)与壳的厚度相比,位移是微小的;
(2)垂直于中面的应力忽略不计;
(3)变形前垂直于中面的直线,变形后仍保持为直线,但不一定再垂直于中面;
(4)挠度和法线转角为各自独立的场函数。
经典的板壳理论是基于Kirchhoff假设的,忽略了横向剪切变形对板、壳变形的影响,能很好的处理薄的板壳问题,但随着厚度的增加,会产生很大的误差。可见Mindlin/Reissner 壳保持了一些Kirchhoff壳的特点,但由于不忽略剪切变形,使变形前垂直于中面的直线变形后不再垂直于中面,转角变形中应包括非均匀的平均剪切变形。
Mindlin/Reissner 理论其中比较典型的有三种:①Reissner理论;②Mindlin理论;③高阶剪切变形理论。
Reissner首先采用直线假定,认为变形前垂直于中面的直法线变形后仍为直线,但不再为法线,以代替Kirchhoff假定中的直法线假设,考虑了横向剪切变形的影响,同时计及了法向应力和应变的影响,采用Lagrangian乘子的变分法导出基本方程。之后Mindlin发展了Reissner理论,该修正理论的应用领域扩至厚板壳,我们将其称为Reissner-Mindlin板壳理论,亦为一阶剪切变形理论。

Reissner-Mindlin横截面假设
理论小讲
(详细的可学习下《板壳理论》相关书籍):
①直法线假设,即原来垂直于薄板中面的一段直线在板弯曲变形时始终垂直于薄板中面且保持长度不变。这意味着不考虑横向剪切变形和挠度沿板厚的变化,即

式中:z是垂直于板面的坐标方向。由z向应变为0可得到:

②薄板中面没有面内位移,即在中面内有


根据Kirchhoff假设,板面上任何一点的面内位移u和v为:

因为薄板的面外应力分量远小于面内应力分量,所以在薄板理论中采用平面应力问题的物理方程(注意平面应力问题的基本假设),于是有

由弯矩和扭矩的定义可知,沿板厚积分(辛普森/高斯积分)即可得弯矩和扭矩与曲率和扭率的关系,得:![]()
其中,
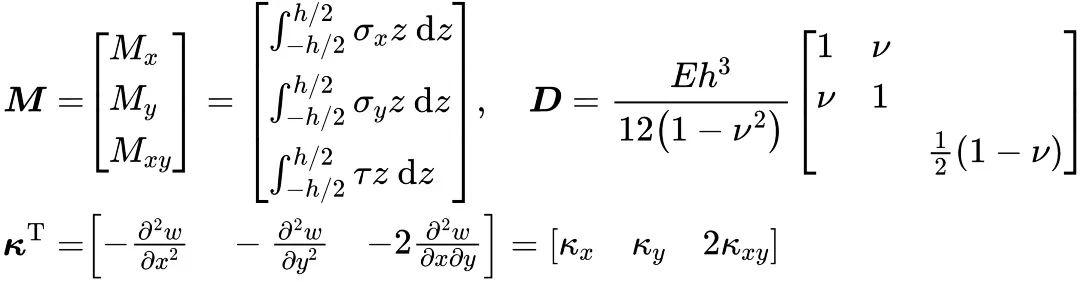
上式是薄板广义应力M与广义应变K的关系,或称薄板的本构关系。
在薄板理论中不考虑横向剪切变形,故作用在单位宽度上的剪力是根据微元的平衡条件求出的,即

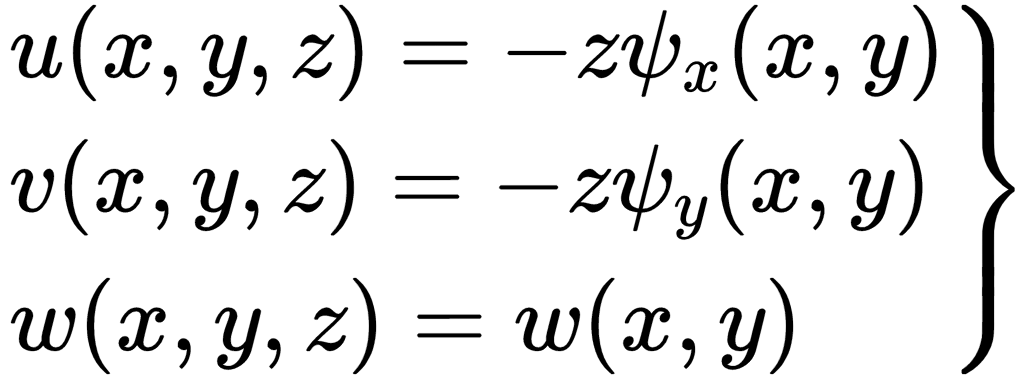
沿厚度方向积分的弯矩与曲率关系为:![]()
式中曲率的定义与薄板情况不同,此处定义为:
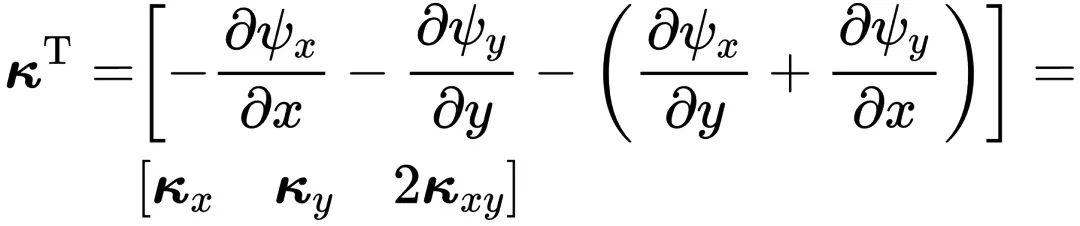
在剪切板理论中,由于放松了直法线假设,因此出现了如下两个剪切变形,即

与薄板不同,剪切板的剪力可直接利用物理方程导出为

式中:k是剪切修正系数,当材料沿板厚均匀分布时,通常k=5/6(矩形截面),也有人用k=pi^2/12。弯矩和剪力与应力的关系与薄板的情况完全相同。
值得指出的是,厚板理论存在边界效应。比如,厚板理论自由边的剪力为零,若考察剪力从板中央到自由边的变化过程,就会发现在自由边附近剪力急剧减小为零,这就是厚板的边界效应。随着板厚度的减小,这种效应会越来越剧烈,因此,对于板的自由边,综合剪力等于等于零更为合理。在板的固支和简支边界上也会存在边界效应现象。为了能够在有限元方法结果中看到边界效应,需要细化边界附近的网格。
工程模拟问题讨论
在工程结构中,板是一种常见的构件,其几何特征是:一个方向的几何尺寸远小于另外两个方向的尺寸。即厚度H远小于长度L与宽度B(一般L≥B)。根据厚度与宽度的比值范围可将板分为厚板、薄板与薄膜,通常可定范围为(注意,更多时候会根据受力的特征来定义 薄/厚 板/壳/膜):
厚板为 H/B ≥ 1/8~1/5;
薄板为 1/100~1/80 ≤ H/B ≤ 1/8~1/5;
薄膜为 H/B ≤ 1/100 ~1/80。
通常把板作为抵抗弯扭的结构件,但厚度非常小的板(如薄膜)抵抗弯扭的能力较差,可以认为其抗弯刚度近似为零,面内和面外载荷皆由中面内力来平衡,即薄膜可以看做是弦的二维扩展。同样,薄板可以看做是欧拉梁的二维扩展。对于薄板小挠度理论,采用Kirchhoff假设与平面应力的本构关系。中厚板采用Mindlin-Reissner假设与平面应力的本构关系,但放松了变形后直线与中面垂直的条件,这可视为剪切梁的二维扩展。
SAP2000/Midas中,均为弹性壳小挠度分析,其中薄字代表Kirchhoff假设,如薄壳、薄板;厚字代表Mindlin-Reissner假设,如厚壳、厚板。
在SAP2000中,板壳对象按照受力特点可以分为三类:膜单元、板单元及壳单元(另外两类暂不在讨论:平面应力单元、平面应变单元)。
膜单元只具有平面内的刚度,承受膜力,建筑结构中楼板通常用膜单元来模拟;
板单元的行为与膜单元相反,只具有平面外的刚度,承受弯曲力,模拟薄梁或者地基梁等;
壳单元的力学行为是膜单元与板单元之和,是真正意义上的壳单元。也可以根据中面的形状划分:如果壳的中面为平面,则壳的薄膜应力和弯曲应力状态互不耦合,而壳的中面也可为曲面,此时薄膜应力与弯曲应力耦合。
在ABAQUS/Standard中,一般的三维壳单元有三种不同的单元列式:一般壳单元、薄壳单元和厚壳单元。一般壳单元考虑了有限的膜应变和任意大的转动,薄壳单元和厚壳单元考虑了任意大的转动,但是仅考虑了小应变。一般壳单元允许壳的厚度随单元的变形而改变,而其他的壳单元仅假设单元节点只能发生有限的转动。壳单元库中有线性和二次插值的三角形、四边形壳单元,以及线性和二次的轴对称壳单元。所有的四边形壳单元(除了S4)和三角形壳单元S3/S3R采用减缩积分。而S4和其他三角形壳单元采用完全积分。
【算例A】
给一块边长为跨度为十米的板,面荷载为100N/m2,对比基于Kirchhoff假设和Mindlin-Reissner假设的差别来讨论完全壳单元的力学性能。
材料和积分点设置如下图:


Abaqus实体(对照)-Abaqus壳体-Sap2000厚薄壳-Midas厚薄壳 :
(注意此处Abaqus壳体为Mindlin-Reissner假设壳体)
厚度为100mm


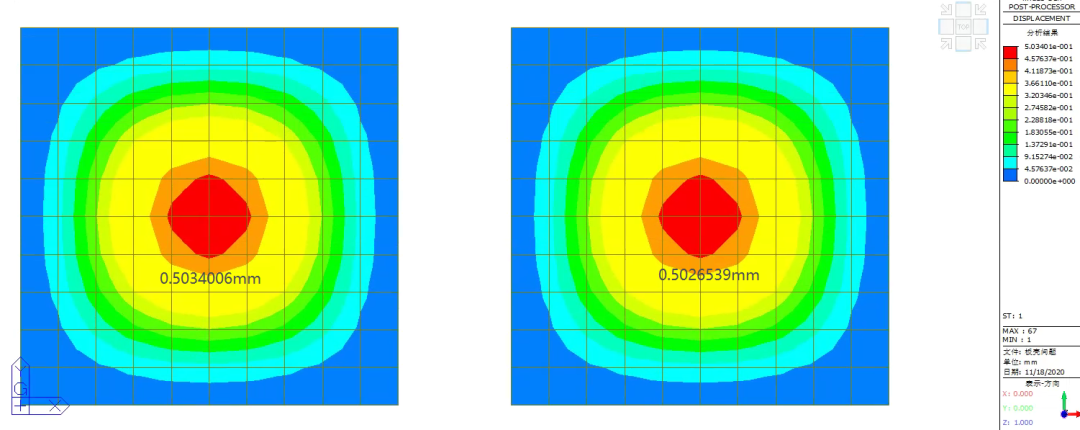
板厚为100mm,左厚壳/右薄壳
厚度为500mm

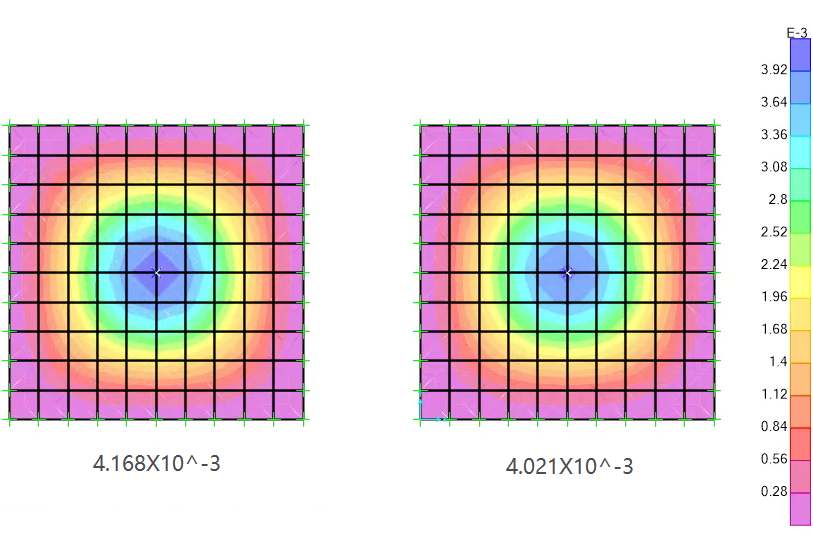

板厚为500mm,左厚壳/右薄壳
厚度为1000mm



板厚为1000mm,左厚壳/右薄壳

厚度为2000mm

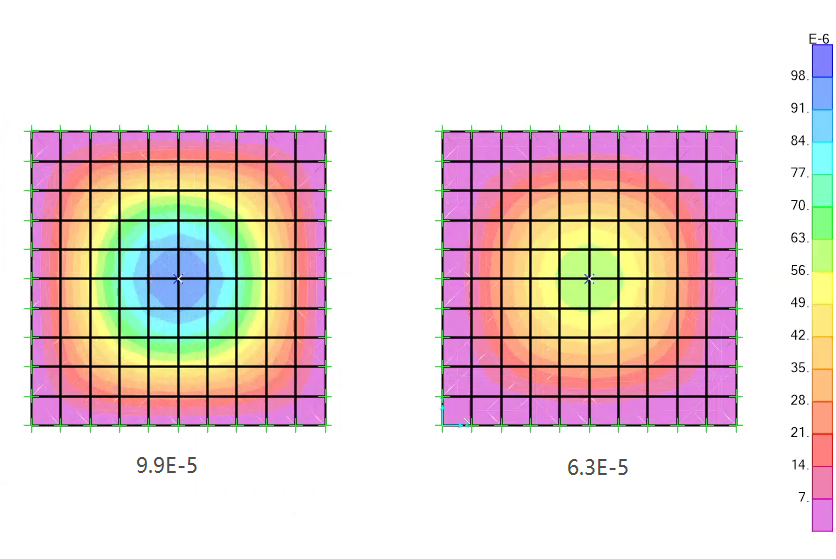

板厚为2000mm,左厚壳/右薄壳

可见在边长为10mX10m时,板厚为1000mm厚时,薄壳已经失真。
【算例B】
区别Sap2000里壳/板/膜 的平面外刚度/平面内刚度。
在Sap2000中,壳单元具有面内外刚度,是完全单元,板/膜单元仅为壳单元的特例。
板单元仅具有平面外刚度,可模拟承受弯曲力,在需要且假设得当的情况下,可模拟薄梁或者地基梁等。
膜单元仅具有平面内刚度,可模拟承受膜力,在需要且假设得当的情况下,可模拟建筑楼板。
壳面内外均能受力:

板面外能受力,面内数值巨大无比已经失真:

膜面内能受力,面外数值巨大无比已经失真:

概念为先,机理为本,请看下篇!
建源之光——工程侠




