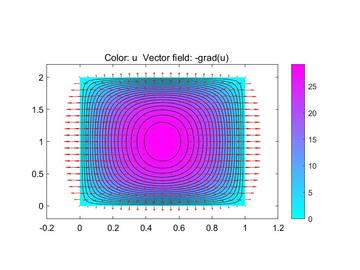
实例演示特征方程求解

过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载,qq:927550334
![]()
最近在学习过程中,过冷水经常会接触到以下关系式
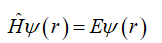
懂得人自然懂,该关系式其实就是薛定谔方程,该等式其实很有特点,我高等数学中的特征方程和形式一致,本期过冷就和大家学习一下解特征方程问题,用Matlab轻松解薛定谔方程。
在学习线性代数过程中,肯定都有特征值与特征向量的概念,先和大家温习一下特征值和特征向量概念。
设A为n阶矩阵,存在可逆矩阵P=(α1,α2,...,αn)使得以下关系式成立
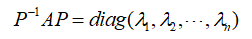
对上述等式进行改写
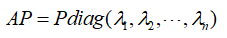
则α1为A的特征向量,λ1 为对应的特征值。那么如何解 Aα=αλ 这个方程?
线性代数中将Aα=αλ 改写成(λE一A)α=0,这说明对于λ,方程组(λE一A)x=0有非零解,α就是方程组(λE一A)α=0一个非零解。反之,若齐次线性方程组(λ0E一A)x=0有非零解α0 ,则数λ0是A的特征值,α0是A的属于特征值λ0的特征向量.这就是说数λ是A的特征值当且仅当齐次线性方程组(λE一A)x=0有非零解.而齐次线性方程组(λE一A)x=0有非零解的充分必要条件是|λE一A|=0.因此数λ是A的特征值当且仅当|λE一A|=0.定义理解起来好抽象,过冷水给大家举一个简单一点案例。
给出矩阵A,求对应对应的特征值和特征向量。
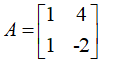
则A特征方程为

A的特征值为 λ1=-3,λ2=2,
A的属于λ1=-3特征向量是线性方程组(-3E一A)x=0即:
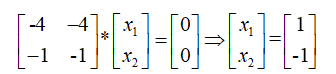
A的属于λ2=2特征向量是线性方程组(2E一A)x=0即:
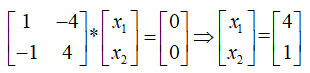
一般在解决实际问题的时候,我们不可能用手算,工作量太大了,可以使用Matlab函数完成特征方程求解。
[V,D] = eig(A) 返回特征值对角矩阵 D 和矩阵 V,其列是对应右特征向量,使得 A*V = V*D。
A=[1 5 8;7 5 9 ;4 4 8] [V,D] = eig(A) N=V*D M=A*V A = 1 5 8 7 5 9 4 4 8 V = -0.4871 -0.8048 -0.1517 -0.6921 0.5888 -0.8344 -0.5327 0.0757 0.5299 D = 16.8540 0 0 0 -3.4107 0 0 0 0.5567 N = -8.2092 2.7448 -0.0844 -11.6643 -2.0081 -0.4645 -8.9783 -0.2583 0.2950 M = -8.2092 2.7448 -0.0844 -11.6643 -2.0081 -0.4645 -8.9783 -0.2583 0.2950
而对于这样文章开头提到的薛定谔方程该如何求解?
在此给大家一个比较简单的案例,薛定谔方程借鉴的矩阵特征方程形式,实际不是矩阵运算,
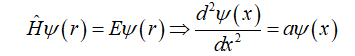
可以解得:
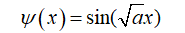
关于微分方程问题 偏微分方程数值详讲 偏微分工具箱求解热导方程实例演示中有做详细叙述,在此过冷水就不做详细讲解,本期只是给大家普及一下特征方程和特征向量概念,以及具体使用技巧,是实际应用中 eig(A)的用法很多,过冷水在后期会一一和大家讲解。

过冷水发表于 仿真秀 平台原创文章,未经授权禁止私自转载,如需转载请需要和作者沟通表明授权声明,未授权文章皆视为侵权行为,必将追责。如果您希望加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载均可加群:927550334。
精品回顾
过冷水和你分享 matlab读取存储各种文件的方法 文末有独家金曲分享