华北电力大学龙凯博士:基于Matlab四边形等参元有限元分析(8月12日)
文章亮点
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐


导读:当前,新冠肺炎疫情在国内呈现多点散发、局部暴发的态势。笔者居住的北京市也连续出现多例京外关联本地确诊病例。所幸的是,截至8月9日24时,北京市已连续5天无新增京外关联本地病例及感染者报告。受仿真秀平台的邀请,自8月12日起,给居家的理工科学子免费带来暑期拓扑优化学习班(8月12日-31日)详情见后文。
以下内容是我拓扑优化学习班第一期直播《四边形等参元有限元分析与Matlab程序编制》授课PPT,欢迎大家踊跃报名。直播PDF和程序在附件下载!
一、平面问题的由来
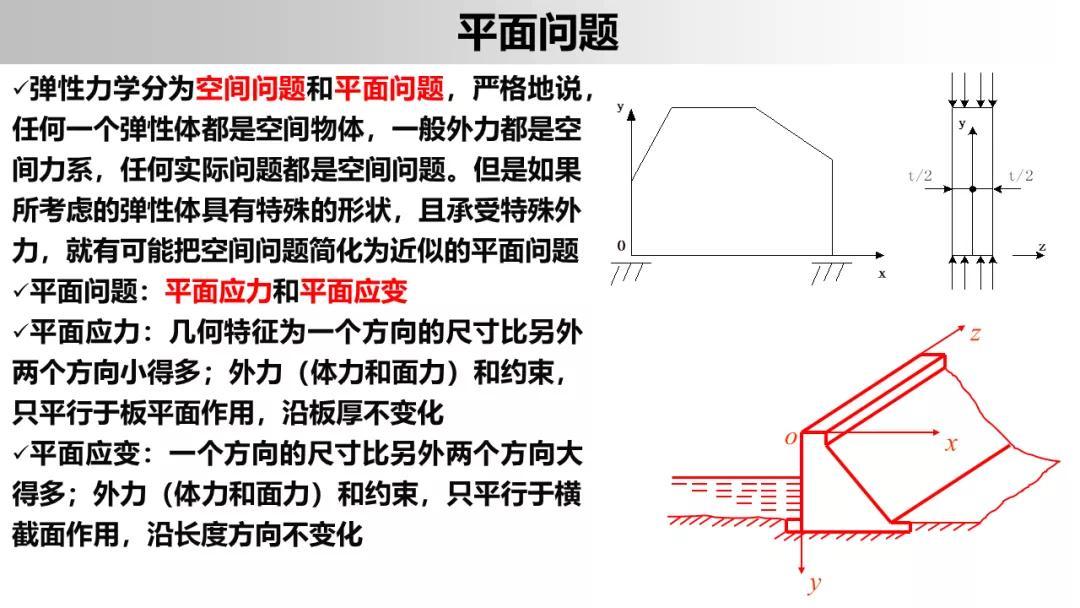
众所周知,弹性力学分为空间问题和平面问题,严格地说,任何一个弹性体都是空间物体,一般外力都是空间力系,任何实际问题都是空间问题。但是如果所考虑的弹性体具有特殊的形状,且承受特殊外力,就有可能把空间问题简化为近似的平面问题
平面问题:平面应力和平面应变
平面应力:几何特征为一个方向的尺寸比另外两个方向小得多;外力(体力和面力)和约束,只平行于板平面作用,沿板厚不变化
平面应变:一个方向的尺寸比另外两个方向大得多;外力(体力和面力)和约束,只平行于横截面作用,沿长度方向不变化
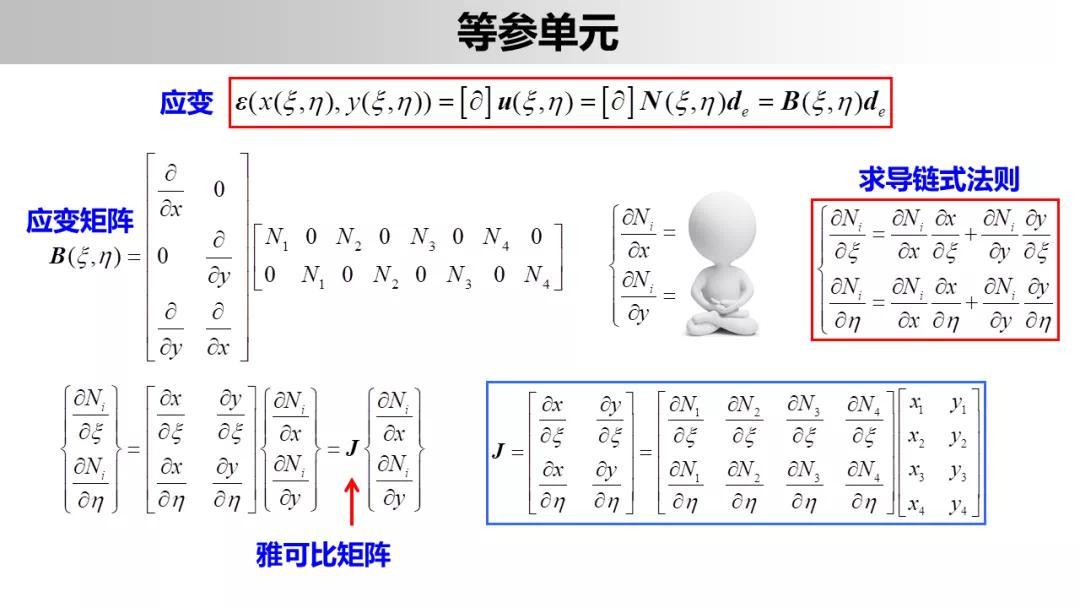
二、等参元的引入
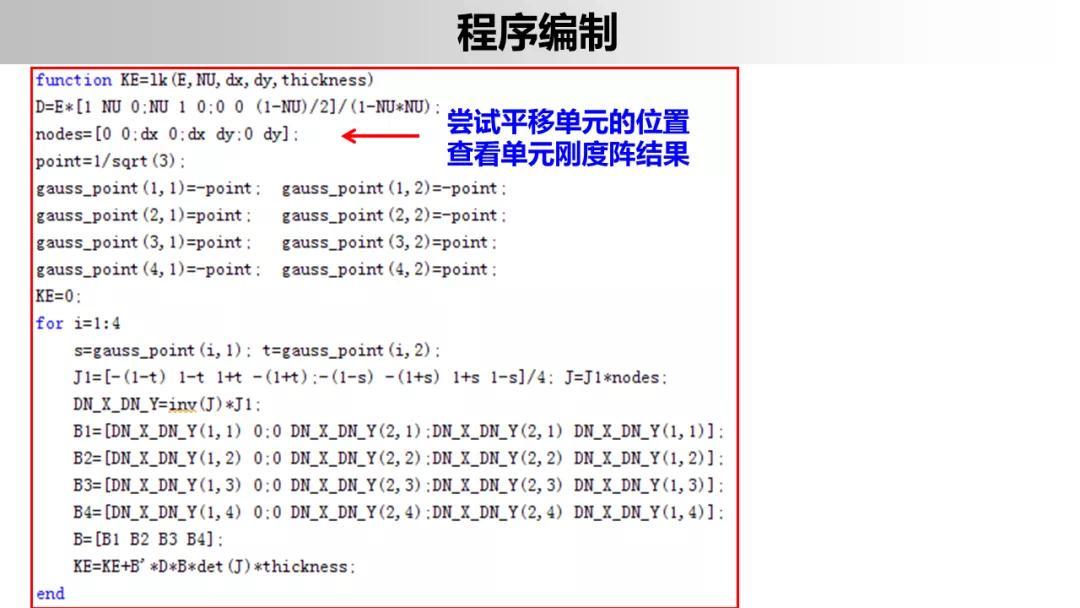
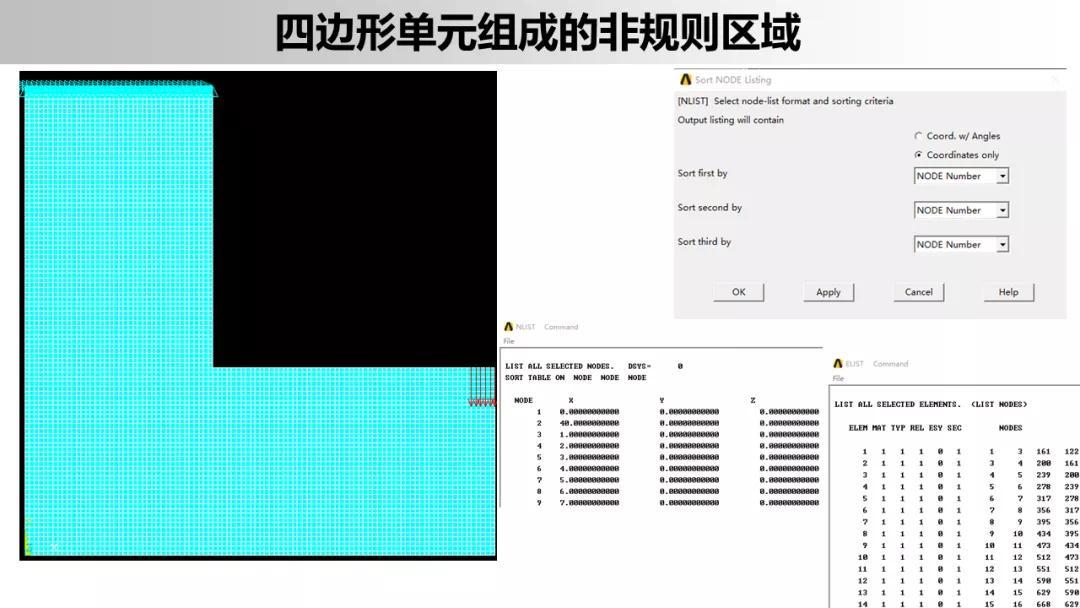
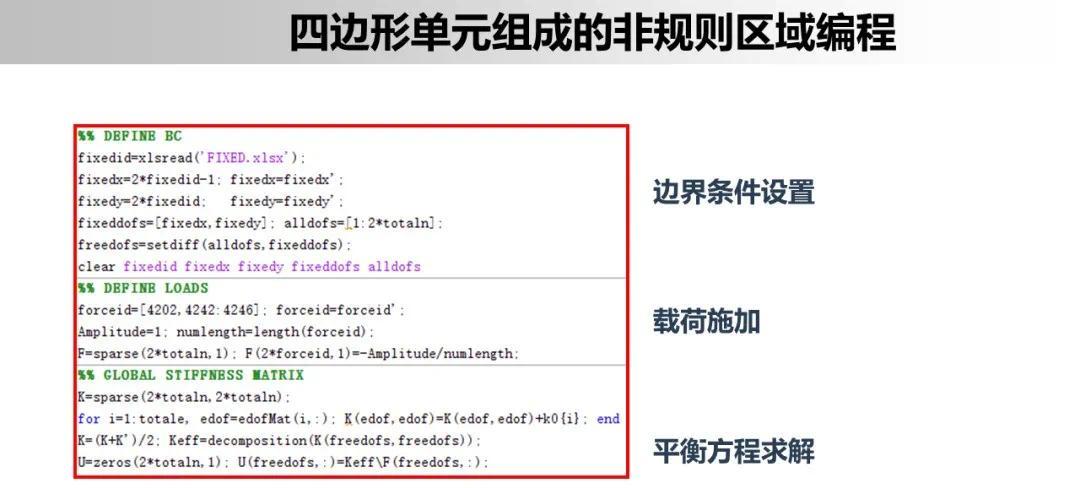
对于一般的四边形单元,在总体坐标系下构造位移插值函数,则计算形状函数矩阵、单元刚度矩阵及等效节点载荷列阵时十分冗繁;而对于矩形单元,相应的计算要简单的多。
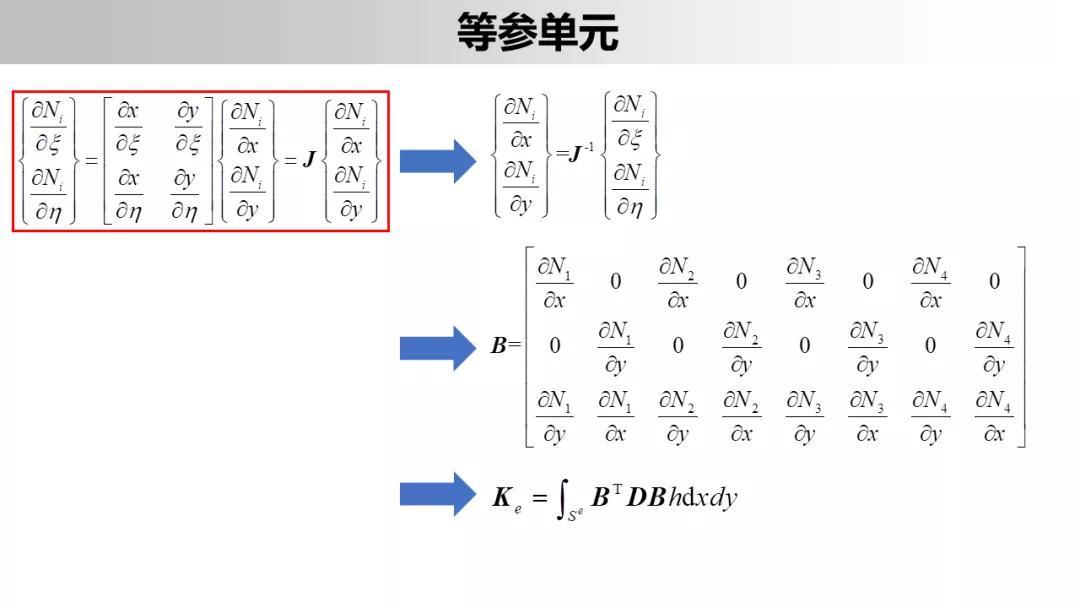
矩形单元明显的缺点是不能很好的符合曲线边界,因此可以采用矩形单元和三角形单元混合使用(网格划分困难)。更为一般的方法是通过等参变换将局部自然坐标系内的规格化矩形单元变换为总体坐标系内的任意四边形单元(包括高次曲边四边形单元)
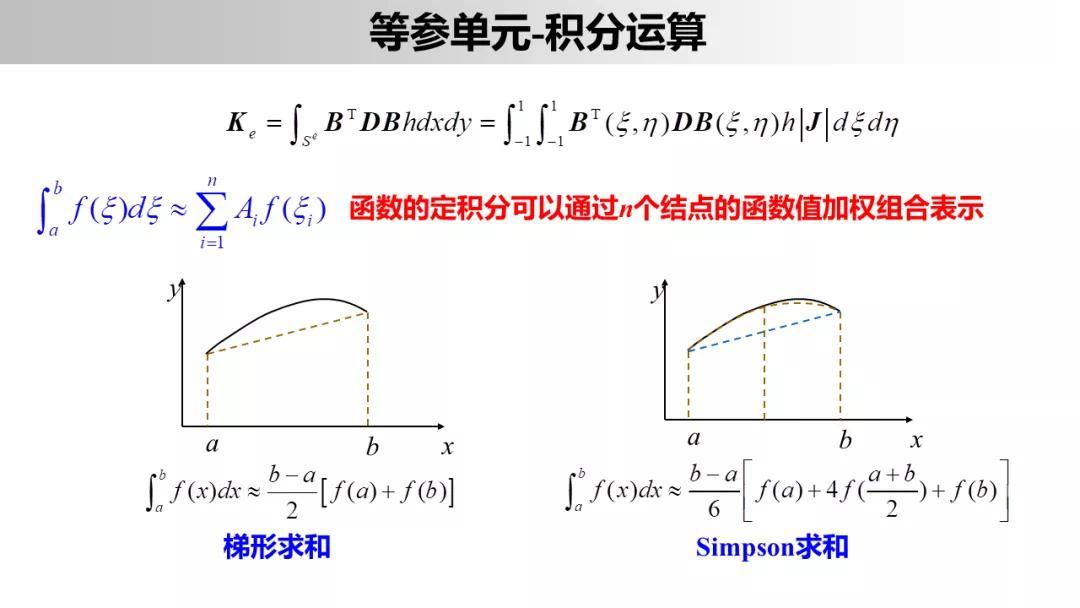
等参单元的提出,为有限元法成为现代工程实际领域最有效的数值分析方法迈出了极为重要的一步。














(完)
登录后免费查看全文
附件
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2021-08-12
最近编辑:3年前
作者推荐
还没有评论
相关推荐
最新文章
热门文章





