【一文看懂】瞬态响应跟稳态响应(谐响应)的关系
本文摘要(由AI生成):
本文介绍了结构动力学中瞬态响应与频率响应的关系。首先介绍了结构动力学问题可以在时域或频域下求解,并介绍了频率响应分析方法。接着通过一个单自由度弹簧质量系统的案例,介绍了瞬态响应与频率响应的关系。在瞬态响应分析中,系统在载荷作用下会有一个“适应”过程,之后会趋于稳定。通过瞬态响应分析找到的稳态幅值与频率响应结果刚好吻合,解释了频率响应结果的物理意义。频率响应分析可以反映出系统的固有振动特性,方便与试验对标,验证仿真精度。同时还可以识别载荷传递路径,为随机振动和振动疲劳问题求解提供条件。
结构动力学问题可以在时域或频域下求解。时域求解得到响应随时间的变化关系,在有限元软件中使用瞬态响应分析方法。频域求解得到响应随频率的变化关系,在有限元软件中使用频率响应分析方法(也有称谐响应分析)。频域求解还有一种方法叫响应谱分析,可以用来求解峰值响应,本文不在这方面做过多介绍。
频域的存在只是为了更容易表述和研究物理量随时间的变化规律。软件中描述的频率域下的物理量在实际空间中还是随时间变化的。相对于瞬态响应,频率响应分析结果我们都称为稳态响应。这句话表述很清楚,但并不那么容易理解。本文的写作目的就是通过一个案例来介绍结构动力学中瞬态响应与频率响应的关系。
1 模型描述
创建一个单自由度弹簧质量系统,一端全约束,另一端放开轴向移动约束,如下图所示。设置弹簧刚度与质量之比为3947.86,使系统共振频率恰好为10Hz。

2 频率响应分析
在5~15Hz范围内,求解幅值为1的正弦力作用下系统的加速度响应。仿真采用MSC Nastran的频率响应分析方法,其中模态阻尼比设置为0.1。激励和响应曲线如下所示,其中激励是力,响应是Y向加速度。

从频率响应结果曲线上可以看出,在10Hz附件响应最大,与系统固有频率重叠,准确反映出了系统的特性。
3 瞬态响应分析
为了探究频率响应曲线在每个频率点处具体的物理含义,先选定几个载荷频率分别计算系统的瞬态响应,然后通过瞬态响应结果解释频率响应结果的意义。载荷刚作用到系统上的短时间内,系统会有一个“适应”过程,之后会趋于稳定。如下所示,分别为载荷变化频率7.5Hz、10Hz和12.5Hz情况下的瞬态响应曲线。图中蓝色曲线是激励载荷的变化曲线,红色曲线是系统Y向加速度响应曲线。其中,激励载荷的幅值仍为1,模态阻尼比仍为0.1。
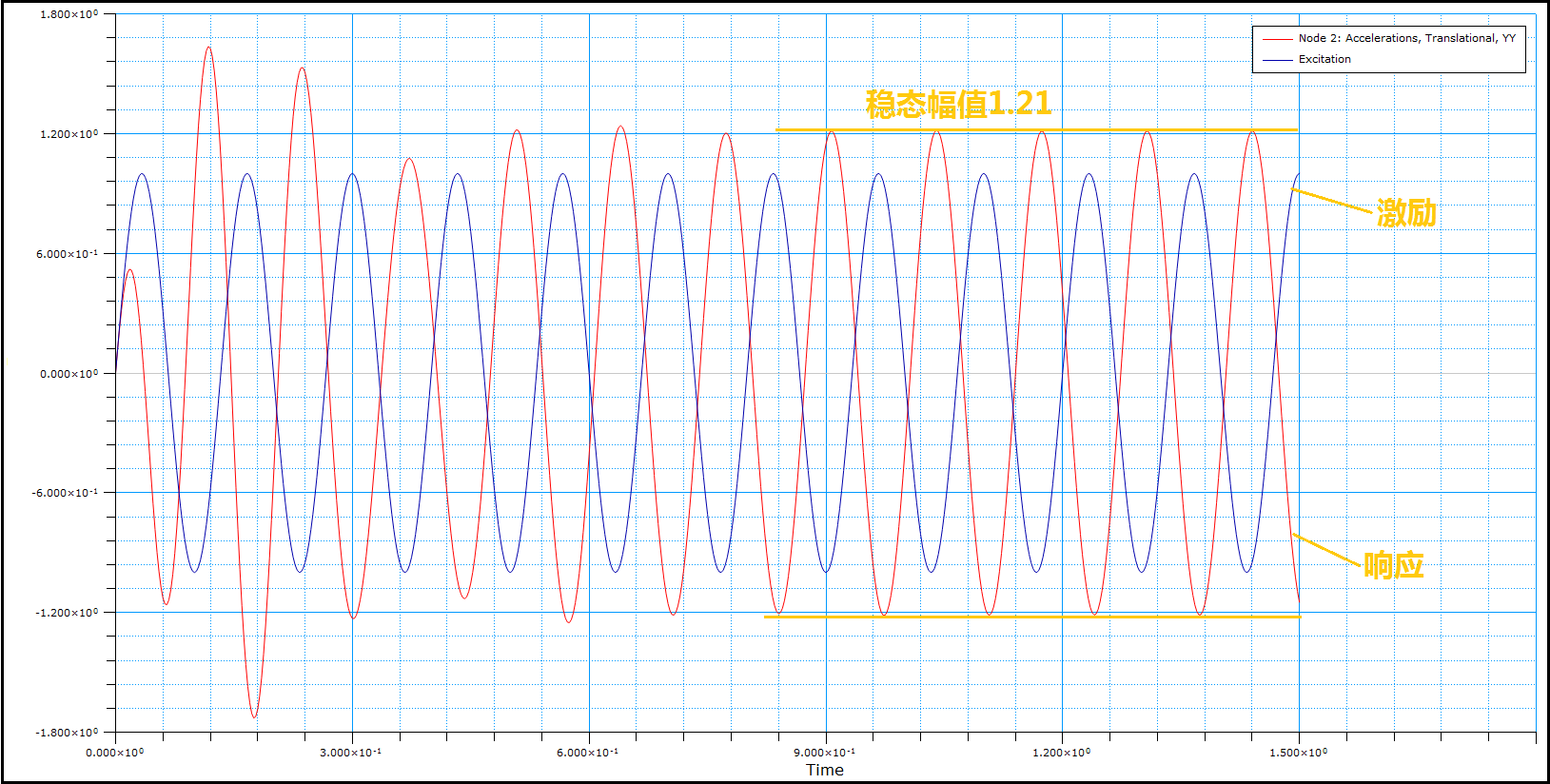
载荷频率7.5Hz
 载荷频率10Hz
载荷频率10Hz
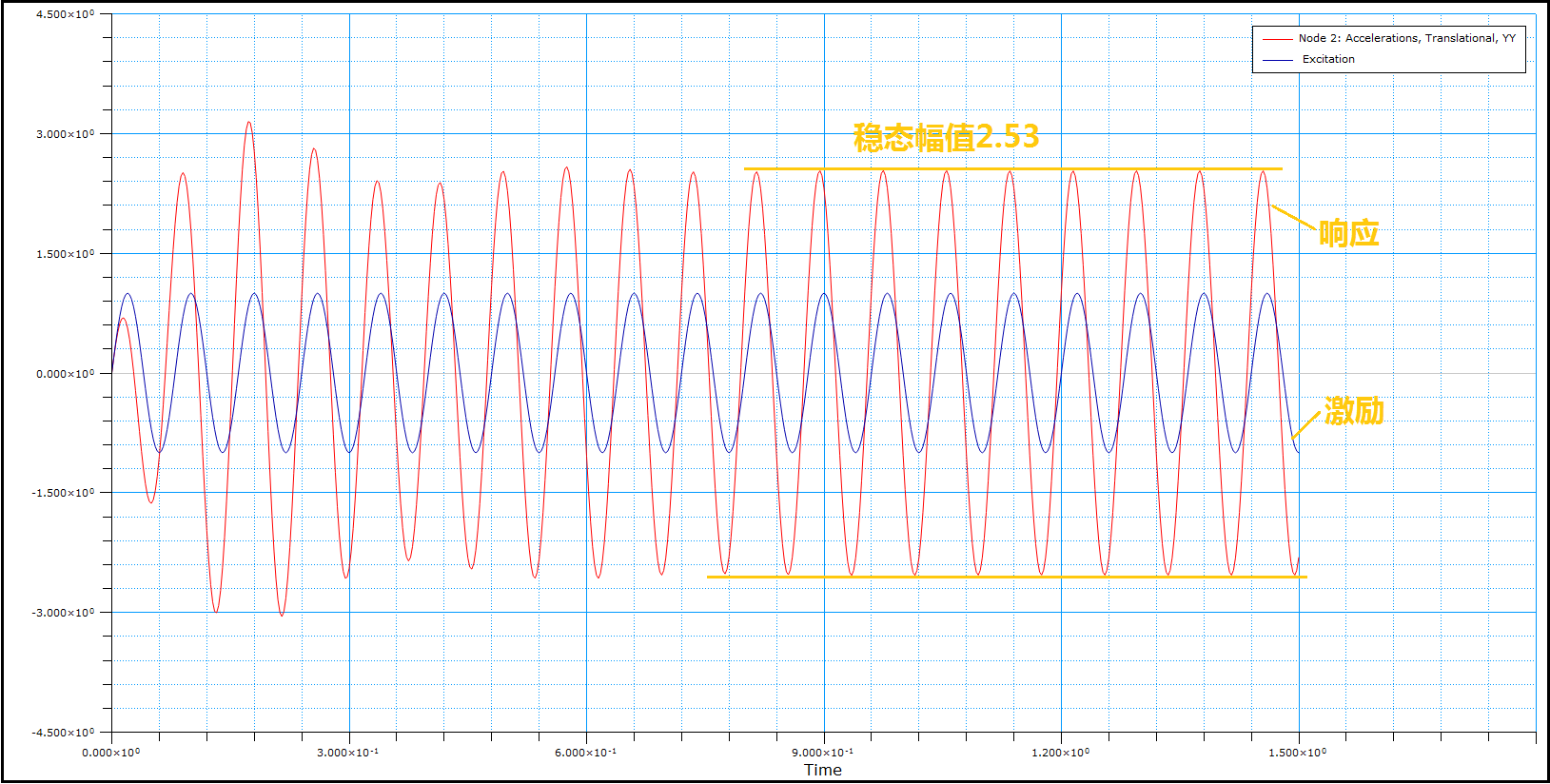 载荷频率12.5Hz
载荷频率12.5Hz
每个频率下,瞬态响应稳定后的幅值就可以叫做稳态响应。记录三个频率点下的加速度响应稳态幅值。
4 频率响应结果的意义
把瞬态响应分析中找到的稳态幅值叠加到频率响应曲线中,如下所示。
 瞬态响应结果与频率响应结果叠加
瞬态响应结果与频率响应结果叠加
从图中可以看出,瞬态响应的稳态幅值与对应频率点下的频率响应结果刚好吻合,这其实就解释了频率响应结果的物理意义。本例中频率响应输出101个点,每个频率的响应结果代表对应频率瞬态响应中稳定段的幅值。
确定的载荷作用到系统上,通过瞬态响应分析可以直接分析出任意时刻都确定的响应。但大多数情况下,我们对系统受到的载荷情况并没那么确定。这时候我们需要通过一种方法来判断系统可能的响应,频率响应分析方法恰好能起到这样的作用。需要注意的是频率响应结果给出的是受迫振动过程中的稳态响应,而非峰值响应。
通过频率响应分析可以反映出系统的固有振动特性,方便与试验对标,验证仿真精度。同时还可以识别载荷传递路径,为随机振动和振动疲劳问题求解提供条件。






